Доведення

За формулою (1.22) функція розподілу:

.

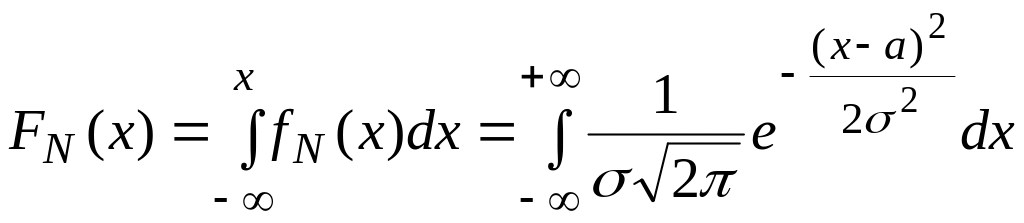Зробимо заміну змінної, позначивши , тоді та ,при , тому

.

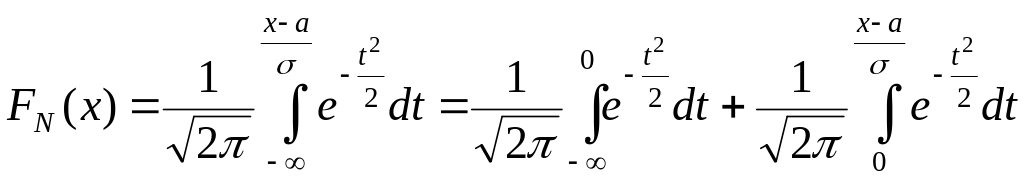Перший інтеграл

.

(в силу парності підінтегральної функції і того, що інтеграл Ейлера-Пуассона дорівнює ).

Оскільки 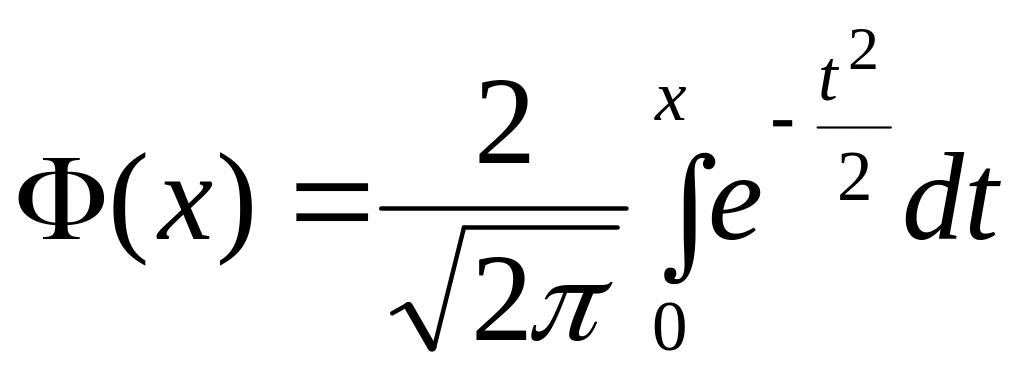, то другий інтеграл становить .

Тобто, .

З геометричної точки зору функція розподілу є площею під нормальною кривою на інтервалі (рис. 2.6). Очевидно, що вона складається з двох частин: на інтервалі вона дорівнює 0,5; на інтервалі – дорівнює .

Розглянемо основні властивості нормально розподіленої випадкової величини.

1. Ймовірність потрапляння випадкової величини , розподіленої за нормальним законом, в інтервал дорівнює

, (2.20)

де

, .

Доведення

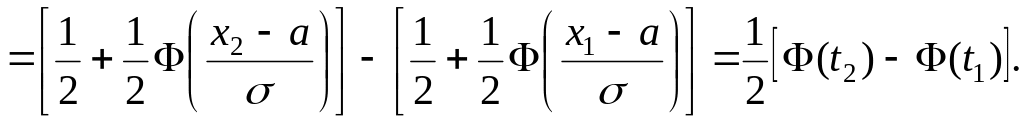
2. Ймовірність того, що відхилення випадкової величини , розподіленої за нормальним законом, від математичного сподівання не перевищить величину (за абсолютною величиною) дорівнює

, (2.21)

де

. (2.22)

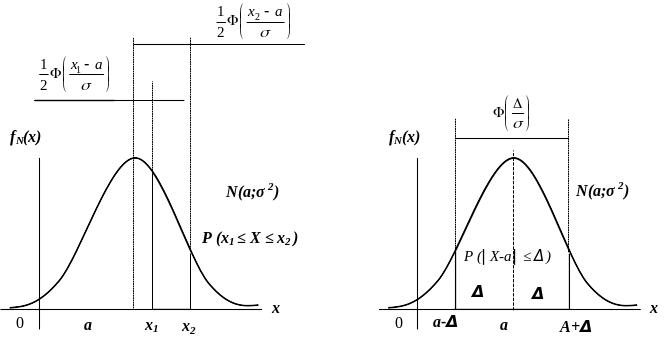На рис. 2.6 та 2.7 наведена геометрична інтерпретація властивостей нормального закону.

Рисунок 2.6 Рисунок 2.7

Обчислимо за формулою (2.21) ймовірності при різних значеннях . Маємо при

; (див. табл. А додатків)

;

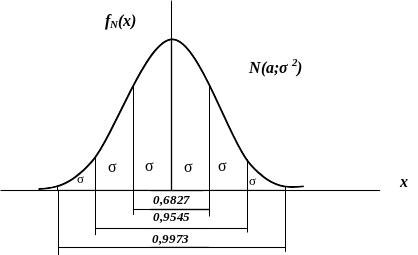
(рис. 2.8).

Звідси випливає "правило трьох сигм":

Якщо випадкова величина має нормальний закон розподілу з параметрами та , то практично достовірно, що її значення належать інтервалу .

Порушення "правила трьох сигм", тобто відхилення випадкової величини більше ніж на є подією практично неможливою, оскільки її ймовірність досить мала:

.

Рисунок 2.8

Знайдемо коефіцієнт асиметрії та ексцес випадкової величини , розподіленої за нормальним законом.

Зрозуміло, що в силу симетрії нормальної кривої відносно прямої , коефіцієнт асиметрії нормального розподілу . Тоді ексцес нормально розподіленої випадкової величини дорівнює

.

Приклад 2.8 Припускаючи, що зріст чоловіків певної вікової групи є нормально розподілена випадкова величина з параметрами та , знайти:

1. а) щільність ймовірності та функцію розподілу; б) частки костюмів 4-го зросту (176-182 см) та 3-го зросту (170-176 см), котрі потрібно передбачити в загальному обсязі виробництва для даної вікової групи; в) квантиль та 10%-ву точку випадкової величини .

2. Сформулювати "правило трьох сігм" для випадкової величини .

Розв’язування

1. а) За формулами (2.15) та (2.18) запишемо

;

.

б) Частка костюмів 4-го зросту в загальному обсязі виробництва обчислимо за формулою (2.20)

.

Аналогічно обчислюємо частку костюмів 3-го зросту

.

в) Квантиль знайдемо з рівняння (1.28) з врахуванням (2.19):

=0,7;

звідки

.

За таблицями А додатків знаходимо та

(см).

Це означає, що 70% чоловіків даної вікової групи мають зріст 176 см.

10%-ва точка випадкової величини – це квантиль см.

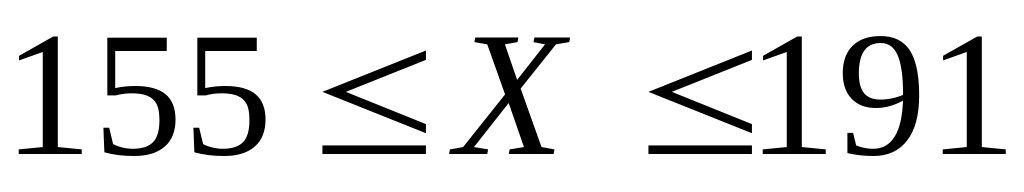2. Практично достовірно, що зріст чоловіків даної вікової групи знаходиться в межах від до (см), тобто (см).

Приклад 2.9 Випадкові похибки вимірювання мають нормальний закон розподілу ймовірностей із середнім квадратичним відхиленням =20мм і з математичним сподіванням а=0. Знайти ймовірність того, що із трьох незалежних вимірювань похибка хоч би одного не перевищуватиме за абсолютною величиною 4мм.