Элементарная статистическая

обработка результатов измерений.

1. Измерения. Классификация ошибок измерения.

1.1. Известно, что критерием истины является опыт, эксперимент. Опыт в естественных науках сопровождается измерениями определенных физических величин: массы, длины, времени, напряжения и т. д.

Измерить данную физическую величину – это значит сравнить ее с однородной ей величиной принятой за единицу.

1.2. Измерения бывают прямые и косвенные.

Прямое – это измерение физической величины непосредственно прибором, шкала которого проградуирована в единицах измерения этой величины. Например: измерение массы весами, длины – линейкой, тока – амперметром и т.д.

Косвенное измерение – это измерение, а точнее расчет искомой величины y через другие (x₁ x₂….. x_n), с которыми данная величина находится в определенной функциональной связи

y = y(x₁ x₂….. x_n)

Например. Плотность материала, из которого изготовлен параллелепипед, определяется по формуле

,

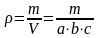где величина ρ функционально связана с величинами m,α,b,c.

1.3. Вся история развития естествознания показывает, что абсолютно точных измерений нет. При измерении всегда допускаются погрешности (ошибки). Иначе говоря, измеренное значение величины x отличается от неизвестного нам истинного a.

Отклонение измеренного значения от истинного называют абсолютной погрешностью (ошибкой) измерения

±x = (a - x) (1)

Знаки ± означают, что измеренное значение может быть меньше или больше истинного. Из записи (1) следует, что

a = Х ± Х (2)

Запись (2) означает, что реально при измерении мы можем определить не величину a , а интервал ее возможных значений

x - x ‹ a ‹ x + x

1.4 Очевидно, что чем меньше ошибка x, тем ближе измеряемое значение величины x к истинному. Однако сама по себе абсолютная ошибка не определяет точность, качество измерения. Так, ошибка x =1мм

при измерении длины стола будет незначительной; в то же время такая ошибка недопустима при измерении мелких деталей.

Точность измерения определяется относительной погрешностью, т.е. отношением абсолютной погрешности измерения данной величины к самой величине

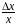
 = или  = ·100%.

Это величина безразмерная, но ее иногда выражают в %. Она удобна для сравнения точности измерения разнородных величин.

Пример: h =(102,5 ± 0,5)см ε = 0,5%

t = (5, 12 ± 0,05) с 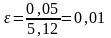ε = 1%

В примере измерение высоты в 2 раза точнее измерения времени.

1.5. Несмотря на разнообразие причин возникновения погрешностей при измерении, их можно разделить на три группы:

1. Промахи – это грубые погрешности, их появление - это результат неверного или небрежного измерения.

2. Систематические погрешности– это погрешности, обусловленные постоянно или закономерно действующими факторами в процессе измерения.

Причиной их являются несовершенство приборов, неверная методика измерений, пренебрежение к постоянно действующему внешнему фактору. Например: пренебрежение к силе Архимеда при взвешивании, изогнута стрелка прибора, сбито начало отсчета и т.д.

3. Случайные погрешности – это погрешности, обусловленные случайными факторами, действующими неодинаковым образом при каждом измерении.

Например: погрешности, обусловленные неверным положением глаз относительно указателя и шкалы прибора (ошибка параллакса); погрешности, вызываемые колебанием фундамента, конвекцией воздуха, температурными изменениями размеров, как объекта измерения, так и прибора и т.д.

Очевидно, что при измерении, прямом и косвенном надо учитывать все эти погрешности. Промахи будем обнаруживать и исключать при повторных измерениях (промахи значительно отличаются от остальных измерений), а вот систематические и случайные надо оценивать и суммировать. Чтобы их отличать, систематические будем обозначать значком ,,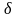 ^”- х, m, t и т.д. Случайные - значком „”- x‚ m, t и т.д.

2. Оценка систематической (приборной) погрешности прямого измерения.

Оценить приборную погрешность можно еще до измерения. Она указывается в паспорте прибора или на самом приборе. Если никаких указаний на этот счет в паспорте нет, то за абсолютную систематическую погрешность прибора берут половину цены деления (иногда цену деления) его шкалы.

х =

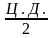
Цена деления шкалы – это значение наименьшего деления шкалы. Чтобы определить цену деления шкалы, нужно взять два любые (можно соседние) числа, из большего отнять меньшее, и результат разделить на число наименьших делений шкалы между этими числами.

3 4 5

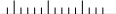Ц.Д. =

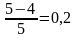
Часто, особенно в электроизмерительных приборах, приборная погрешность определяется классом точности. Он указан на шкале в виде числа 0,2 или 0.5 или 1,0 и т.д. (Всего классов точности восемь: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0).

Класс точности ε показывает, какую часть в процентах от максимального значения измеряемой величины составляет его приборная погрешность. Так, если мы имеем вольтметр с пределом измерения в 150В, а класс точности 0,5, то это значит, что приборная погрешность этого вольтметра

U = ε% ·U = 0, 5% · 150В = 0,75В

В заключении отметим, что прежде чем делать измерения любым прибором, надо обратить внимание на начальное положение указателя на ноль, если этого сделать нельзя (изогнута стрелка, стерто начало шкалы и т.д.), то во всю серию измерений следует вводить соответствующую поправку.

3. Оценка случайной погрешности прямого измерения.

Случайная погрешность, в отличие от систематической, проявляется только в процессе измерения и может быть выявлена и оценена в результате многократного измерения. Оценить случайную погрешность можно только статистически, т.е. методами теории вероятностей.

В теории вероятностей доказывается, что наилучшим результатом измерения величины a, является среднее арифметическое значение измерений этой величины x_ср.

Находится x_ср по результатам измерений:

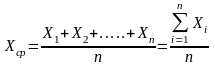
(1)

где n – число измерений величины x, а x₁, x₂,….,x_n результаты этих измерений.

Среднее арифметическое x_ср следует считать наилучшей оценкой неизвестного нам истинного значения измеряемой величины x.

Абсолютная погрешность отдельного измерения находится, как показано в пункте 1.3.

Среднее арифметическое из абсолютных значений погрешностей отдельных измерений называется средней абсолютной погрешностью измерения.

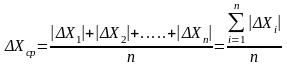(2)

Погрешности отдельных измерений берутся по модулю, т.к. при достаточно большом числе измерений случайные погрешности с равной вероятностью будут как в сторону преувеличения, так и в сторону преуменьшения измеряемой величины, т.е. как положительные, так и отрицательные, что в окончательном результате может дать ноль при нахождении суммы этих величин.

Если физическая величина измеряется один раз, то ее случайная погрешность будет равна нулю. Окончательный результат принято записывать следующим образом:

a = x_ср± x_ср (3)

Пример. Проведем 5 измерений длины ℓ некоторого предмета микрометром

с ценой деления Ц.Д.= 0,01мм.

Результаты измерений занесем в таблицу.

№ n/n	ℓi, мм	ℓi, мм
1	14,85	0.03
2	14,80	0,02
3	14,84	0,02
4	14,81	0,01
5	14,79	0,03
Ср.	14,82	0,02

В первом столбце записаны результаты пяти измерений (n =5). Среднее арифметическое находим по формуле (1) до разряда цены деления прибора:

ℓ_ср = 14,818мм = 14,82мм

Во втором столбце записаны отклонения среднего значения от каждого отдельного измерения(абсолютные погрешности каждого измерения). Среднюю абсолютную погрешность измерения определим по формуле (2): ℓ_ср = 0,02мм

Результат прямого измерения без учета систематической погрешности:

ℓ = ℓ_ср ± ℓ_ср = (14,82± 0,02)мм

С учетом систематической погрешности:

δℓ =

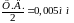
ℓ = ℓ_ср ± (ℓ_ср+δℓ) = 14,82 ±(0,02 +0,005) = 14,82±0,025 = (14,82 ±0,03)мм

4. Оценка систематической погрешности косвенного измерения.

Абсолютная погрешность косвенного измерения определяется через погрешности прямого измерения величин входящих в формулу по соответствующей ей расчетной формуле. Так, если

y = x₁ +x₂ +x₃ или y = x₁ – x₂ – x₃ , то

δy = (δx₁+ δx₂+ δx₃)

Т.е. погрешность суммы (или разности) равна всегда сумме погрешностей.

Сложнее найти формулу погрешности для других, более сложных функций. В этом случае дифференциальное исчисление позволяет воспользоваться следующим приемом:

1.Логарифмируем левую и правую части заданной формулы.

2.Дифференцируем полученный результат.

3.Знак дифференциала d заменяем знак погрешности δ и все слагаемые записываем со знаком „+”.

Пример.

1. lnρ = ln m - lnα -lnb -lnc

2.

3.

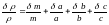
Зная относительную погрешность ε, можно найти абсолютную систематическую погрешность:

ε = 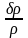, δρ = ε·ρ.

5. Оценка случайной погрешности косвенного измерения.

Случайная погрешность косвенного измерения определяется через случайные погрешности прямого измерения. Сначала определяется относительная погрешность косвенного измерения по правилу, изложенному в пункте 4, а затем – абсолютная (пример пункта 4).

ε = 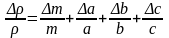, ρ = ε·ρ

При оценке окончательного результата измерений, как прямых, так и косвенных должны учитываться как систематическая (приборная), так и случайная погрешности. Однако, методика измерений, точность приборов и ряд других причин, могут оказаться таковыми, что одной из этих погрешностей можно пренебречь, в силу ее малости.

6. Запись результатов измерения.

Любые измерения являются приближенными. При записи приближенных чисел используются понятия о значащих цифрах и о верных и сомнительных цифрах числа. Значащими цифрами называются все цифры, полученные в результате прямого измерения. Исключением являются нули. Нули впереди не являются значащими. Число 0,0205 имеет три значащие цифры, а число 0,00020 всего только две. Нули в конце являются значащими, если они появились в результате измерения, а не перевода физической величины в другую систему единиц.

Так при измерении массы весами с ценой деления до 1мг получен результат: m = 79,900г. Здесь значащих цифр – 5. Нули в конце отбрасывать нельзя, т.к. запись m = 78,9г означала бы, что о следующих значащих цифрах после 9 нам ничего не известно, в то время как измерения показали, что они равны нулю.

Чем точнее прибор, тем больше значащих цифр, но оно всегда ограничено возможностями измерительного прибора (только точное число имеет неограниченное количество значащих цифр).

Верными значащими цифрами приближенного числа считаются все его цифры до того разряда, с которого начинается значащая цифра абсолютной погрешности этого числа: остальные значащие цифры будут сомнительными.

Например, при измерении времени t_ср= 23,08с, абсолютная погрешность оказалась равной t_ср= ± 0,06с. Здесь значащая цифра погрешности 6 начинается с сотых долей. Поэтому в числе верными будут цифры 2, 3, 0, а цифра 8 – сомнительная. Поэтому, приближенное значение измеряемой величины в большинстве случаев принято записывать до сомнительной цифры включительно, а абсолютную ее погрешность до одной значащей цифры, если она  1 и до двух значащих цифр, если первая равна 1.

При определении скорости движения получили значение _ср=0,5265 м/с, абсолютная погрешность при этом получилась равной _ср =0,011м/с.

Правильная запись результата:

 = _ср ± Δ_ср  = (0,527 ± 0,011) м/с,

но не имеет смысла записывать результат в виде:

 = ( 0,5265 ± 0,011) м/с или  = (0,5 ± 0,01) м/с

При определении линейных размеров правильная запись

ℓ = ( 64,53 ± 0,02) мм

будет неверной в виде ℓ = ( 64,5324 ± 0,02173) мм или

ℓ = (64,5 ± 0,02) мм или ℓ = (64, 532 ± 0,02) мм

Таким образом, приближенное число (результат измерения) и его абсолютная погрешность при записи должны быть цифрами одних и тех же разрядов.

Примеры. 1). Масса тела, полученная в результате эксперимента, равна:

m = 23, 67кг, случайная погрешность измерения составляет Δm = 0,054кг.

Правильная запись результата измерений:

m = (23, 67± 0,05)кг.

2). t = (3,768 ± 0,037)с = (3,77 ± 0,04)с.

3). S = (576,83 ± 3,037)м² =(577 ± 3)м².

4). I = (0,836 ± 0,017)A.

5). ℓ = (13,8 ± 0,087)м. В этом случае необходимо пересчитать величину ℓ до сотых значений, например ℓ = 13,83м, тогда окончательный результат запишем так: ℓ =(13,83 ± 0,09)м.

Графическое изображение результатов измерений.

Если некоторая физическая величина является функцией одной или двух переменных, то, для того чтобы получить наглядное изображение такой зависимости, бывает полезно изобразить ее графически. Для этого обычно используют прямоугольную систему координат.

Чтобы графически изобразить соответствующую зависимость, наносят на ось абсцисс шкалу значений аргумента, а на ось ординат шкалу значений функции. Например, зависимость температуры исследуемой жидкости от времени определяется функцией Т = f(t). Сравниваем полученную зависимость со стандартной математической зависимостью y = f(х), отсюда – функцию Т строим по оси у, а аргумент t – по оси х.

Результаты измерений, т.е. соответствующие пары значений аргумента (х) и функции (у), наносят на координатную плоскость в виде точек, а затем эти точки соединяют плавной линией.

Для построения графиков следует использовать специальную бумагу (миллиметровую). При их отсутствии иногда приходится (хотя это крайне нежелательно!) пользоваться бума­гой «в клеточку» или белой бумагой, на которой карандашом на­несена сетка.

При построении графиков следует разумно выбирать масшта­бы, чтобы измеренные точки располагались на всей площади листа. На рис. 1 изображены примеры правильного и неправиль­ного построения графика.

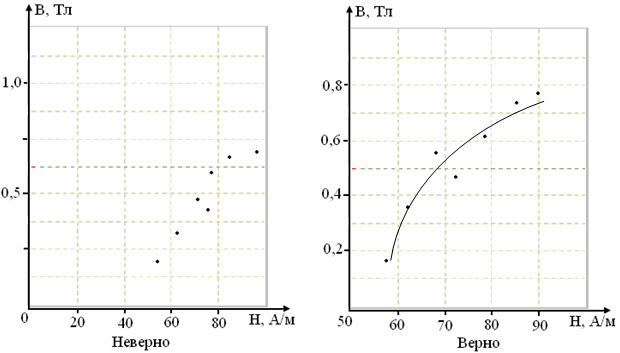
Рисунок 1.

На левом (неправильно построенном) графике экспериментальные точки занимают нижнюю правую часть рисунка. Чтобы этого избежать, следует выбрать более крупный масштаб по оси Y и сместить нуль на оси абсцисс, как это сделано на правом графике.

Масштаб должен быть удобным. Клеточка графика (или мил­лиметр миллиметровой бумаги) может соответствовать 0,1; 0,2; 0,5; 1; 2; 5; 10 и т. д. единицам измеряемой величины, но не 2,5; 3; 4; 7 и т. д.

Пример. Построить график зависимости . Сравниваем данный график со стандартным y= f(x). Величину откладываем по оси x, а величину по оси y.

Чтобы измеренные точки располагались на всей площади листа, выбираем наибольшее и наименьшее значения величины, из большего вычитаем меньшее и результат делим на удобное число.

Точки, наносимые на графики, должны изображаться четко и ясно. Их следует отмечать карандашом, так как иначе оши­бочно нанесенную точку нельзя удалить с графика, не испортив его. Никаких линий и отметок, поясняющих построение точек, на график наносить нельзя, так как они загромождают рисунок и мешают анализировать результаты.

Точки, полученные в разных условиях (при нагревании и при охлаждении, при увеличении и при уменьшении нагрузки, в раз­ные дни и т. д.), полезно наносить разными цветами или разны­ми значками. Это помогает увидеть новые явления. Так, графики рис. 2, а и 2, б изображают один и тот же набор точек. На рис. 2,а все эти точки нанесены одинаково, а на рис. 2, б точки, полученные при нагревании и охлаждении, изображены по-разно­му (точками и крестиками). На первом из графиков виден только разброс точек, а второй из них показывает, что разброс на самом деле невелик, но точки, измеренные при нагревании и при охлаж­дении, лежат на разных кривых. Ясно, что только рис. 2, б со­держит необходимую для анализа информацию и, следовательно, построен грамотно.

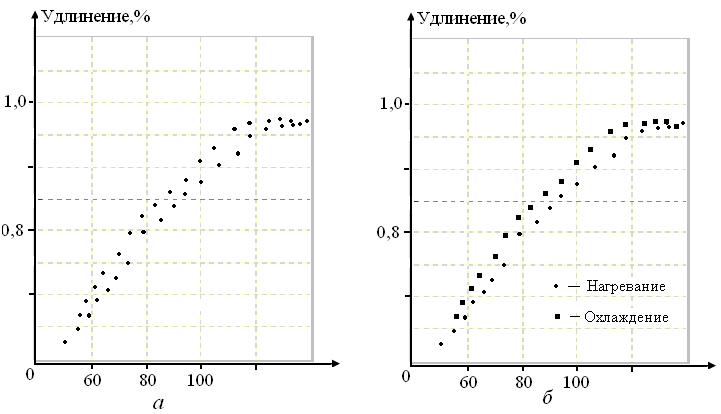
Рисунок 2.

При построении графиков соединять экспериментальные точки ломаной нельзя, поскольку в результате получается не график, а диаграмма. Линия графика должна быть плавной, но при этом совершенно не обязательно, чтобы она проходила через все экспериментальные точки, она должна быть плавной кривой с наименьшим числом перегибов, поскольку все, что мы знаем про истинный результат измерения, это то, что он наверное лежит где-то в каком-то интервале, который определяется погрешностью.

Через экспериментальные точки всегда следует проводить са­мую простую кривую, совместимую с этими точками.

При проведении кривой нужно следить за тем, чтобы на каж­дом достаточно большом ее участке экспериментальные точки располагались как выше, так и ниже кривой.

Измерительные приборы.

При выполнении лабораторных работ приходится пользоваться измерительными приборами. Рассмотрим устройство и принцип работы некоторых из них.

I. Приборы для измерения линейных размеров.

1. Штангенциркуль. Это прибор, который служит для линейных измерений, не требующих высокой точности. Он состоит из стальной штанги А (с неподвижной ножкой В) со шкалой, цена деления которой обычно равна 1мм. Вторая ножка Д подвижная имеет линейный нониус С.

Нониусом называется специальная шкала, дополняющая обычный масштаб и позволяющая повысить точность измерения в 10 – 20 раз.

Линейный нониус представляет собой небольшую линейку С, скользящую вдоль основной шкалы масштабной линейки. Когда ножки В и Д соприкасаются, нуль нониуса и основной шкалы совпадают (рисунок 1).

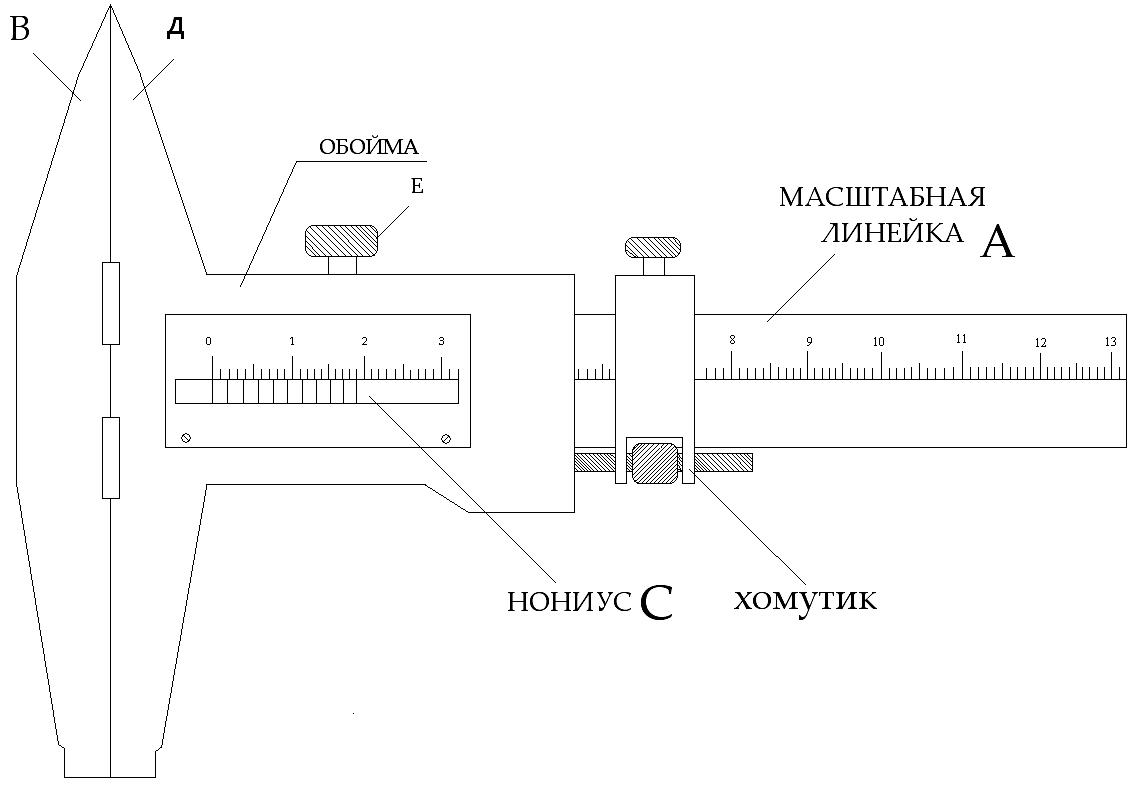
Рис. 1

Точность измерения штангенциркуля будет определяться точностью нониуса. Точность нониуса равна отношению цены деления шкалы масштабной линейки к числу делений на нониусе.

Чтобы измерить длину предмета, его помещают между ножками штангенциркуля В и Д, которые сдвигают до соприкосновения с предметом и закрепляют винтом Е. (рис 2). После этого делают отсчет по линейке и нониусу и вычисляют длину предмета.

Рис. 2

Для этого отсчитывают целое число миллиметров по линейке А, укладывающееся до нулевого деления нониуса. Затем по нониусу находят, какое по счету деление (риска) нониуса совпадает с делением (риской) линейной шкалы, умножают на точность нониуса и прибавляют к показаниям линейки.

Для рисунка 2 находим: точность нониуса равна: 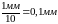; отсчет по линейке 16мм, отсчет по нониусу – (совпадает 7 –е деление нониуса с делением на основной шкале) 0,7мм. Таким образом, длина предмета 16,7мм.

При однократном или многократных измерениях в качестве систематической погрешности следует брать величину равную точности нониуса.

2. Микрометр.

Микрометр служит для более точных измерений линейных размеров. Основной частью его является микрометрический винт (рис.3), работа которого заключается в том, что линейное перемещение винта прямопропорционально величине его шага и углу поворота:

l =

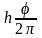
где l – линейное перемещение винта, φ – угол поворота винта в радианах,

h – шаг винта – смещение с барабана вдоль линейной шкалы за 1 оборот.

Микрометр состоит из скобы 1(рис.3), неподвижной пятки 2, вращающегося шпинделя 3 с микровинтом, стопорного винта 4 для закрепления шпинделя, гильзы 5 с основной линейкой 6, барабана 8 с круговой шкалой 7, колпачка 9 для крепления барабана на шпинделе и трещотки 10, служащей для равномерного нажатия шпинделя на измеряемый образец. Линейка 6 на гильзе 5 (рис.3), деления на которой нанесены через 1мм, представляет из себя две шкалы, сдвинутые друг относительно друга на 0,50мм (рис.4, а и б).

Верхняя шкала делит каждое деление нижней шкалы пополам. Микрометрический винт (рис.4, в) при вращении движется вдоль масштабной линейки и за один оборот передвигается на полделения, т.е. на 0,50мм. Барабан микрометрического винта разделен на 50 частей (рис.4, г), поэтому точность прибора определяется отношением, показанным на рисунке 4, т.е. получим 0,01 мм. Это указано на микрометре (рис.4, в).

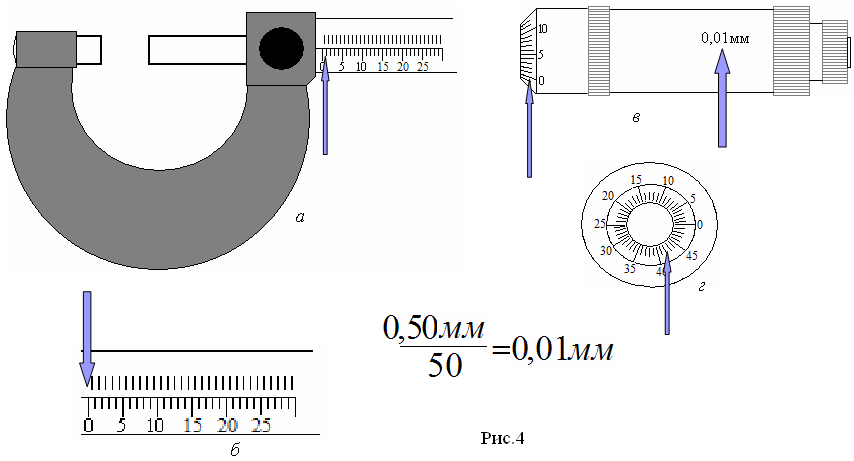
Измерения с помощью микрометра производятся в следующем порядке. Предмет помещают между пяткой 2 и шпинделем 3 и, вращая барабан при помощи трещотки 10, доводят шпиндель до упора о поверхность предмета, сигналом чего служат щелчки трещотки. По линейной шкале, против скошенного края барабана, отсчитывают целое число делений с точностью до 0,50мм. Десятые и сотые доли миллиметра отсчитывают по делению круговой шкалы, оказавшемуся против горизонтальной линии основной шкалы.

На рисунке 4 по линейной шкале целое число делений 11, по круговой шкале – 0,5, в итоге микрометр показывает значение 11,05мм.

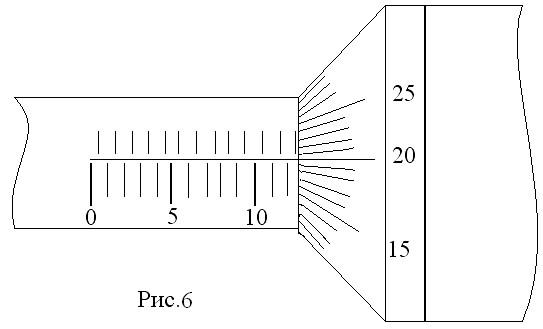
На рисунке 5 по линейной шкале целое число делений 12(на нижней части шкалы) и 0,5 деления (на верхней части шкалы), что составляет 12,50мм, по круговой шкале – 20 делений, это - 0,20мм. В результате, показания микрометра: 12,70мм (12+0,5+0,20).

Так как с помощью микрометра можно измерять с точностью до 0,01мм, то в качестве погрешности можно принять эту величину.

I I. Электроизмерительные приборы.

Электроизмерительными приборами называются приборы различных систем, измеряющие такие величины, как силу тока, напряжение, заряд, частоту тока, разность фаз, работу тока и т.д. Электроизмерительные приборы могут быть основаны на механическом перемещении подвижной части со стрелкой или зеркалом под действием электрических или электромагнитных сил. В зависимости от принципа действия этого устройства приборы делятся на магнитоэлектрические, электромагнитные, электродинамические и т.д. Эти системы электроизмерительных приборов различаются конструкцией, градуировкой шкалы, чувствительностью, точностью и т.д.

1. Приборы магнитоэлектрической системы.

Принцип действия приборов этой системы основан на взаимодействии измеряемого тока, протекающего по обмотке подвижной катушки, с магнитным полем постоянного магнита.

На рисунке показана схема устройства такого прибора. В зазоре 2 полюсных наконечников неподвижного постоянного магнита 1, изготовленного из высококоэрцитивной стали, устанавливается подвижная катушка (рамка) 3 из тонкого медного или алюминиевого провода, намотанного на легкий алюминиевый каркас, укрепленный на оси 00. Катушка представляет собой основную часть подвижной системы, которая включает и указатель – стрелку 4.

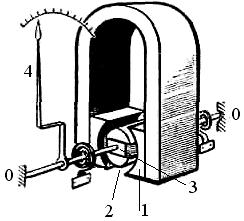При прохождении тока по виткам рамки возникает сила взаимодействия магнитных полей постоянного тока и постоянного магнита, образуя вращающий момент, пропорциональный силе тока. Вследствие этого взаимодействия подвижная часть прибора поворачивается на некоторый угол. Противодействующий момент создается пружинами, через которые подводится ток к рамке. Стрелка останавливается в таком положении, при котором вращающие моменты магнитных полей уравновешивающих вращающими моментами спиральных пружин, т.е. угол поворота стрелки оказывается пропорциональным силе тока, протекающего через прибор.

Приборы магнитоэлектрической системы применяются как вольтметры и амперметры постоянного тока. При этом клемма, отмеченная знаком „+”, подключается к клемме „+” источника э.д.с., а клемма „–” – на „–” источника.

2. Приборы электромагнитной системы.

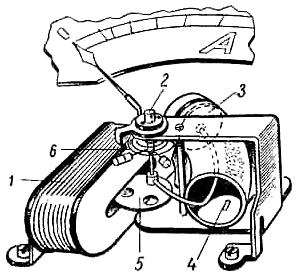
В приборах электромагнитной системы железный сердечник втягивается в катушку электромагнита при пропускании по ней тока. Такая конструкция прибора называется «с плоской катушкой». В амперметрах используется катушка с небольшим числом витков толстого провода, в вольтметрах – катушка с большим числом витков тонкого провода.

Плоский ферромагнитный сердечник 5 (с малой коэрцитивной силой) эксцентрично закреплен на оси 2. 3 – поршень воздушного демпфера (успокоителя), двигающегося в цилиндре 4.

Когда по катушке 1 проходит ток, сердечник втягивается в катушку, создавая вращающий момент, поворачивающий стрелку на некоторый угол. Противодействующий момент создается спиральной пружиной 6.

Приборы такой системы не реагируют на направление тока, давая отклонение всегда в одну сторону. Следовательно, им можно измерять как переменный, так и постоянный токи. Приборы просты по конструкции, устойчивы к перегрузкам, однако они менее точны, менее чувствительны, на их показания влияют внешние магнитные поля.

3. Приборы электродинамической системы.

В электродинамических приборах используются две катушки. Одна катушка (неподвижная) создает магнитное поле, другая вращается на оси, приводя в движение стрелку.

Механизм электродинамических приборов состоит из неподвижной катушки 1 и подвижной катушки 2, укрепленной на оси 4 внутри неподвижной.

В результате взаимодействия магнитных полей, созданных токами в подвижной и неподвижной катушках, возникает вращающий момент, пропорциональный произведению сил токов в этих катушках, под воздействием, которого подвижн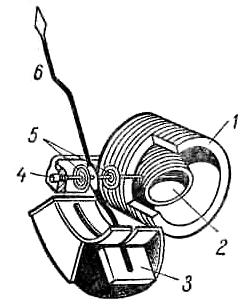 ая катушка и стрелка 6 поворачиваются на некоторый угол. Противодействующий момент создается пружинами 5. Демпфирование прибора воздушное с помощью крыльчатки 3.

Приборы электродинамической системы высокочувствительны и точны. Они предназначаются для измерения силы тока, напряжения и мощности в цепях постоянного и переменного токов. Чувствительность к перегрузкам, значительное влияние внешних магнитных полей – основные недостатки приборов этой системы.