
- •Санкт-Петербургский государственный горный университет Кафедра механики теория колебаний
- •Тема 1. Колебания материальной точки
- •Тема 2. Системы с одной степенью свободы
- •Тема 3. Системы с двумя степенями свободы
- •Контрольные вопросы:
- •Тема 4. Системы с несколькими степенями
- •Контрольные вопросы:
- •Тема 5. Системы с распределёнными параметрами
- •Тема 5. Нелинейные колебания
- •Контрольная работа
- •2.1. Теоретические основы работы
- •2.2. Пример выполнения ргр-2
- •1.2.1. Свободные колебания
- •1.3. Варианты заданий по ргр – 2
2.2. Пример выполнения ргр-2
Рассмотрим систему,
совершающую малые собственные колебания
около положения равновесия (рис.2.1).
Примем следующие обозначения элементов:
1 – груз массы
![]() ,
прикрепленный в точке А к свисающей
с блока нити; 2 – бицилиндр массы
,
прикрепленный в точке А к свисающей
с блока нити; 2 – бицилиндр массы
![]() с радиусами
с радиусами
![]() и радиусом инерции
и радиусом инерции
![]() относительно его геометрической оси;
3 – тонкий однородный стержень массы
относительно его геометрической оси;
3 – тонкий однородный стержень массы
![]() и длины
и длины
![]() ;
4 – блок массы
;
4 – блок массы
![]() (сплошной диск); 5 – каток массы
(сплошной диск); 5 – каток массы
![]() (сплошной однородный цилиндр); 6 –
стержень, массой которого можно
пренебречь.
(сплошной однородный цилиндр); 6 –
стержень, массой которого можно
пренебречь.
Пусть в системе
(рис.2.1) известны:
![]() = 5 кг,
= 5 кг,
![]() = 4 кг,
=1 кг,
= 8 кг,
= 4 кг,
=1 кг,
= 8 кг,
![]() = 0,04 м,
= 0,04 м,
![]() = 0,08 м,
= 0,06 м,
=0,45 м, а также коэффициент жесткости
пружины
= 0,08 м,
= 0,06 м,
=0,45 м, а также коэффициент жесткости
пружины
![]() =2400 Н/м, начальное отклонение груза
1 по вертикали от положения его статического
равновесия
=2400 Н/м, начальное отклонение груза
1 по вертикали от положения его статического
равновесия
![]() = 0,003 м и проекция начальной скорости
груза на вертикальную ось
= 0,003 м и проекция начальной скорости
груза на вертикальную ось
![]() = 0,03м/с. Примем
= 10 м2/с.
= 0,03м/с. Примем
= 10 м2/с.
Найти уравнение движения груза при заданных начальных условиях, амплитуду, частоту, период его колебаний и построить графики колебаний для свободных и затухающих колебаний.
Рис. 2.1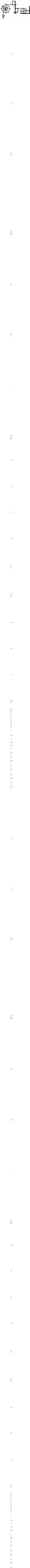
1.2.1. Свободные колебания
Система имеет одну
степень свободы (рис.2.1). За обобщенную
координату примем вертикальное отклонение
![]() груза 1 от положения статического
равновесия вниз. Все задаваемые силы,
приложенные к системе, имеют потенциал,
поэтому уравнение Лагранжа можно
записать в форме (2.7).
груза 1 от положения статического
равновесия вниз. Все задаваемые силы,
приложенные к системе, имеют потенциал,
поэтому уравнение Лагранжа можно
записать в форме (2.7).
Кинетическая энергия всей рассматриваемой системы
![]() .
(2.18)
.
(2.18)
Груз 1 движется поступательно, следовательно, его кинетическая энергия равна
![]()
где
![]() - неизвестная скорость перемещения
груза 1, равная обобщенной скорости
- неизвестная скорость перемещения
груза 1, равная обобщенной скорости
![]() .
.
Бицилиндрический
блок 2 вращается вокруг неподвижной оси
![]() с угловой скоростью
с угловой скоростью
![]() .
Радиус инерции блока известен, поэтому
.
Радиус инерции блока известен, поэтому
![]() .
Кинетическая энергия бицилиндра:
.
Кинетическая энергия бицилиндра:
 .
.
Стержень 3 вращается
вокруг неподвижной оси
![]() ,
тогда кинетическая энергия равна
,
тогда кинетическая энергия равна
![]() .
Момент инерции стержня относительно
оси, проходящей через его конец, известен:
.
Момент инерции стержня относительно
оси, проходящей через его конец, известен:
![]() .
Для нахождения угловой скорости
.
Для нахождения угловой скорости
![]() стержня рассмотрим точки В и С,
которые движутся практически с одинаковыми
скоростями (вследствие малости
рассматриваемых колебаний). Тогда
стержня рассмотрим точки В и С,
которые движутся практически с одинаковыми
скоростями (вследствие малости
рассматриваемых колебаний). Тогда
![]() .
Отсюда искомая угловая скорость
.
Отсюда искомая угловая скорость
![]() .
Таким образом, кинетическая энергия
стержня 3 равна
.
Таким образом, кинетическая энергия
стержня 3 равна
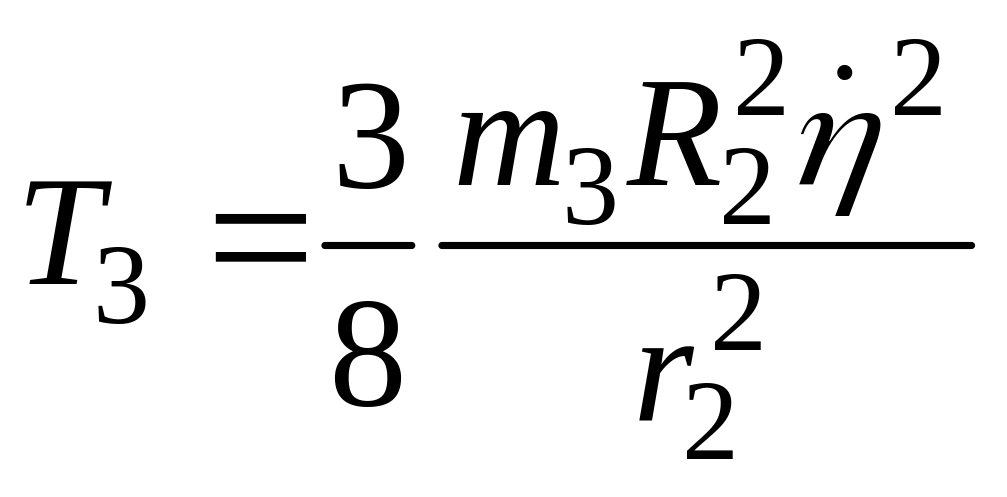 .
.
Каток 5 совершает
плоскопараллельное (плоское) движение,
состоящее из поступательного движения
вместе с полюсом О2 и вращательного
движения вокруг последнего. Поэтому
кинетическая энергия этого катка:
![]() ,
где
,
где
![]() - кинетическая энергия поступательного
движения;
- кинетическая энергия поступательного
движения;
![]() - то же для вращательной части плоского
движения.
- то же для вращательной части плоского
движения.
Мгновенный центр
скоростей (МЦС) катка находится в точке
Р, поэтому угловая скорость катка
![]() определяется как отношение скорости
точки Е к длине диаметра ЕР:
определяется как отношение скорости
точки Е к длине диаметра ЕР:
![]() ,
где
,
где
![]() - радиус катка 5. Скорость
- радиус катка 5. Скорость
![]() ,
тогда
,
тогда
![]() .
Для нахождения кинетической энергии
Тп определим скорость
поступательного движения катка
.
Для нахождения кинетической энергии
Тп определим скорость
поступательного движения катка
![]() .
С учетом этого имеем:
.
С учетом этого имеем:
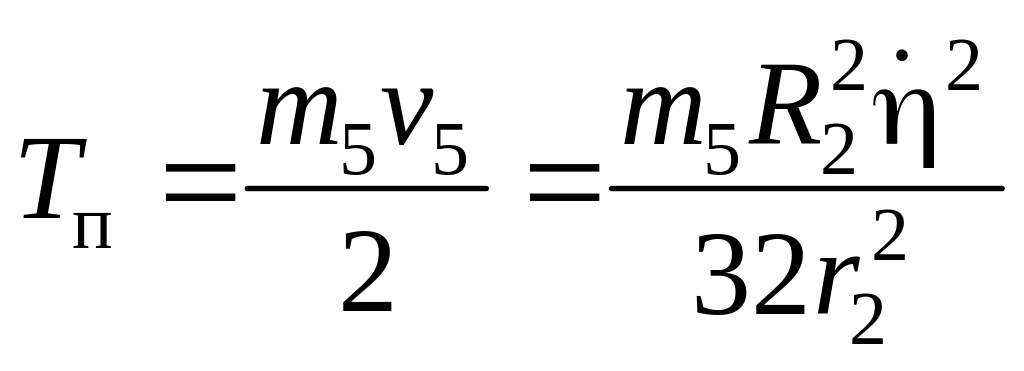 .
.
Теперь найдем
![]() ,
где
,
где
![]() - момент инерции катка 5 относительно
МЦС (точка Р). Как известно,
- момент инерции катка 5 относительно
МЦС (точка Р). Как известно,
![]() ,
где
,
где
![]() - момент инерции катка 5 относительно
его центра тяжести (точка О2):
- момент инерции катка 5 относительно
его центра тяжести (точка О2):
![]() .
С учетом последнего имеем:
.
С учетом последнего имеем:
![]() .
Тогда кинетическая энергия будет равна:
.
Тогда кинетическая энергия будет равна:
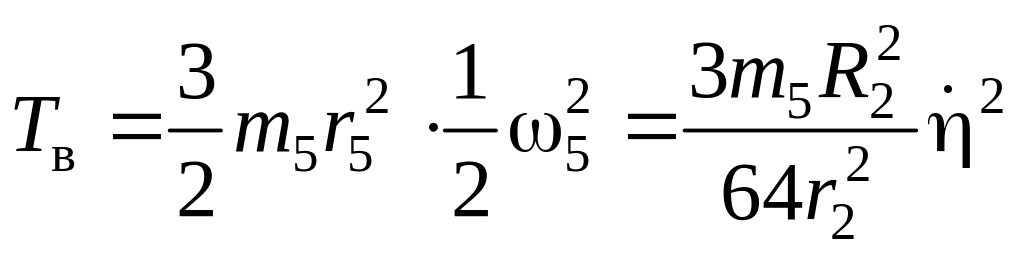 .
.
Теперь полная кинетическая энергия катка определится следующим образом:
![]() .
.
В соответствии с формулой (1.18) кинетическая энергия рассматриваемой системы будет равна
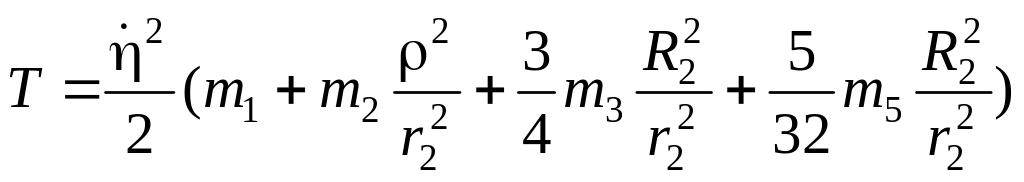 .
.
Выражение, стоящее
в скобках, назовем приведенной массой
системы и обозначим
.
Причем
![]() .
Вычислим приведенную массу для нашего
случая
.
Вычислим приведенную массу для нашего
случая
![]() кг.
кг.
В результате
получим для кинетической энергии всей
системы:
![]() .
.
Потенциальная энергия системы определяется работой сил тяжести системы и силы упругости пружины на перемещении системы из отклоненного положения, когда груз 1 имеет координату , в положение статического равновесия. При таком отклонении вес блока и вес катка работы не производят, поэтому потенциальная энергия всей системы равна
![]() , (2.19)
, (2.19)
где
![]() - потенциальная энергия пружины.
- потенциальная энергия пружины.
Очевидно, что
![]() .
Знак минус ставится потому, что груз 1
из положения статического равновесия
отклоняется вниз при положительном
.
Точно также (см. рис.2.2)
.
Знак минус ставится потому, что груз 1
из положения статического равновесия
отклоняется вниз при положительном
.
Точно также (см. рис.2.2)
![]() ;
из рис.1.2 видно, что
;
из рис.1.2 видно, что
![]() .
.
Поскольку
рассматриваются малые колебания системы,
угол
![]() весьма мал и, следовательно, синус в
последнем выражении можно заменить
непосредственно углом. Тем самым в
разложении синуса в ряд сохраняется
лишь один член. В теории малых колебаний
большая точность не нужна, ибо потенциальную
энергию необходимо вычислять с точностью
до величин второго порядка малости
относительно обобщенной координаты.
весьма мал и, следовательно, синус в
последнем выражении можно заменить
непосредственно углом. Тем самым в
разложении синуса в ряд сохраняется
лишь один член. В теории малых колебаний
большая точность не нужна, ибо потенциальную
энергию необходимо вычислять с точностью
до величин второго порядка малости
относительно обобщенной координаты.
Таким образом,
имеем
![]() .
Для нахождения угла
.
Для нахождения угла
![]() воспользуемся формулой
воспользуемся формулой
![]() .
Смещение
.
Смещение
![]() с принятой точностью совпадает с
перемещением точки, лежащей на поверхности
блока, т.е.
с принятой точностью совпадает с
перемещением точки, лежащей на поверхности
блока, т.е.
![]() .
Тогда
.
Тогда
 .
.
Следовательно,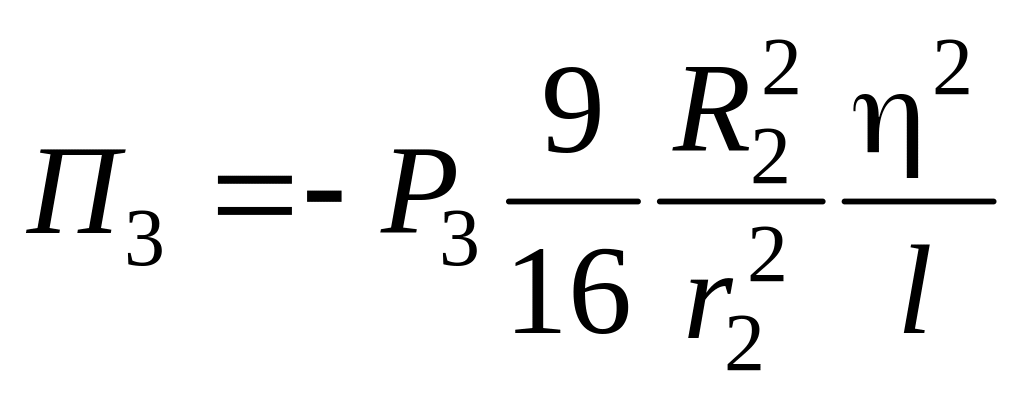 .
.
Потенциальная энергия пружины
![]() ,
,
где
![]() - перемещение точки
- перемещение точки
![]() из положения, соответствующего условию
из положения, соответствующего условию
![]() ;
- статическая деформация пружины.
;
- статическая деформация пружины.
Перемещение вдвое меньше смещения точки Е, которое, в свою очередь, равно перемещению точки D. Таким образом, имеем
![]() .
.
После несложных преобразований получим
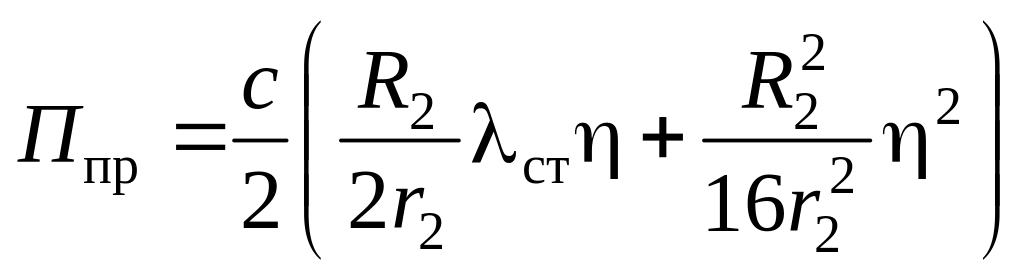 .
.
С учетом выражения (2.19) получаем выражение для определения потенциальной энергии всей системы
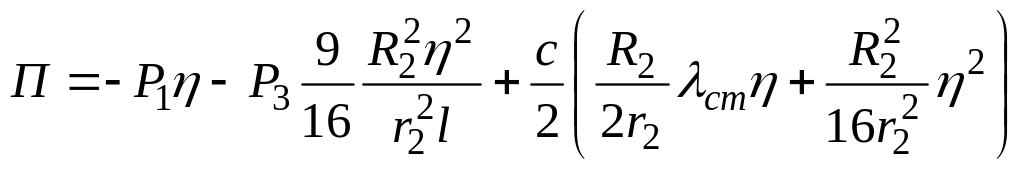 .
(2.20)
.
(2.20)
В положении, соответствующем , система находится в равновесии, поэтому должно выполняться условие:
![]() .
.
Тогда из (2.9) получаем
![]() .
(2.21)
.
(2.21)
Отсюда можно найти статическую деформацию пружины. С помощью формулы (1.10) выражение (1.9) упрощается и принимает вид
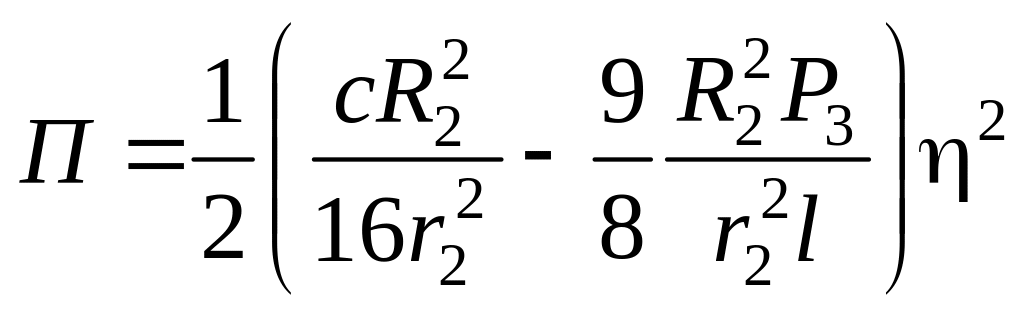 .
(2.22)
.
(2.22)
Выражение в скобках
в (1.22) обозначим
![]() и назовем квазиупругим коэффициентом.
Заметим, что
и назовем квазиупругим коэффициентом.
Заметим, что
![]() .
После вычислений получим, что
рассматриваемом случае квазиупругий
коэффициент равен
.
После вычислений получим, что
рассматриваемом случае квазиупругий
коэффициент равен
![]() Н/м.
Н/м.
Таким образом, потенциальная энергия системы равна
![]() .
.
Для использования уравнения Лагранжа необходимо найти производные от кинетической и потенциальной энергий:
![]() .
(2.23)
.
(2.23)
Подставляя (1.23) в формулу (1.7), получим
![]() ,
(2.24)
,
(2.24)
где
![]() рад/с;
рад/с;
![]() с;
с;
![]() Гц.
Гц.
Решением уравнения (1.24) при известном значении k будет
![]() см
см
или, согласно выражению (2.12),
![]() см.
(2.25)
см.
(2.25)
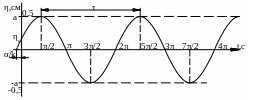 График
свободных колебаний системы, согласно
закону (2.25), приведены на рис.2.3.
График
свободных колебаний системы, согласно
закону (2.25), приведены на рис.2.3.
Рис.2.3
