10 семестр / Книги и методические указания / Метода

Московский государственный технический университет имени Н.Э. Баумана

А.С. Ющенко, Д.С. Делия

СТАТИСТИЧЕСКИЙ АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Методические указания к лабораторному практикуму по курсу «Статистическая динамика систем автоматического управления»

Под редакцией А.С. Ющенко

М о с к в а

Издательство МГТУ им. Н.Э. Баумана

2 0 0 9

УДК 519.711.3 ББК 22.161.6 Ю985

Рецензент д-р техн. наук, проф. В.С. Медведев

Ющенко А.С., Делия Д.С.

Ю985 Статистический анализ линейных систем автоматического управления: Метод. указания к лабораторному практикуму по курсу «Статистическая динамика систем автоматического управления» / Под ред. А.С. Ющенко. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. — 52 с.: ил.

В работе приведено описание трех лабораторных работ по курсу «Статистическая динамика систем автоматического управления» с использованием ПЭВМ и пакета MATLAB 7, посвященных формированию случайных процессов с заданными характеристиками, анализу линейной непрерывной автоматической системы при воздействии на нее случайного процесса и исследованию автоматической системы при воздействии на нее случайного сигнала и помехи. Методические указания содержат необходимые математические формулы, сведения о пакете MATLAB 7, необходимые при проведении лабораторных работ, а также примеры проведения исследований.

Для студентов старших курсов, обучающихся по направлениям подготовки 220400 «Мехатроника и робототехника» и 220200 «Управление в технических системах».

УДК 519.711.3 ББК 22.161.6

Учебное издание

Ющенко Аркадий Семенович Делия Данила Сергеевич

СТАТИСТИЧЕСКИЙ АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Редактор С.А. Серебрякова Корректор М.А. Василевская

Компьютерная верстка С.А. Серебряковой

Подписано в печать 16.12.2008. Формат 60×84/16. Бумага офсетная.

Усл. печ. л. 3,02. Уч.-изд. л. 2,83.
Изд. № 148. Тираж 200 экз. Заказ	.

Издательство МГТУ им. Н.Э. Баумана Типография МГТУ им. Н.Э. Баумана 105005, Москва, 2-я Бауманская ул., 5

© МГТУ им. Н.Э. Баумана, 2009

ВВЕДЕНИЕ

Данное пособие предназначено для самостоятельного проведения студентами цикла лабораторных работ по курсу «Статистическая динамика систем автоматического управления» на ПЭВМ с использованием программного пакета MATLAB. Такой курс предусмотрен в учебном плане ряда специальностей, связанных с автоматизацией, мехатроникой и робототехникой. Предполагается, что студенты знакомы с основным курсом теории автоматического управления и с теорией вероятностей. Для того чтобы облегчить проведение лабораторных работ, в методических указаниях даны основные соотношения из курса «Статистическая динамика систем автоматического управления», которые используются при статистическом анализе линейных стационарных автоматических систем. Приведено краткое описание возможностей пакета MATLAB 7 для проведения такого анализа.

В пособии даны указания к проведению трех лабораторных работ, объединенных в общий цикл. Вначале нужно построить формирующий фильтр, позволяющий получить случайный процесс с заданными статистическими характеристиками. Затем провести исследование системы, на вход которой поступают детерминированный сигнал и случайная помеха. Наконец, предлагается исследовать замкнутую систему автоматического регулирования, ко входу которой приложен случайный сигнал, представляющий собой аддитивную смесь полезного случайного сигнала и случайного шума. Описание каждой лабораторной работы сопровождается примерами. Для того чтобы правильно интерпретировать получаемые результаты, мы рекомендуем предварительно выполнить статистическое исследование в аналитической форме с использованием приведенных в пособии соотношений. Более подробную информацию о методах статистического анализа автоматических систем и о возможностях пакета MATLAB можно найти в литературе, список которой приведен в конце пособия [1 – 4].

3

1. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ СООТНОШЕНИЯ, ИСПОЛЬЗУЕМЫЕ ПРИ СТАТИСТИЧЕСКОМ АНАЛИЗЕ АВТОМАТИЧЕСКИХ СИСТЕМ

1.1. Характеристики случайных процессов

Основными характеристиками случайных величин являются функция распределения вероятности и плотность распределения вероятности. Функция распределения случайной величины ξ, принимающей любые вещественные значения, определяется соотношением

Fξ (x) = P{ξ < x}

(1)

и представляет собой вероятность того, что случайная величина ξ принимает значения, меньшие заданного значения x.

Плотность распределения вероятности случайной величины ξ может быть определена по функции распределения вероятности с использованием формулы

dFξ (x)

pξ (x) = . (2) dx

Случайный процесс определяется множеством случайных реализаций ξ(t), 0 ≤ t ≤ T. Фиксируя произвольным образом моменты времени ti, i = 1, 2, …, N, можно получить N-мерную случайную величину ξ = [ξ(t1), ξ(t2),…,ξ(tN)], т. е. случайный вектор, компонентами которого являются случайные величины, представляющие собой значения реализаций ξ(t) в дискретные моменты времени. Таким образом, случайный процесс характеризуется множеством функций распределения вероятности, определяющих векторную случайную величину ξ:

4

Fξk (x1, x2 ,..., xk ,t1, t2 ,...,tk ) = P{ξ(t1 ) < x1, ξ(t2 ) < x2 , ..., ξ(tk ) < xk }, (3)

где k = 1, 2, …, N, или соответствующим множеством плотностей распределения вероятности:

pξk ( x1 , x2 , ..., xk , t1 , t2 , ..., tk ) =

	∂ k
=		Fξk (x1 , x2 , ..., xk , t1 , t2 , ..., tk ), (4)
	∂x1∂x2 ...∂xk

где k = 1, 2, …, N.

Используя плотности распределения вероятности, можно определить моменты различного порядка для случайного процесса ξ(t). Наиболее часто применяют начальный момент первого порядка (математическое ожидание):

∞
mξ (t) = M{ξ(t)} = ∫ xpξ1(x,t)dx	(5)

−∞

и центральный момент второго порядка (корреляционную (автокорреляционную) функцию):

Kξ (t1, t2 ) = M{ξ(t1) ξ(t2 )} =

∞ ∞

=∫ ∫ ( x1 − mξ (t1))(x2 − mξ (t2 )) pξ2 (x1, x2 , t1, t2 )dx1dx2. (6)

−∞ −∞

Из последнего выражения можно также найти дисперсию случайного процесса:

Dξ (t) = M{ξ(t) ξ(t)}.	(7)

Взаимнокорреляционную функцию двух случайных процессов ξ(t) и η(t) определяют по формуле

Kξη(t1,t2) = M{ξ(t1)η(t2)} =

∞ ∞
= ∫ ∫ (x1 −mξ(t1))(x2 −mξ(t2)) pξη2(x1, x2,t1,t2 )dx1dx2.	(8)

−∞−∞

5

Напомним, что случайный процесс ξ(t) называется стационарным (в широком смысле), если его математическое ожидание постоянно, а корреляционная функция зависит только от разности аргументов:

mξ (t) = mξ = const ,	(9)
Kξ(t1,t2) = Kξ(t1 −t2) = Kξ (τ).	(10)

Для стационарных процессов можно определить спектральную плотность случайного процесса как преобразование Фурье корреляционной функции:

∞
Sξ (ω) = ∫ Kξ (τ)e− j ωτdτ.	(11)

−∞

По заданной спектральной плотности можно определить корреляционную функцию:

1		∞
		∫	Sξ	(ω)e j ωτdω.	(12)
	2π
Kξ (τ) =

−∞

Из последней формулы следует и выражение для вычисления дисперсии стационарного случайного процесса по его спектральной плотности:

	1		∞
Dξ = Kξ (0)	=		∫	Sξ	(ω)dω.	(13)
		2π

−∞

При статистической обработке случайных сигналов используются методы и формулы математической статистики.

Пусть на интервале времени [0, T] экспериментально получено n реализаций случайного процесса ξ(t), которые мы обозначим xi(t), i = 1, 2, …, n. Тогда оценка математического ожидания случайного процесса может быть определена по формуле

			1	n
	mˆ ξ	(t) =		∑xi (t).	(14)
			n i =1
	Оценка (14) является несмещенной, т. е. M{mˆξ} = mξ ,				и состоя-
	тельной, поскольку выполняется условие lim D{mˆξ} = 0.
				n→∞
	6

Вычислив оценку математического ожидания случайного процесса, можно найти оценку его автокорреляционной функции по формуле

1

n

ˆ

(t1, t2 )

=

∑(xi

(t1)

−

mˆ ξ

(t1))(xi (t2 )

−

mˆ ξ

(t2 )).

(15)

Kξ

n −1 i =1

Здесь используется множитель

1

, а не

1

, чтобы обеспечить

n −1

n

несмещенность оценки (15). Ее состоятельность, как и состоятельность оценки математического ожидания, можно легко проверить.

Для оценки дисперсии из последней формулы получим:

			1	n
ˆ		=		∑(xi		−	mˆ ξ	2
	(t)				(t)			(t))	.	(16)
Dξ
			n −1 i =1

При исследовании статистических характеристик стационарных случайных процессов часто применяют эргодическую гипотезу, позволяющую существенно упростить их вычисление. В этом случае вместо усреднения значений множества реализаций в одни и те же моменты времени, как в формулах (14) – (16), усредняют значения одной реализации, взятые в различные моменты времени.

Стационарный процесс называется эргодическим по отношению к математическому ожиданию, если является несмещенной и состоятельной следующая статистическая оценка математического ожидания, определяемая по одной его реализации x(t), измеряемой на интервале времени [0; T]:

	mˆ ξ =	1	T	x(t)dt.	(17)
		T	∫
			0

Эта оценка является несмещенной и состоятельной, если выпол-

няются условия M{mˆξ} = mξ и lim D{mˆξ} = 0. Нетрудно непосред-

n→∞

ственно убедиться в несмещенности оценки (17). Для ее состоятельности нужно дополнительно потребовать, чтобы выполнялось условие

lim Kξ (τ) = 0.	(18)
τ→∞
	7

Смысл последнего условия состоит в том, что значения случайных величин ξ(ti) и ξ(tj) становятся слабо коррелированными при увеличении временного интервала (tj – ti).

Для практических расчетов по формуле (17) используют приближенное соотношение

			1	N
	mˆ ξ	=		∑x(ti ).	(19)
			N +1 i =0

В частности, если интервал [0; T] разбит на N элементарных интервалов длиной t = T/N, то ti = i t, i = 0, 1, …, N. Можно также записать, что N = T/ t = Tfd, где fd = 1/ t — частота дискретизации, Гц.

Рассмотрим теперь оценку корреляционной функции стационарного случайного процесса:

Kξ (τ) = M{(ξ(t) − mˆ ξ )(ξ(t + τ) − mˆ ξ )}.

(20)

Обозначив x(t) отдельную реализацию случайного процесса и принимая во внимание, что интервал, на котором происходит вычисление оценки корреляционной функции, равен [0; T – τ], получим следующую формулу для оценки корреляционной функции:

		1		T − τ
ˆ				∫	( x(t) − mˆ ξ )( x(t + τ) − mˆ ξ )dt,
Kξ	(τ) =	T − τ
				0
или
				1		T −τ
	ˆ					∫	2
	Kξ	(τ) =	T − τ				x(t)x(t + τ)dt − mˆ ξ .
						0

(21)

(22)

Эти оценки являются несмещенными, а для их состоятельности достаточно выполнения условия (18). В этом случае стационарный случайный процесс ξ(t) называется эргодическим по отношению к корреляционной функции. Вычисление корреляционной функции как среднего по множеству в формуле (20) можно приближенно заменить вычислением среднего по времени согласно формуле (21) или (22). В частности, при τ = 0 отсюда можно получить оценку для дисперсии эргодического процесса:

ˆ =

1

T

−

2

=

1

T

2

− 2

Dξ

T

∫

( x(t)

mˆ ξ )

dt

T

∫

x

(t)dt

mˆ ξ .

(23)

0

0

8

На практике оценку корреляционной функции обычно вычисляют по дискретным значениям реализации случайного процесса ξ(ti). В этом случае вместо (21) используют следующую формулу:

ˆ					1		N −m
	(m) =						∑ (x(ti ) − mˆ ξ )(x(ti+m) − mˆ ξ ),
Kξ											(24)
		N		− m +1 i=0
где m = 0, 1, 2, …, N,				N = T/ t = Tfd.
Из последней формулы при m = 0 получим оценку дисперсии и
стандартного (среднего квадратического) отклонения:
				1		N
	ˆ					∑( x(ti ) − mˆ ξ )		2		ˆ
	Dξ =								,	σˆ ε = Dε .	(25)
			N +1 i =0

Определив оценку корреляционной функции, можно вычислить и оценку спектральной плотности (11). С учетом четности корреляционной функции формулу (11) можно переписать в виде

∞

Sξ (ω) = 2∫ Kξ (τ) cosωτ dτ.

0

Учитывая, что оценка корреляционной функции (24) получена на интервале [0; T], получим следующую формулу для вычисления оценки спектральной плотности эргодического случайного процесса:

				N
ˆ	ˆ	(0)	+ 2	ˆ	(mΔτ) cos ωmΔτ,	(26)
Sξ	(ω) = Δτ Kξ			Δτ∑ Kξ
				m =1

где τ = T/N.

В данном цикле лабораторных работ предполагается, что рассматриваемые случайные процессы являются стационарными и эргодическими. Поэтому их статистические характеристики могут быть определены как по формулам (14) – (16)), т. е. путем усреднения по множеству реализаций, так и по формулам (19), (24), (25), предполагающим усреднение по времени, вычисляемое для одной реализации при достаточно большом времени наблюдения.

С учетом условия (18) время наблюдения Т выбирают из усло-

вия | ˆξ (τ) | < при > T, где — достаточно малое положительное

ε

τ

ε

K

9

число по сравнению с ˆξ (τ). Поскольку максимальное значение

K

ˆ	(τ) обычно достигается при τ = 0, то можно выбрать, например,
Kξ
	ˆ	(0)	=	ˆ
ε < 0,05 Kξ				0,05 Dξ .

1.2. Определение характеристик стационарного случайного процесса на выходе линейной системы

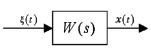
Рассмотрим линейную систему с постоянными параметрами, на вход которой поступает стационарный случайный процесс ξ(t). Система описывается своей передаточной функцией W(s) (рис. 1).

Рис. 1. Линейная система, на вход которой поступает случайный процесс

Ниже приведены формулы, позволяющие определить основные характеристики случайного процесса на выходе системы x(t), если известна ее передаточная функция и соответствующие характеристики входного случайного процесса ξ(t), в том числе математическое ожидание, спектральную плотность, автокорреляционную функцию и дисперсию случайного процесса x(t):

mx

= W(0)mξ ;

(27)

Sx (ω) =

W ( jω)

2 Sξ (ω);

(28)

1

∞

W ( jω)

2 Sξ (ω)e j ωt dω;

Kx

(t) =

∫

(29)

2π

−∞

1

∞

2

Dx =

∫

W ( jω)

Sξ (ω)dω.

(30)

2π

−∞

Приведенные формулы можно использовать и для формирования случайного процесса с заданными характеристиками из белого шума с помощью формирующего фильтра. Если случайный процесс ξ(t) на входе фильтра с передаточной функцией Wф(s) — белый шум, для которого mξ = 0, Sξ (ω) = с2, то в соответствии с при-

10