Билет 15. Авл-сбалансированные деревья

АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1. Это определение сбалансированности было дано Адельсоном-Вельским и Ландисом. Один из подвидов АВЛ-деревьев – деревья Фибоначчи, которые определяются так:

1. Пустое дерево есть дерево Фибоначчи высоты 0 (и, соответственно, высоты 1, если имеет 1 узел)

2. Если T_h-1 и T_h-2 – деревья Фибоначчи высот h-1 и h-2 соответственно, то - дерево Фибоначчи.

3. Других деревьев Фибоначчи нет.

Число узлов T_h определяется следующим рекуррентным соотношением:

N₀=0, N₁=1

N_h = N_h-1 + 1 + N_h-2, N_h – число узлов, для которых может реализоваться наихудший случай (верхний предел для h); такие числа называются числами Леонардо.

Теорема 1: Даже в наихудшем случае основные операции (поиск, вставка и удаление) с такими деревьями выполняются за O(log n).

Теорема 2: АВЛ-сбалансированное дерево никогда не будет выше идеально сбалансированного больше, чем на 45%.

Операция вставки:

Пусть новый узел вставляется в L, увеличивая его высоту на 1, тогда имеют место 3 случая:

1. h_l=h_r : после вставки высота становится неравной, но критерий балансировки не нарушается

2. hl < hr : высоты становятся равными, баланс только улучшается

3. hl > hr : критерий балансировки нарушается, и дерево требуется перестроить

Рассматриваем 2 случая (остальные варианты можно построить, исходя из соображений симметрии):

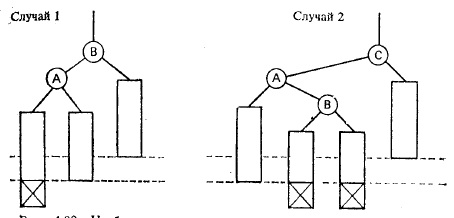
Одигарный поворот(LL) Двойной поворот(LR)

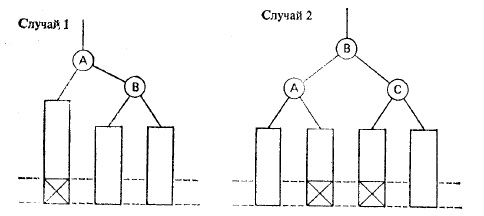
Также существует 2 зеркальных отображения RR и RL.

Алгоритм определения типа поворота (при добавлении в левое поддерево, с правым наоборот):

1. Находим ближайшую к низу вершину, которая является разбалансированной.

2. Рассмотрим ее левое поддерево. Если левое поддерево этого поддерева выше правого, то случай 1, иначе – случай 2.

3. Расставляем буквы и цифры, осуществляем поворот согласно схемам.

Сложность операции вставки: поворот влияет только на несколько ссылок и от размера дерева не зависит – О(1). Но требуется просмотр дерева сверху-вниз О(log n). Всего О(1)+2О(log n).

Операция удаления:

В среднем случае: на 2 включения 1 балансировка. А при удалении поворот в 1 случае из 5.

Процедура удаления из сбалансированного дерева строится на основе алгоритма удаления из обычного дерева. Простые случаи – концевые узлы и узлы с единственным потомком.

В худшем случае удаление проводится за O(log n).

Билет 16. Б-деревья

Б-дерево —дерево поиска. С точки зрения внешнего логического представления, сбалансированное, сильно ветвистое дерево во внешней памяти. Б-дерево предназначено для хранения информации на жёстком диске.

Сбалансированность означает, что длина любых двух путей от корня до листов различается не более, чем на единицу. Ветвистость дерева — это свойство каждого узла дерева ссылаться на большое число узлов-потомков.

Б-дерево порядка n обладает следующими свойствами:

• Каждая страница содержит не более 2n элементов.

• Каждая страница, кроме корневой, содержит не менее n элементов.

• Каждая страница представляет собой либо лист (не имеет потомков), либо имеет m+1 потомков, где m-число ключей на данной странице.

• Все страницы-листья находятся на одном уровне

Операции:

• Поиск ключа: Читаем страницу, ищем ключ, если не находим, то переходим по ссылке между 2 наиболее близкими к искомому ключами.

• Вставка: Если m<2n, то вставляем. Иначе создаем новую страницу, распределяем 2n ключей между ними, на 1 ключ (по значению средний) уходит наверх

• Удаление: Если m>n, то удаляем. Иначе берем элементы с соседней страницы (если не хватает, сливаем 2 страницы вместе).

Для дерева из N элементов для выполнения операций потребуется не более k=log_nN рекурсивных вызовов