
Решение задач на применение свойств делимости
Пример 1. Может ли натуральное число, имеющее 2000 делителей, быть полным квадратом?
Решение:
Число n
с каноническим разложением n=
является полным квадратом, если все
показатели
четны
=2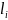 .
Количество делителей данного числа
можно найти по формуле
.
Количество делителей данного числа
можно найти по формуле
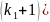 +1)…(
+1)…(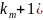 .
Так, число делителей числа 496=
.
Так, число делителей числа 496=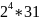 равно (4+1)(1+1)=10. Поскольку все скобки в
этом произведении нечетны, квадрат не
может иметь 2000 делителей.
равно (4+1)(1+1)=10. Поскольку все скобки в
этом произведении нечетны, квадрат не
может иметь 2000 делителей.
Ответ: такое число не может быть полным квадратом.
Определите, на какие натуральные числа может сокращаться дробь при целых х.
Решение: Пусть d – общий делитель числителя и знаменателя, тогда
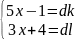
Для некоторых целых чисел K,l. Исключим x из этих уравнений:
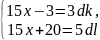 →d(51-3k)=23→d
– делитель 23, а т.к. 23 – простое число,
то d=23.
→d(51-3k)=23→d
– делитель 23, а т.к. 23 – простое число,
то d=23.
Ответ: на 23.
Пример 2. Найдите все натуральные числа, являющиеся степенью двойки, такие, что после зачеркивания первой цифры их десятичной записи снова получается десятичная запись числа, являющегося степенью двойки.
Решение: Из первых степеней двойки: 2,4,8,16,32,64,128,… числа 32 и 64 удовлетворяют условию задачи.
Зачеркнуть
цифру 3 числа 32, значит, из числа 32 вычесть
3*10, т.е. 32 – 3*10 = 2 , откуда получим 2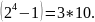
Зачеркнуть
цифру 6 числа 64, значит, из числа 64 вычесть
6*10, т.е. 64 - 6*10=4, откуда получим
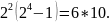
Таким образом, для искомой степени двойки должно выполняться равенство
 (1)
(1)
где k – количество цифр в десятичной записи искомой степени двойки после зачеркнутой цифры p.
В
правой части равенства (1) содержатся
множители 5, в левой части того же
равенства они могут содержаться только
в числе
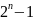 ( при условии n=4r,
r
– натуральное число ).
( при условии n=4r,
r
– натуральное число ).
Утверждение
«число
 ,
r
– натуральное число, делится на 5»
докажем методом математической индукции.
,
r
– натуральное число, делится на 5»
докажем методом математической индукции.
При
r
= 1число
 = 15 делится на 5.
= 15 делится на 5.
Предположим,
что при r=q
утверждение верно, т.е. число
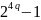 делится на 5, докажем, что тогда
делится на 5, докажем, что тогда
 делится
на 5. Число
делится
на 5. Число
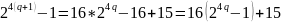
Делится на 5, так как делится на 5 по сделанному предположению, а 15 делится на 5.
Но тогда согласно принципу математической индукции число , r – натуральное число, делится на 5.
Из доказанного следует, что числа
 - не делятся на 5.
- не делятся на 5.
Из
доказанного следует, что числа
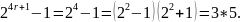 Именно для этого случая мы получили два
числа 32 и 64.
Именно для этого случая мы получили два
числа 32 и 64.
При
r
> 1 имеем
=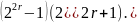
Ни
одного из чисел
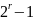 или
или
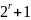 не
делится на 2. Если одно из них делится
на 5, то второе не делится на 5, так как
их разность 2 не делится на 5. Тогда это
второе число не делится ни на 2, ни на 5
и оно больше 15, т.е. больше числа p.
Поэтому равенство
не
делится на 2. Если одно из них делится
на 5, то второе не делится на 5, так как
их разность 2 не делится на 5. Тогда это
второе число не делится ни на 2, ни на 5
и оно больше 15, т.е. больше числа p.
Поэтому равенство

невозможно ни при каких условиях m и k.
Это означает, что условию задачи удовлетворяют лишь два числа 32 и 64.
Ответ:32,64.
Пример 3.Найдите все пары пятизначных чисел x, y, такие что число xy, полученное приписыванием десятичной записи числа y после десятичной записи числа x, делится на xy.
Решение:
По условию задачи число xy=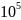 x+y
делится на xy,
т.е.верно равенство
x+y
делится на xy,
т.е.верно равенство
x+y=pxy, (1)
где p – натуральное число.
Перепишем равенство (1) в виде
x=(px-1)y.
Так как px-1 не делится на х, то у не делится на х, то есть у=qx, где q – натуральное число, меньшее 10 ( в противном случае у не пятизначное число).
Заменив в равенстве (1) у на qx и разделив полученное равенство на х, имеем:
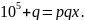
Так
как
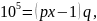 то
делится
на q.
Число
имеет делители, меньшие 10: 1, 2, 4, 5, 8.
Рассмотрим случаи q=1,
q=2, q=4, q=5, q=8.
то
делится
на q.
Число
имеет делители, меньшие 10: 1, 2, 4, 5, 8.
Рассмотрим случаи q=1,
q=2, q=4, q=5, q=8.
Если q=1, то равенство (3) имеет вид px=100001. Первыми делителями числа 100001 являются 1 и 11, но при p=1 и при p ≥ 11 число x не пятизначное.
Если q=2, то y=2x. Перепишем равенство (3) в виде px=50001. Первыми делителями числа 50001 являются числа 1,3 и 7.
При p=1 имеем: х=50001, у=100002, число у не пятизначное.
При р=3 имеем: х=16667, у=2*16667=33334.
При р ≥ 7 число х не пятизначное.
Итак, числа х=16667, y=33334 удовлетворяют условиям задачи.
Если q=4, то у=4х. Перепишем равенство (3) в виде рх=25001. Первыми делителями числа 25001 являются числа 1и 23.
При p=1 имеем: х=25001, у=100004, число у не пятизначное.
При p ≥ 23 число х не пятизначное.
Если q=5, то у=5х. И из равенства (3) следует, что рх=20001.
При р=1 имеем: х=25001, у=100005, число у не пятизначное.
При р > 1 число х не пятизначное.
Если q=8, то у=8х. Перепишем равенство (3) в виде рх=12501.
При р=1 имеем: х=12501, у=100008, число у не пятизначное.
При р > 8 число х не пятизначное.
Итак, в случаях 1), 3) – 5) не существует чисел х и у, удовлетворяющих условию задачи. Задача имеет единственное решение: х=16667, у=33334.
Ответ: х=16667, у=3334.
Пример 4. Среди обыкновенных дробей с положительными знаменателями, расположенными между числами 96/35 и 97/36 найдите такую, знаменатель которой минимален.
Решение. Сначала приведем дроби к общему знаменателю:
96/35=(96*35)/(35*36)=3456/1260;
97/36=(97*35)/(36*35)=3395/1260.
Теперь будем искать дробь с тем же знаменателем, числитель а которой – натуральное число от 3396 до 3455 – делится на наибольшее возможное произведение, составленной из делителей знаменателя.
Так как 2*1260 < 3396, а 6*630 > 3456, то сокращение искомой дроби не приводит к знаменателю 2.
Аналогично убеждаемся, что сокращение искомой дроби не приводит к знаменателям 3, 4, 5, 6. А так как 1260=7*180 и 3396 < 180*19 < 3456, то искомую дробь 180*19/1260 можно сократить на 180, при этом получится наименьший возможный положительный знаменатель 7.
Второй способ решения. Найдем искомую дробь так:
97/36=2 25/36<2 25/35=2 5/7; 96/35=2 26/35. Так как 2 25/35 < 2 26/35, то 97/36 < 19/7 < 96/35.
Так как 2 < 2 25/36 < 2 26/35 < 3, то дроби со знаменателям 1 (то есть натурального числа) в указанном промежутке нет. Так как
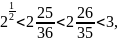
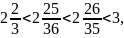

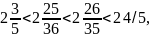
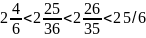 ,
,
То дроби со знаменателями, меньшими 7 в указанном промежутке нет.
Ответ: 19/7.
Пример 5. Произведение нескольких различных простых чисел делится на каждое их этих чисел, уменьшенное на 1. Чему может быть равно это произведение?
Решение. Искомое произведение – четное, поскольку оно делится на каждый простой сомножитель, уменьшенный на 1. Следовательно, один из простых сомножителей – число 2.
Последующие сомножители получим, увеличивая на 1первый сомножитель, а затем – произведение сомножителей, найденных ранее:
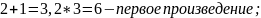
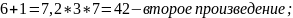
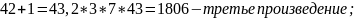
1806+1=1807.
Поскольку число 1807 составное (1807=139*13), то цепочка сомножителей завершается числом 43.
Итак, произведение, отвечающее условию, может быть равно 6, 42 или 1806.
Ответ: 6, 42, 1806.
Пример 6. Найдутся ли хотя бы три десятизначных числа, делящиеся на 11, в записи каждого из которых использованы все цифры от 0 до 9?
Решение. Число делится на 11 тогда и только тогда, когда разность между суммами его цифр, стоящих на нечетных и на четных местах, делятся на11.
Запишем все цифры подряд: 9876543210. В написанном числе указанная разность сумм равна 5. Меняя местами, например, 5 и 8, мы одну сумму увеличиваем на 3, а другую уменьшаем на 3. Значит, разность между суммами его цифр, стоящих на нечетных и на четных местах, становится равной 11. Меняя местами, например,4 и 7, или 3 и 6, получаем требуемые примеры. Примечание. В задаче не требуется нахождение всех чисел, обладающих указанным свойством. Ответ: Да.
Пример
7. Докажите,
что число
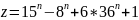 делится
на 14 при любом числе n.
делится
на 14 при любом числе n.
Решение:
По формуле
 …+
…+
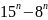 =
=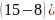 …+
…+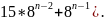
Третье
слагаемое запишем как степень шести:
6*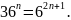 Применим
к третьему и четвертому слагаемым
формулу
…-
Применим
к третьему и четвертому слагаемым
формулу
…-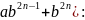
 …-
…-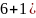 .
.
Так
как
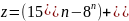 )
и оба слагаемых делятся на 7, по первому
свойству, число z
делится на 7. Кроме того, z
четно, поскольку четными являются числа
)
и оба слагаемых делятся на 7, по первому
свойству, число z
делится на 7. Кроме того, z
четно, поскольку четными являются числа
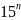 +1,
+1,
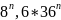 .
.
Итак, число z делится на 14.
Пример
8. При каких
натуральных значениях n
число
 является простым?
является простым?
Решение:
Чтобы разложить данное выражение на
множители, можно разбить 3 на 2 и 1 и затем
сгруппировать слагаемые (это не
единственный способ, вместо этого можно
найти корни данного трехчлена по формуле
или выделить полный квадрат):
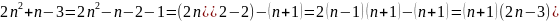 .
Для того, чтобы это выражение имело
простое значение, нужно, чтобы одна
скобка равнялась 1, в это время как вторая
была простым членом.
.
Для того, чтобы это выражение имело
простое значение, нужно, чтобы одна
скобка равнялась 1, в это время как вторая
была простым членом.
Если n+1=1, то n=0, но 0 не является натуральным числом. Если 2n-3=1, 2n=3+1, 2n=4, n=2. При этом n+1=3 – простое число.
Ответ: n =2.
Пример
9. Может ли
число
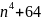 быть
простым при каких-либо целых n?
быть
простым при каких-либо целых n?
Решение:
Дополним
выражение
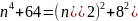 до
квадрата суммы:
до
квадрата суммы:
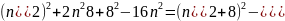 Для простоты
необходимо, чтобы один из сомножителей
равнялся 1,а второй был простым членом,
однако уравнения
Для простоты
необходимо, чтобы один из сомножителей
равнялся 1,а второй был простым членом,
однако уравнения
 не
имеют решений.
не
имеют решений.
Ответ: число составное при любом целом значении n.
Пример 10. Доказать, что число делится на 14 при любом натуральном значение числа n.
Решение:
=
…+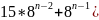 делится
на 7.
делится
на 7.
Третье слагаемое запишем как степень шести: 6*
…- .
Так
как
)
и обе скобки делятся на 7, то z
делится на 7. Кроме того, числа
+1,
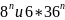 четные, поэтому z
делится на 2.
четные, поэтому z
делится на 2.
Пример 11. Разложите на множители число 42780.
Решение: Очевидно, что данное число делится на 3, 4= и 5. Следовательно, 42780= *3*5*713. Для отыскивания делителей 713 применим метод Ферма:
713+1=714,
713+1+3=717, 713+1+3+5=722, 713+1+3+5+7=729=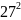 .
.
Отсюда
713=
- =(27-4)(27+4)=23*31.
=(27-4)(27+4)=23*31.
Ответ: 42780= 42780= *3*5*23*31.
Пример 12. Найдите все делители числа 496 и сумму его собственных делителей.
Решение:
496=8*62=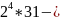 каноническое
разложение этого числа на простые
множители. Находим делители: 1,2,
=4,
=8,
каноническое
разложение этого числа на простые
множители. Находим делители: 1,2,
=4,
=8,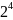 =16
и 31, 2*31=62,4*31=124,8*31=248 и само число 496. Теперь
сложим найденные числа:
1+2+4+8+16+31+2*31+4*31+8*31= (для удобства подсчета
сгруппируем слагаемые)
=(1+31)+(2+2*31)+(4+4*31)+(8+8*31)=32*(1+2+4+8)+16=16*(1+2+4+8+16)=16*31=496.
=16
и 31, 2*31=62,4*31=124,8*31=248 и само число 496. Теперь
сложим найденные числа:
1+2+4+8+16+31+2*31+4*31+8*31= (для удобства подсчета
сгруппируем слагаемые)
=(1+31)+(2+2*31)+(4+4*31)+(8+8*31)=32*(1+2+4+8)+16=16*(1+2+4+8+16)=16*31=496.
