По определению

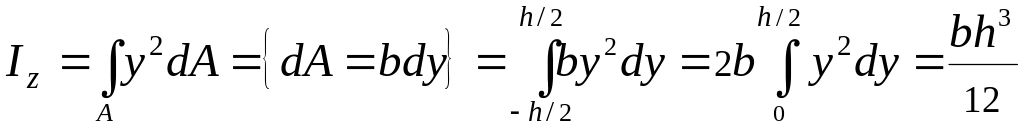
Для прямоугольника ; .

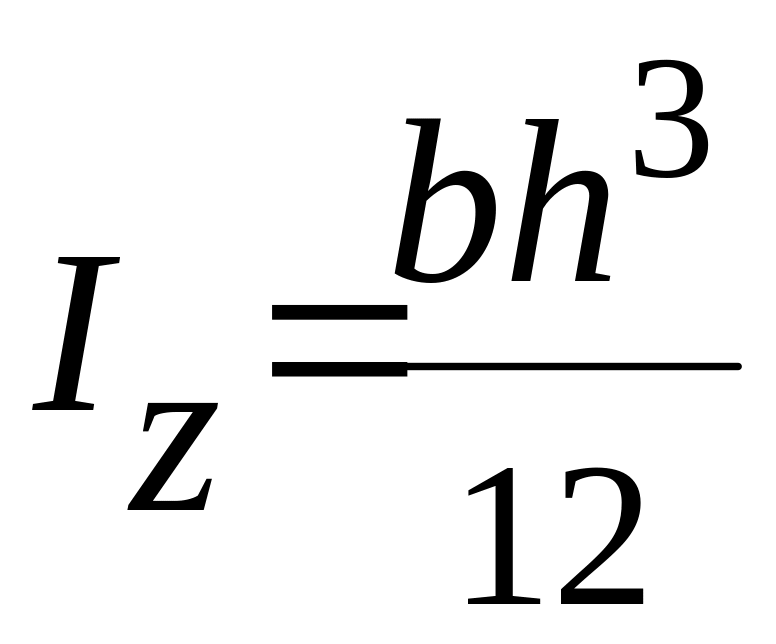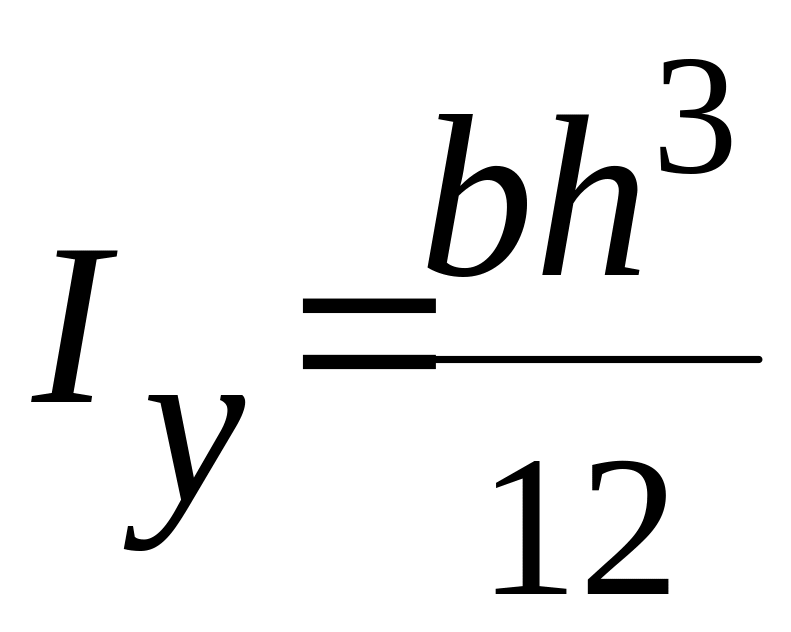Пример 2: Определить момент инерции треугольника относительно оси, проходящей через его основание (рис. 14).

Выделим элементарную площадку, параллельную указанной оси,

,

где b(y) - ширина треугольника на расстоянии y от оси Oz.

Рассматривая подобные треугольники, имеем такие соотношения между их сторонами:

; .

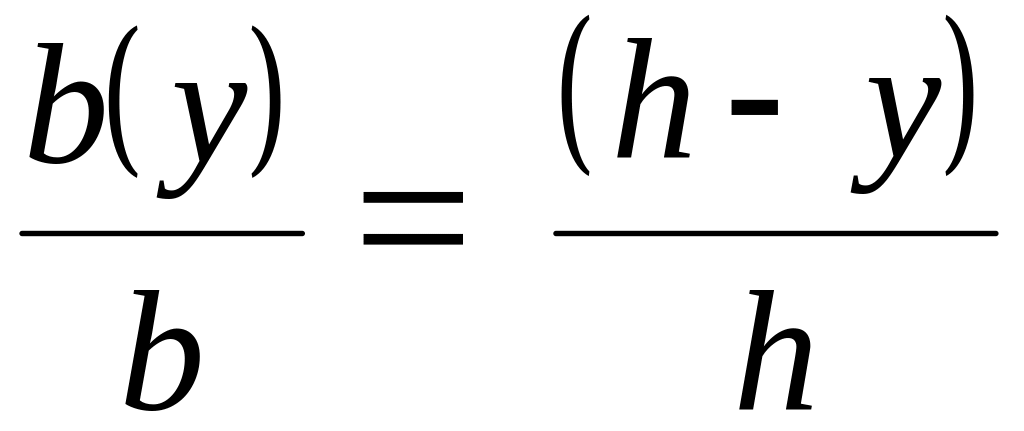Момент инерции по определению

;

Для треугольника .

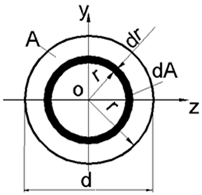
Пример 3: Определить момент инерции круга относительно его центра и центральных осей (рис. 18).

Выделим элементарную площадку в виде бесконечно тонкого кольца с радиусом  и толщиной d. Площадь такого элемента

Полярный момент инерции по определению

Рис. 18

Известно, что . Относительно круга в результате симметрии

Следовательно для круга

При определении моментов инерции сложных сечений (рис. 15) последние можно разбить на простые части, моменты инерции которых известны. Момент инерции сложной фигуры равняется сумме моментов инерции ее составляющих частей, то есть

.

Если в сечении есть отверстие, его считают частью фигуры с отрицательной площадью.

3.3. Моменты инерции относительно параллельных осей

Пусть известны моменты инерции относительно центральных осей z₁ , y₁, а именно

Н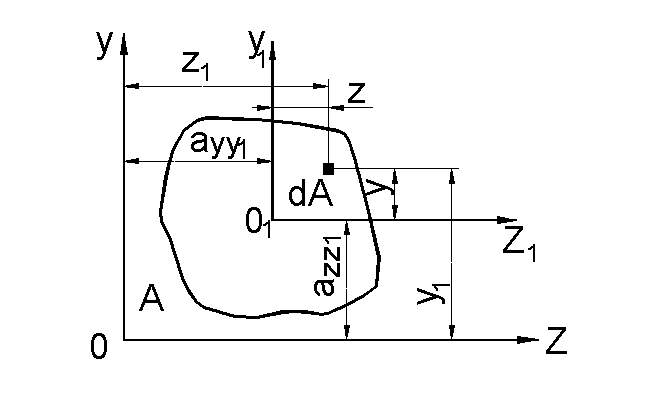 еобходимо определить моменты инерции относительно осей z , y, которые параллельны центральным (рис. 19).

К

Рис. 19

оординаты любой точки в новой системе zOy можно выразить через координаты в центральных осях z₁Oy₁ ; ,

где  расстояния между осями z, z₁, y и y₁, соответственно, или координаты начала координат z₁Oy₁ точки O₁ , в системе координат z O y .

Подчеркнем, что координаты во всех формулах нужно подставлять, учитывая их знаки.

Момент инерции I_z по определению

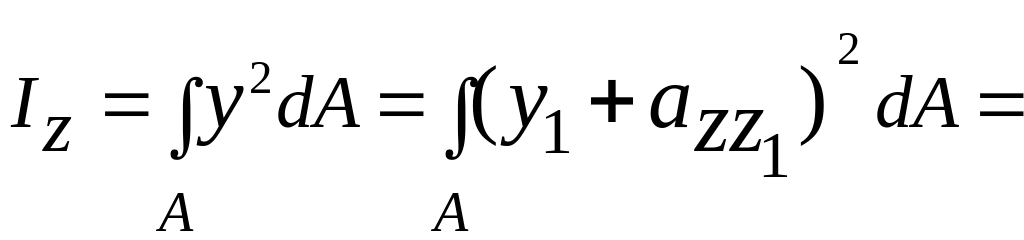
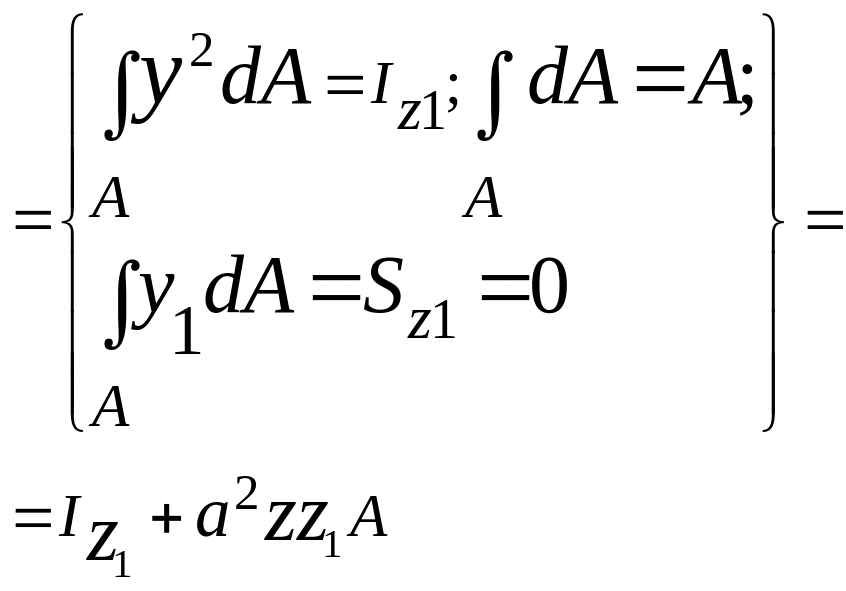
Статический момент равняется нулю, поскольку он вычисляется относительно центральной оси Oz₁ .

Следовательно, .

Аналогично ,

.

Момент инерции фигуры относительно произвольной оси равняется моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между этими осями.

Ц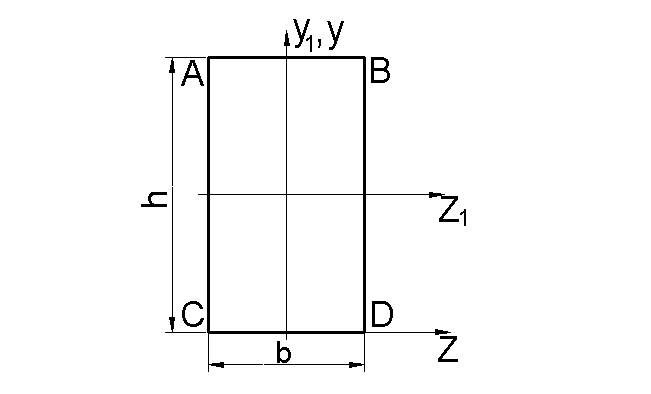 ентробежный момент инерции относительно произвольной системы взаимно перпендикулярных осей равняется центробежному моменту инерции относительно центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.

Пример. Определить момент инерции прямоугольника относительно оси Oz, которая проходит через его сторону CD (рис. 20).

.

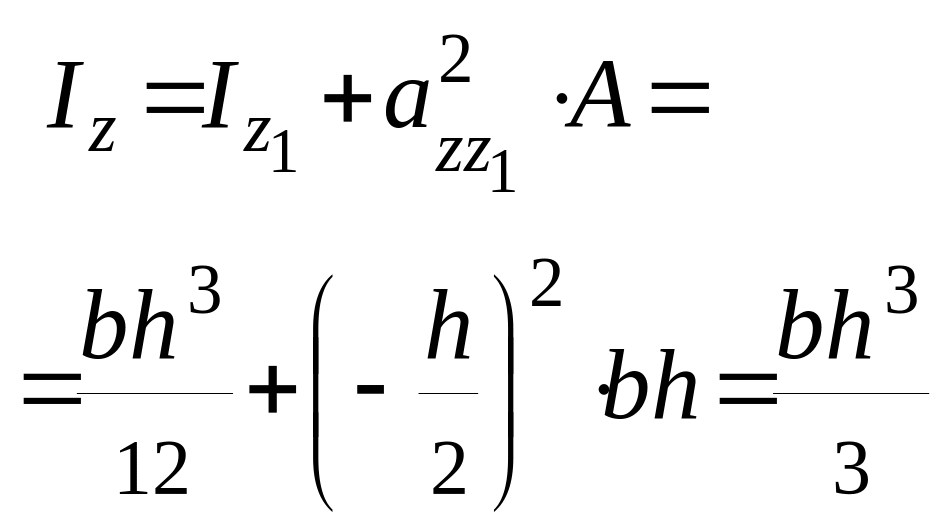Из примера видим, что момент инерции сечения относительно центральной оси, всегда будет меньше, чем момент инерции относительно параллельных осей.

3.4. Зависимость между моментами инерции в случае поворота координатных осей

Пусть известны моменты инерции фигуры (рис. 21) относительно координатных осей z₁ O y₁, например:

; ; .

П овернем оси Oz₁, Oy₁ на угол  против часовой стрелки, принимая угол поворота осей в этом направлении положительным.

Координаты произвольной элементарной площадки в новых осях zOy можно выразить через ее координаты z_1., y₁ в исходной А системе по таким формулам:

Рис. 21

;

.

Найдем теперь моменты инерции сечения А относительно осей zOy :

;

;

.

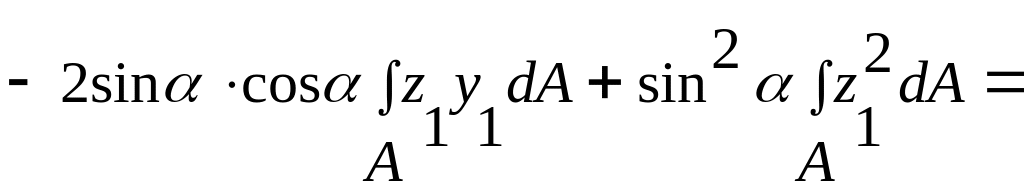
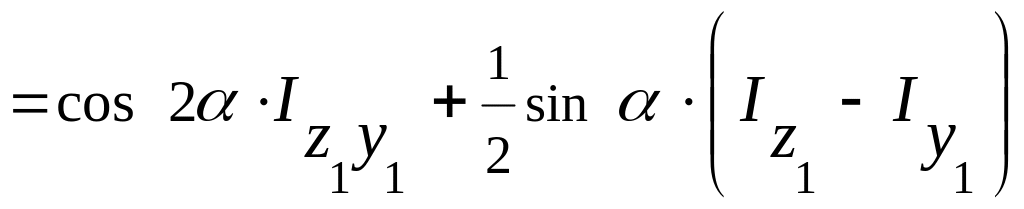Отсюда, зависимость между моментами инерции в случае поворота координатных осей имеет примет вид

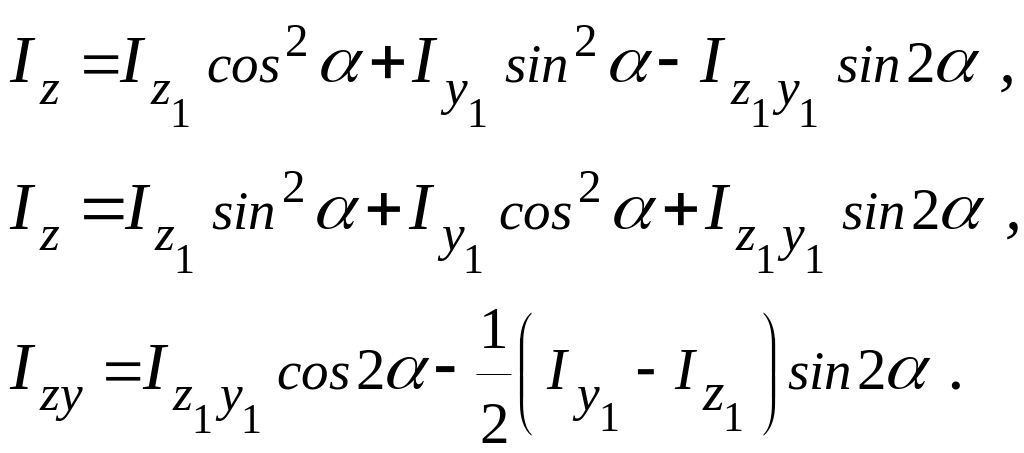
Если просуммировать почленно выражения для вычисления I_z и I_y , то получим еще одну зависимость, а именно:

В случае поворота прямоугольных осей сумма осевых моментов инерции не изменяется и равняется полярному моменту инерции относительно начала координат.

При условии поворота системы осей на угол  = 90

, , .