Ульяновский государственный университет Инженерно-физический факультет высоких технологий Кафедра инженерной физики	Форма
Титульный лист

ОТЧЕТ К ЛАБОРАТОРНОЙ РАБОТЕ

Название работы:

СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ В МОЛЕКУЛЯРНОЙ ФИЗИКЕ

Факультет ИФФВТ	Работа № 6
Группа СтС-11	Дата выполнения 6.12.10
ФИО преподавателя Богданова Д.А.	ФИО студента Феткуллова А.Р.

Подпись исполнителя

Работу принял “_____” ____________ 2010 г.

Подпись и ФИО преподавателя

Цель работы: Ознакомление с основными статистическими закономерностями идеальных газов.

Приборы и принадлежности: персональный компьютер, программа LabStat.exe

Краткая теория:

В молекулярной физике изучается поведение систем, состоящих из большого числа частиц. Обычно в 1см³ твердого тела содержится 10²² -10²³ атомов. Уравнения классической механики не могут быть использованы для описания таких систем, т.к. это требует решения системы дифференциальных уравнений , количество уравнений при этом совпадает с числом частиц в системе. Очевидно, что такая система уравнений не может быть решена для реальных систем, поэтому чаще всего для описания используется вероятностный подход, изучаемый статистической физикой.

В ероятность

В соответствии вероятностным подходом некоторые физические величины, характеризующие конкретные частицы (такие как координаты, импульс, энергию), имеют случайные значения. Такие величины в теории вероятностей называют случайными.

Случайная величина – величина, значение которой нельзя предсказать заранее.

Для описания случайных величин вводится понятие вероятности, которое мы обсудим на примере молекулы, находящейся в объеме V (рис.1). Пусть частица случайным образом блуждает в объеме V, и выйти за пределы этой области не может. Предположим, что мы проводим N_ex экспериментов, результатом, которых является проверка наличия одной частицы в объеме V₁. Если из всех N_ex экспериментов N₁, соответствует такому событию, тогда по определению вероятностью называется величина P(V₁):

(1)

Если случайная величина может принимать дискретный набор значений, то ее характеризуют набором вероятностей всех возможных событий , называемым распределением вероятностей.

Обсудим одно из важнейших свойств распределения вероятностей, на примере блуждающей частицы в объеме V. Если в пределах объема V выделить несколько непересекающихся элементов объема V_i, тогда можно ввести вероятности попадания в каждый из них P_i по аналогии с (1)

(1a)

Если , тогда очевидно, что , а для вероятностей выполняется условие нормировки:

(2)

Характер распределения вероятностей обычно зависит от свойств самой системы. Эту связь можно продемонстрировать на примере блуждания частицы в объеме V, разделенном на элементы объема V_i. Если предположить, что все возможные расположения частиц в системе являются равноправными, то вероятности p_i должны быть пропорциональны соответствующему объему , где A – константа, определяемая из условия нормировки (2):

,

Из этого следует, что вероятность

. (3)

Во многих случаях приходится работать со случайными величинами, которые могут принимать непрерывные значения (например, координаты частиц). В этом случае распределение вероятностей записывается с помощью функции называемой плотностью вероятности f(x), которая устанавливает связь между вероятностью и интервалом изменения случайной величины. Вероятность такого события, что случайная величина x лежит в пределах (x₀, x₀+dx) определяется формулой:

(4)

Вероятность того, что случайная величина x лежит в пределах от x₁ до x₂ определяется интегралом:

, (5)

Условие нормировки (2) для случая непрерывного изменения случайной величины x переписывается в виде

, (6)

где интегрирование ведется по всей области определения случайной величины .

Независимые события

Определим вероятность события, когда в одном из измерений частица попадает в объем , а при другом измерении частица попадает в другой объем . Вероятность такого события определяется теоремой об умножении вероятностей:

(7)

В случае непрерывных случайных величин x и y плотность вероятности определяется произведением функций плотности вероятности для каждой из случайных величин ( ):

(8)

Биноминальное распределение

Рассмотрим систему объемом V, в которой находится N частиц. Определим вероятность события, в соответствии с которым ровно m частиц попадают в объем V₁.

Вероятность того, что m частиц попали в объем V₁, в соответствии с (3) и (7):

(9)

При этом остальные частиц должны попасть в объем . Вероятность этого события:

(10)

Следует учесть, что все частицы в системе одинаковы и обладают идентичными свойствами (неразличимы). Это означает, что m частиц могут быть выбраны из полного числа N произвольным образом. Количество способов выбрать m частиц из полного набора N задается формулой:

(11)

Таким образом, пользуясь теоремой об умножении вероятностей (7) и соотношениями (9-11) получим выражение для вероятности :

(12)

Выражение (12) называется биноминальным распределением. С помощью бинома Ньютона для распределения (12) может быть легко проверено выполнение условия нормировки (2)

(13)

где использовано определение .

Вычисление средних значений физических величин

Для характеристики случайной величины часто пользуются понятием среднего значения, которое определяется как:

(14)

Мерой отличия случайной величины x от среднего значения является дисперсия (среднеквадратичное отклонение), которая определяется как:

(15)

Раскрывая скобки и пользуясь определением средних величин можно получить простое выражение для расчета дисперсии:

(16)

В качестве примера рассчитаем средние значения и дисперсию для биноминального распределения. Установим среднее значение числа частиц попадающих в область V₁ - . По определению среднее значение

.

Для расчета дисперсии биноминального распределения воспользуемся формулой (15) и результатом вычисления . Расчет можно провести аналогично :

Подстановка этой формулы в (15) приводит к значению дисперсии в биноминальном распределении:

Вычисление средних значений физических величин, зависящих от случайной величины x, проводится аналогично (14). Если известны вероятности различных состояний системы p_i, при этом требуется вычислить значения какой-либо физической величины u имеющей разные значения в каждом из состояний u_i=u(x_i). Вычисление среднего значения производится в соответствии с формулой:

(17)

В случае непрерывного распределения вероятности выражение для среднего значения величины u(x) определяется через функцию плотности вероятности f(x):

(15)

Распределение Гаусса

Распределение Гаусса достаточно часто встречается при описании реальных физических систем. Одной из основных задач, приводящих к получению распределения Гаусса, является задача о случайном блуждании частицы на плоскости. Если частица начинает блуждания из начала координат, то вероятность ее обнаружения через некоторое время в области площадью dxdy в окрестности точки (x₀, y₀), определяется в виде:

где функция f(x) - распределение Гаусса для случайной величины x:

(16)

Здесь - среднее значение случайной величины x, - среднеквадратичное отклонение случайной величины x. График функции f(x) приведен на рис.2

Распределение Максвелла

Распределение Максвелла определяет функцию распределения частиц идеального газа по скоростям. По своему виду распределение Максвелла совпадает с распределением Гаусса, когда в качестве случайных величин выбираются проекции скорости молекул. Функция плотности вероятности для проекции скорости :

(17)

Поскольку компоненты скорости являются независимыми, то выражение (17) может быть перенесено и на компоненты скорости и . Общий вид графика функции (17) соответствует зависимости представленной на рис. 2.

В соответствии с (17) может быть получено распределение по модулю скорости:

(18)

График функции F(v) зависит от температуры

Распределение Максвелла F(v) может быть охарактеризовано несколькими характерными значениями скорости:

,

г де - среднее значение модуля скорости, - наиболее вероятное значение скорости, - среднеквадратичное значение модуля скорости.

Вычисление среднего значения кинетической энергии молекул идеального газа, описываемых распределением Максвелла, может быть получено в виде:

(19)

Экспериментальные данные, их обработка и расчет погрешности:

Упражнение 1:

Номер грани	1	2	3	4	5	6
Количество событий	176	169	163	163	172	157
Вероятность, отн.ед.	0,176	0,169	0,163	0,163	0,172	0,157

0,176+0,169+0,163+0,163+0,172+0,157=1

Вывод: условие нормировки выполняется.

Упражнение 2:

№	N1	N2	N3
1.	33	157	810
2.	37	157	806
3.	48	165	787
4.	42	169	789
5.	50	161	789
6.	33	157	810
7.	46	152	802
8.	50	169	781
9.	34	159	807
10.	37	178	785
	41	162,4	796,6
	0,041	0,1624	0,7966
	0,0021	0,0042	0,0042
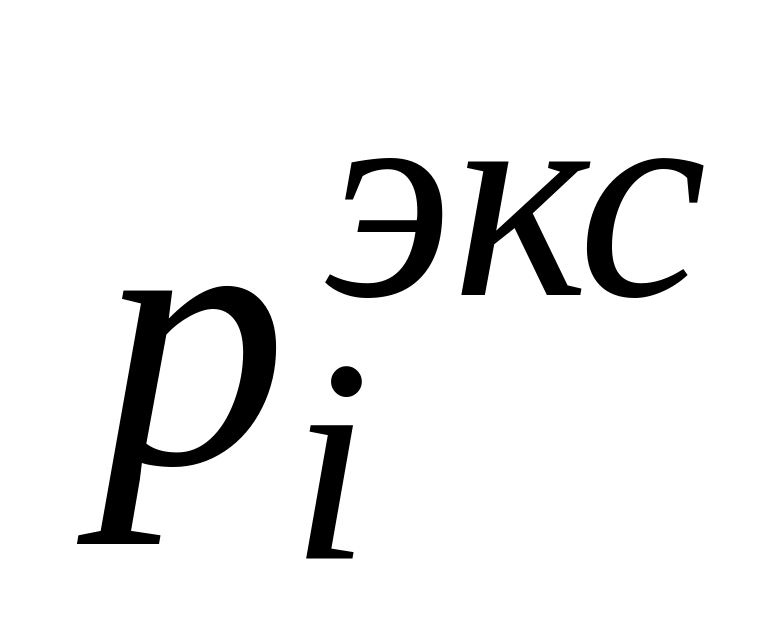
	0,041±0,005	0,1624±0,0097	0,7966±0,0097
	0,04	0,16	0,8

= , где

0,7966+0,1624+0,041=1

Вывод: с учетом погрешности , что доказывает выполнение условия нормировки.