Оптимальное и эффективное кодирование

1. Понятие кодирования. Кодовое дерево.

В процессе кодирования каждая буква исходного алфавита представляется различными последовательностями, состоящими из кодовых букв или цифр.

Если исходный алфавит содержит m букв, то для построения равномерного кода с использованием D кодовых букв необходимо обеспечить выполнение следующего условия:

,

где n- количество элементов кодовой последовательности.

Для построения равномерного кода достаточно пронумеровать буквы исходного алфавита и записать их в коды как n-разрядное число в D-ичной системе счисления.

Заметим, что поиск равномерного кода означает, что каждая буква исходного алфавита m кодируется кодовой последовательностью длинной n. Очевидно, что при различной вероятности появления букв исходного алфавита равномерный код является избыточным, так как энтропия, характеризующая информационную емкость сообщения максимальна при равновероятных буквах исходного текста:

.

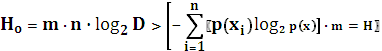При этом - энтропия кода одной буквы в n - разрядном D- ичном числе. Таким образом, информационные возможности кода используются не полностью.

Пример. Для двоичного 5-рарядного кода букв русского алфавита информационная емкость составляет 5 бит, =4,35 бит.

Устранение избыточности достигается применением неравномерных кодов, в которых буквы, имеющие наибольшие вероятности, кодируются короткими кодовыми последовательностями, а более длинные комбинации присваиваются редким, имеющим меньшую вероятность буквам.

Если i-ая буква, вероятность которой p_i, получает кодовую комбинацию длины n_i, то средняя длинна кода или средняя длина кодового слова равна:

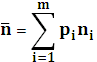
Введем понятие кодового дерева, которым часто пользуются при рассмотрении Известно, что любую букву или событие, содержащиеся в алфавите источника или в сообщении, можно разложить на последовательности двоичных решений с исходами «ДА»=1 и «НЕТ»=0, причем без потери информации. Таким образом, каждой букве исходного алфавита может быть поставлена в соответствие или, как говорят, приписана некоторая последовательность двоичных символов - 0 или 1.А такую последовательность называют кодовым деревом. При этом потери информации не происходит, так как каждое событие может быть восстановлено по соответствующему кодовому слову.

Уровень

КД

Число узлов

Корень

0

1

0

1

1

2

0

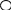
2

4

3

8

4

16

1

1

0

С₁

1

0

1

0

10

0

С₂

С₃

1

0

1

0

1

0

1

0

С₁₁

С₁₀

С₉

С₈

С₇

С₆

С₅

С₄

C₁,C₂,…,C₁₁-кодовые слова. Уровень кодового дерева определяет длину кодового слова.

2. Теорема кодирования источников, неравенство Крафта.

Префиксный код.

Теорема Шеннона о кодировании источников устанавливает связь между средней длинной кодового слова и энтропией источника.

Для любого дискретного источника без памяти X с конечным алфавитом и энтропией H(X) существует D- ичный префиксный код, в котором средняя длинна кодового слова , удовлетворяет неравенству:

В префиксном коде никакое кодовое дерево не является префиксом другого кодового дерева. Это значит, что поток кодовых слов может использоваться без специального разделения этих слов. Например, если код 101 является кодом какой-то буквы, то в качестве кодов других букв нельзя использовать следующие комбинации: 1,10,10101, …и т.д.

Из теоремы Шеннона следует, что тем ближе длина кодового слова к энтропии источника, тем более эффективно кодирование. В идеальном случае, когда , код называют эффективным. Эффективность кода оценивается величиной:

.

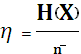Если средняя длина кодового слова является минимально возможной, то код еще и оптимальный. Теорема кодирования источников доказывается с использованием неравенства Крафта и формулируется следующим образом.

Для существования однозначно декодируемого D- ичного кода, содержащего k кодовых слов с длинами n₁,n₂,…,n_k, необходимо и достаточно, чтобы выполнялось неравенство Крафта: