
- •Непрерывность и дифференцируемость комплексных переменных
- •П1.1 Предел последовательности комплексных чисел.
- •Свойства аналитической функции:
- •Тема 2: Интегрируемые теоремы. Интегральная форма
- •Свойства интегралов:
- •Тема: Оценка интеграла.
- •Свойства непрерывных функций:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •П(7.1) Локальные свойства отображения регулярных функций
- •Теорема Лема Шварца
- •П. (7.2) Общие свойства конформных отображений
- •Преобразование Лапласа.
- •Свойства преобразований Лапласа:
- •9) Изображение свёртки.
- •Метрические и топологические пространства.
- •Мера, интеграл Лебега
Свойства аналитической функции:
1.Если функция F(z) является аналитической в области Д, то она непрерывна в этой области.
2.Если
f1(z) и f2(z)
являются аналитическими в области Д,
то их сумма является также аналитической
функцией в области Д, а функция ϕ(z)= является аналитической везде, где
f2(z)≠0.
является аналитической везде, где
f2(z)≠0.
3. Если w=f(z) является аналитической функцией в области Д, причём в области её значений на плоскости w определяется аналитической функцией s=ϕ(w), то функция F(z)=ϕ[f(z)] является аналитической функцией комплексной переменной.
4.Если
w=f(z)
является аналитической функцией в
области Д, причём |f’(z)|≠0
в окрестности некоторой точки
ϵД,
то в окрестности точки
 область значений f(z)
определяет обратная функция z=ϕ(w).
Является аналитической функцией
комплексной переменной w.
При этом имеет место соотношение: f’(
область значений f(z)
определяет обратная функция z=ϕ(w).
Является аналитической функцией
комплексной переменной w.
При этом имеет место соотношение: f’(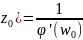
Рассмотрим геометрический смысл производной функции W. W=f(z)
Пусть ɣ1
 ; ɣ2
; ɣ2 ,
если ϕ – угол между ɣ1 и ɣ2
в точке
,
если ϕ – угол между ɣ1 и ɣ2
в точке
 ,
то ϕ – также угол между
,
то ϕ – также угол между
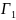 и
и
 в точке W0. Сохраняя
не только абсолютную величину угла, но
и его направление.
в точке W0. Сохраняя
не только абсолютную величину угла, но
и его направление.
Определение: Отображаемой окрестностью в точке на окрестность точки W0 осуществляется аналитической функцией W=f(z) и обладает в точке свойством сохранения углов и постоянством растяжений называется комфортным отображением.
Так как определение производной комплексной функции аналогично определению производной функции действительной переменной то сохраняя формулы дифференцирования получим
(az+b)’=a
(z2)=2z (1.8)
( )=
-
)=
-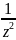
Так же производную можно вычислить по следующим формулам:
f’(z)=ux(x,y)+ivx(x,y)=vy(x,y)+ivx(x,y)=ux(x,y)-iuy(x,y)=vy(x,y)-iuy(x,y) (1.9)
Тема 2: Интегрируемые теоремы. Интегральная форма
П2.1 Интеграл функций комплексной переменной
Пусть на кривой g определяется комплекснозначная функция f(z). Разобьём её на дуги ɣ1, ɣ2,…,ɣn точками z1, z2, …, zn и т. д. временными по направлению движения кривой ɣ – начало кривой, zn – ее конец. На каждой дуге ɣk выберем точку ξk из ɣk и составим интегральную сумму:
 (2.1)
(2.1)
l=max
1≤k≤n,
где
-длинна
дуги
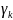 ,
если существует предел при
,
если существует предел при
 ,
выражение (2.1), то он называется интегралом
от функции f(z)
по кривой ɣ т.е.
,
выражение (2.1), то он называется интегралом
от функции f(z)
по кривой ɣ т.е. (2.2)
(2.2)
Пусть z=x+iy,
f(z)=u(x;y)+iv(x;y),
тогда интеграл (2.2) можно записать в
виде:
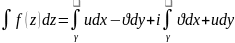 (2.3)
(2.3)
Значит существует
интеграл
 равносильно существованию 2-х криволинейный
интеграл от действительных функций
равносильно существованию 2-х криволинейный
интеграл от действительных функций
 и
и
 ,если кривая ɣ задаётся уравнением
z=δ(t)=ξ(t)+iη(t)
tϵ[α,β],
то в формуле (2.3)
,если кривая ɣ задаётся уравнением
z=δ(t)=ξ(t)+iη(t)
tϵ[α,β],
то в формуле (2.3)
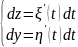
Из этого следует, что:
= (2.4)
(2.4)
Интеграл
 зависит только от начала и конца кривой
ɣ и не зависит от пути интегрирования,
поэтому
зависит только от начала и конца кривой
ɣ и не зависит от пути интегрирования,
поэтому
 т.е интеграл
т.е интеграл
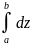 по любой замкнутой кривой равен нулю.
по любой замкнутой кривой равен нулю.
Свойства интегралов:
Непрерывная на кривой функция- интегрируема на этой кривой. Следующие свойства вытекают из криволинейного интеграла.
1) (2.5)
(2.5)
2) (2.6)
(2.6)
При изменении ориентации кривой интеграл меняет знак.
3) (2.7)
(2.7)
