1. Графы: ориентированные и неориентированные. Определение, способы задания, примеры. Утверждение о количестве ребер графа с n вершинами.

Совокупность множества M с заданным на нем бинарным отношением T принадлежит M² называется графом G = < M,T >, где M – носитель графа – множество вершин, изображаемых точками; Т – сигнатура графа – множество линий, обозначающих отношения и называемых ребрами.

Граф называется ориентированным(орграфом), если он содержит направленные ребра(дуги). Соответственно граф с неориентированными ребрами называется неориентированным.

Граф можно задать следующими способами:

1. Матрицей смежности, где каждой i-й строке(j-му столбцу) однозначно сопоставляют элемент множества M, между которыми выполняется отношение смежности. Т.е. 2-е вершины, инцендентные одному ребру, смежны. Два ребра, нцендентные одной вершине, тоже смежны. Тогда каждая клетка b_ij взаимно однозначно соответствует элементам множества M*M = M². Клетку b_ij, которая соответствует элементу, принадлежащему бинарному отношению T принадлежащему М², отмечают, например, единицей, а в остальные клетки, записывают нули.

2. Перечислением дуг, например:

M = {a,b,c,d,e}, T={(a,b),(a,c),(a,d)…(e,c)}

3) Фактор-множества, представленного парами «элемент множества М – подмножество М, представляющее собой окрестность единичного радиуса этого элемента» [<a,{b,c,d,}>…<e,{c}>]

4) Орграф может быть задан матрицей инциндентности А размерностью n*m: А = ||a_ij||, где n= |M|, m=|T|, у которой a_ij = 1, если a_i является концом пути t_j, -1 если a_i является началом пути t_j, 0 если вершина a_i не инцендентна дуге t_j.

Количество ребер в полном графе с N вершинами равно N(N − 1)/2.

2. Степени вершин неориентированного графа. Источник и сток. Степени входа и выхода ориентированного графа. Примеры.

Степень вершины — количество рёбер графа G, инцидентных вершине x. Обозначается d(x). Минимальная степень вершины графа G обозначается δ(G), а максимальная — Δ(G).

Изолированной вершиной называется вершина, у которой и степень входа, и степень выхода равны  .

 Источником называется вершина, степень выхода которой положительна, а степень входа равна  . 

Стоком называется вершина, степень входа которой положительна, а степень выхода равна  .

Степенью выхода вершины   ориентированного графа называется число выходящих из   дуг (ребер). Степенью входа вершины  ориентированного графа называется число входящих в   дуг (ребер).

3. Основные утверждения о степенях вершин графов.

Степенью вершины в графе называется число выходящих из нее ребер. В ориентированном графе у каждой вершины есть 2 степени: входящая (число ребер, входящих в вершину) и исходящая (число ребер, выходящих из вершины). Мы говорим, что вершина графа четная, если ее степень четна, и что вершина нечетная - в противном случае (в графе на рис. наверху все вершины четные). Для ориентированного графа понятие четности вершины обычно не вводится. В графе степени вершин и количество ребер связаны важными соотношениями:

4. Изоморфизм графов. Построение изоморфизма. Примеры.

Определение. На множестве неориентированных графов введем бинарное отношение, называемое отношением изоморфизма, которое определим следующим образом: будем говорить, что графы и связаны отношением изоморфизма,, если существует пара взаимно однозначных отображений и таких, что для любого ребра выполнено условие:

.

Графы и , связанные отношением изоморфизма, называют изоморфными и пишут .

П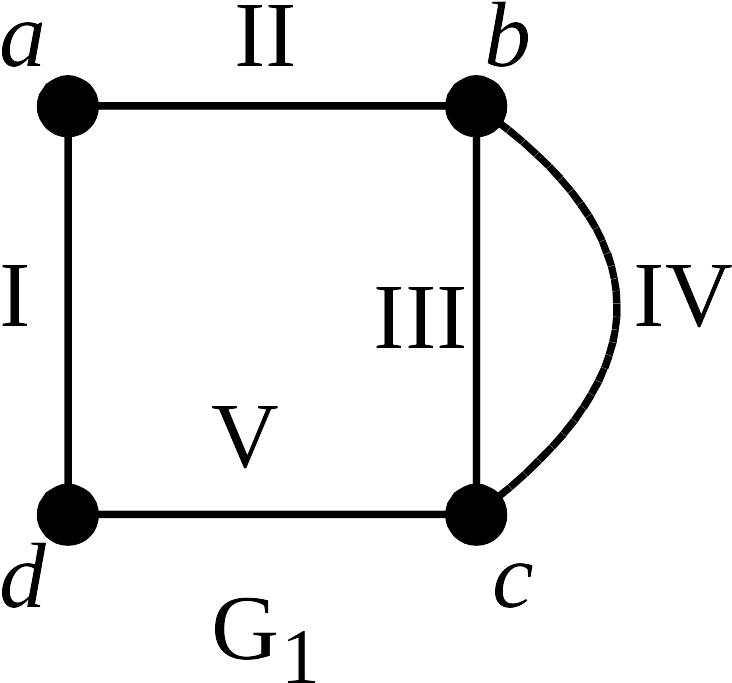 ример 1. На рисунке изображены три геометрических графа.

Покажем, что графы и неизоморфны. Будем рассуждать от противного. Предположим, что эти графы изоморфны. Тогда существует пара задающих изоморфизм отображений , так что

и .

То есть при изоморфизме образами кратных ребер графа должны быть кратные ребра. Но кратных ребер в графе нет. Следовательно, наше предположение об изоморфизме графов и неверно.

Покажем, что графы и изоморфны. Определим отображения следующим образом: , , , , , , , , . Надо показать, что для каждого ребра графа , если то

Вначале проверим выполнение этого условия для ребра графа , т.е. покажем, что высказывание истинно.

Действительно, с учетом того, что , , , вместо можем записать , что верно (см. рис.).

Аналогичную проверку делаем и для остальных ребер графа .

5. Операции над графами.

Пусть - произвольный неориентированный граф, а - его подграф. С каждой вершиной и каждым ребром графа можно связать подграфы , и .

1. Подграф получается из подграфа удалением вершины и всех инцидентных этой вершине ребер. Отметим, что если не входит в множество вершин графа , то .

2. Подграф получается из подграфа удалением ребра и всех инцидентных этой вершине ребер. Если не входит в множество ребер графа , то .

3. Подграф получается из подграфа добавлением ребра и двух его концевых вершин. Если входит в множество ребер графа , то .

4. Говорят, что граф получен из графа путем подразбиения ребра , если

,

, ,

, , где - концы ребра .

П ример 2.

- граф, полученный из графа путем подразбиения ребра .

Пусть и - подграфы графа .

6. Пересечением графов и называется граф .

7. Объединением графов и называется граф .

Аналогично определяется пересечение и объединение любого конечного числа подграфов.

Определение. Пусть , ,…, - непустые подграфы графа и выполнены условия:

1. ;

2. .

Тогда семейство множеств называется дизъюнктным разбиением графа .

6. Матрица смежности ориентированного графа. Примеры.

. Матрицей смежности орграфа называется матрица размера , элементы которой , где - число дуг, исходящих из вершины с номером и заходящих в вершину с номером .

7. Эйлеров цикл. Определение, критерий существования.

Определение. Цикл на графе называется эйлеровым циклом, если он содержит все вершины и все ребра графа.

Определение. Граф, на котором имеется эйлеров цикл, называется эйлеровым графом.

Пример 1. Рассмотрим граф : , , , , . Цикл эйлеров. Следовательно, - эйлеров граф.

Лемма. Если степень каждой вершины связного графа четна, то он содержит хотя бы один цикл.

Доказательство. Так как степени вершин графа четные, то . Имеем:

.

Так что , и, значит, . Следовательно, согласно основной теореме о деревьях граф не может быть деревом, а, значит, на графе имеется хотя бы один цикл. ■

Теорема (критерий эйлеровости графа). Ненулевой граф является эйлеровым в том и только в том случае, если он связен и каждая его вершина имеет четную степень.

8. Кодирование и декодирование, криптология и криптография, кодирующее устройство.

Кодирование информации это преобразование формы представления информации с целью ее передачи или хранения. Кодирование это представление символов одного алфавита символами другого. Правила, по которым осуществляется кодирование называются кодом. Под словом понимают последовательность символов,. количество символов в которой называется длиной кода. Слова так же называют кодовыми комбинациями. Если при кодировании получают комбинации одинаковой длины, то такой код называют равномерным, а длину кодовых комбинаций в этом слове называют значимостью кода. Если кодовые комбинации различной длины, то код называется неравномерным. Процесс обратный кодированию называется декодированием. Если в коде ни одна более короткая комбинация не является началом более длинной кодовой комбинации, то код называется префиксным.

Криптология - наука, занимающаяся методами шифрования и дешифрования. Криптология состоит из двух частей —криптографии и криптоанализа. Криптография занимается разработкой методов шифрования данных, в то время как криптоанализ занимается оценкой сильных и слабых сторон методов шифрования, а также разработкой методов, позволяющих взламывать криптосистемы.

Криптография - наука о методах обеспеченияконфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации.

Изначально криптография изучала методы шифрования информации — обратимого преобразования открытого (исходного) текста на основе секретного алгоритма и/или ключа в шифрованный текст (шифротекст). Традиционная криптография образует раздел симметричных криптосистем, в которых зашифрование и расшифрование проводится с использованием одного и того же секретного ключа. Помимо этого раздела современная криптография включает в себя асимметричные криптосистемы,системы электронной цифровой подписи (ЭЦП), хеш-функции, управление ключами,получение скрытой информации, квантовую криптографию.

9. Построение алфавитного кодирования. Примеры.