Оператор суперпозиции

Функция hⁿ(x₁, ..., x_n) получается из функций g^m, fⁿ₁, ..., fⁿ_m с помощью оператора суперпозиции, если hⁿ(x₁, ..., x_n) = g^m(fⁿ₁(x₁, ..., x_n), ..., fⁿ_m(x₁, ..., x_n)).

П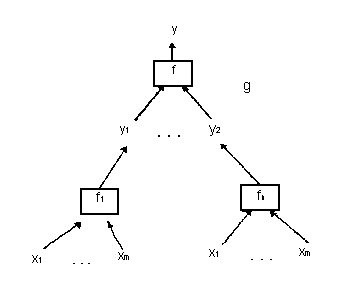 онятно, что функция g^m (x₁, х₂, ... ,x_m) и есть та функция, которую определяет функциональный терм fⁿ (f₁^m(x₁, х₂, ... ,x_m),..., f_n^m (x₁, х₂, ... ,x_m)) при соответствующей интерпретации (рис. 2.2).

(Рис. 2.2)

Таким образом, функция g = Sⁿ⁺¹(f, f₁,..,f_n) определятся/вычисляется функциональным термом (рис. 2.2). И наоборот, функциональному терму соответствует применение некоторого оператора суперпозиции. Переменные y₁, у₂, .. ,y_m представляют промежуточные величины.

Пусть φⁿ - множество всех частичных вычислимых функций от n переменных. Тогда оператор суперпозиции Sⁿ⁺¹ может рассматриваться как всюду определенная функция Sⁿ⁺¹ : φⁿxφ^mxφ^mx...xφ^m → φ^m. Теперь в этих терминах можно перефразировать понятие функции, полученной применением оператора суперпозиции, а именно:

функция g(x₁, х₂, ... ,x_m) получается суперпозицией из функций f(x₁, х₂, ... ,x_n), f₁(x₁, х₂, ... ,x_m),..., f_n^m (x₁, х₂, ... ,x_m) , если g есть значение операторного терма Sⁿ⁺¹ (h, h₁, ..., h_n), где h, h₁, ..., h_n - переменные и интерпретация ставят в соответствие:

• переменной h – значение f, элемент из φⁿ,

• переменным h,h₁, ..., h_n - значения f_i из φ^m соответственно, i = 1,2,..., n,

• функциональному символу Sⁿ⁺¹ - функцию f(f₁(x₁, х₂, ... ,x_m),..., f_n (x₁, х₂, ... ,x_m))= g(x₁, х₂, ... ,x_m).

Таким образом, можно использовать либо операторную, либо термальную запись представления функции g. В первой из них g есть значение операторного терма, во второй g определяется как функциональный терм. Этот функциональный терм и определяет алгоритм вычисления функции g.

9.Оператор примитивной рекурсии, алгоритм его вычисления

Оператор примитивной рекурсии:

Функция fⁿ⁺¹(x₁, ..., x_n, y) получается из функций gⁿ(x₁, ..., x_n) и hⁿ⁺²(x₁, ..., x_n, y, z) с помощью оператора примитивной рекурсии, если она может быть задана схемой примитивной рекурсии:

fⁿ⁺¹(x₁, ..., x_n, 0) = gⁿ(x₁, ..., x_n),

fⁿ⁺¹(x₁, ..., x_n, y+1) = hⁿ⁺²(x₁, ..., x_n, y, fⁿ⁺¹(x₁, ..., x_n, y)). (1)

Соотношения (1) называются схемой примитивной рекурсии. Они определяют оператор примитивной рекурсии R. Эта схема, собственно, и есть алгоритм вычисления функции f. Оператор определен на множестве φ частичных вычислимых функций, f = R(g,h).

Если n = 0, то одноместная функция f строится примитивной рекурсией из функции-константы Cnst (это просто некоторое натуральное число) и двухместной функции h

f(0)= Cnst, f(x+l)= h(x,f(x₁)).

Понятно, что функция f существует и единственна. Это следует из того, что определение функции, построенной примитивной рекурсией, фактически содержит схему (алгоритм) ее вычисления. Распишем детально эту схему, используя термальные представления.

Пусть необходимо вычислить значение функции f при у = k. Тогда из определения (1) схемы примитивной рекурсии имеем последовательность функциональных термов, вычисляющих значение функции f(x₁, х₂, ... ,x_n, k):

t_o: f_o=f(x₁, х₂, ... ,x_n, 0) =g(x₁, х₂, ... ,x_n);

t₁: f₁=f(x₁, х₂, ... ,x_n, 1) =h(x₁, х₂, ... ,x_n, 0, g(x₁, х₂, ... , x_n));

t₂: f₂=f(x₁, х₂, ... ,x_n, 2) =h(x₁, х₂, ... ,x_n, 1, f(x₁, х₂, ... , x_n, 1));

......................................

t_k: f_k=f(x₁, х₂, ... ,x_n, k) =h(x₁, х₂, ... ,x_n, k-1, f(x₁, х₂, ... , x_n, k-1));

Здесь представлен способ вычисления f, следовательно, функция f определена однозначно. Эту последовательность k+1 функциональных термов t_o, t₁,... удобно для наглядности изобразить графически

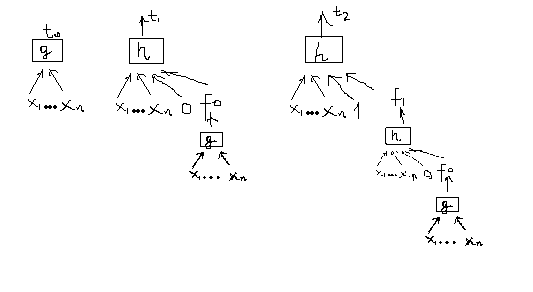
Это множество функциональных термов и определяет, собственно, алгоритм вычисления функции f. Множество термов (представление алгоритмов в виде множества термов) позволяет легко построить программу Р, реализующую оператор суперпозиции и вычисляющую функцию f:

f(x1,…,xn, xk) -?

P:

s=k-1;

f[0]=g(x1,…,xn);

for(i=1; i<s; i++);

f[i]=h(x1,…,xn,i-1,f[i-1]);

(рис 1)

Таким образом, алгоритм вычисления функции f задан применением оператора примитивной рекурсии. Функций g и h задаются функционально ∞ множеством функциональных термов.

Функционально ∞ множество – это множество, которое в каждом случае конечно, но не ограниченно.

(пример, файл)