
алгоритмы на графах ответы на вопросы vkclub152685050
.pdf
Контакты
vk.com/id446425943
vk.com/club152685050
Что такое граф?
Граф абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.
Какие алгоритмы обхода графа существуют?
При решении многих задач, касающихся графов, необходимы эффективные методы систематического обхода вершин и ребер графов.
алгоритмы обхода графа |
vk.com/club152685050 |
|
• |
поиск в глубину; |
vk.com/id446425943 |
• |
поиск в ширину. |
|
Эти методы чаще всего рассматриваются на ориентированных графах, но они применимы и для неориентированных, ребра которых считаются двунаправленными
Поиск в глубину
Предположим, что есть ориентированный граф G, в котором первоначально все вершины помечены как непосещенные. Поиск в глубину начинается с выбора начальной вершины v графа G, и эта вершина помечается как посещенная. Затем для каждой вершины, смежной с вершиной v и которая не посещалась ранее, рекурсивно применяется поиск в глубину. Когда все вершины, которые можно достичь из вершины v, будут «удостоены» посещения, поиск заканчивается. Если некоторые вершины остались не посещенными, то выбирается одна из них и поиск повторяется. Этот процесс продолжается до тех пор, пока обходом не будут охвачены все вершины орграфа G.
Поиск в глубину для полного обхода графа с n вершинами и m дугами требует общего времени
порядка O(max(n, m)). Поскольку обычно m ≥ n, то получается O(m).
Поиск в ширину (Волновой алгоритм
Этот алгоритм поиска в графе также называют волновым алгоритмом из-за того, что обход графа идет по принципу распространения волны. Волна растекается равномерно во все стороны с одинаковой скоростью.
Метод поиска в ширину получается из программы поиска в глубину если заменить стек возврата на очередь. Эта простая замена модифицирует порядок обхода вершин так, что обход идет равномерно во все стороны, а не вглубь как при поиске в глубину
Поиск в ширину для полного обхода графа с n вершинами и m дугами требует столько же времени, как и поиск в глубину, т. е. Времени порядка O(max(n, m)). Поскольку обычно m ≥ n, то получается
O(m).

Какие алгоритмы нахождения кратчайшего пути в графе существуют?
Нахождение кратчайшего пути |
vk.com/club152685050 |
|
• |
Алгоритм Дейкстры |
|
• |
Алгоритм Флойда |
vk.com/id446425943 |
Алгоритм Дейкстры
Этот алгоритм находит в графе кратчайший путь из заданной вершины, определенной как источник, во все остальные вершины. процессе своей работы алгоритм строит множество S вершин, для которых кратчайшие пути от источника уже известны. На каждом шаге к множеству S добавляется та из оставшихся вершин, расстояние до которой от источника меньше, чем для других оставшихся вершин. При этом используется массив D, в который записываются длины кратчайших путей для каждой вершины. Когда множество S будет содержать все вершины графа, тогда массив D будет содержать длины кратчайших путей от источника к каждой вершине.
Для определения самого кратчайшего пути (т. е. Последовательности вершин) необходимо ввести еще один массив P вершин, где P[v] содержит вершину, непосредственно предшествующую вершине v в кратчайшем пути
После выполнения алгоритма кратчайший путь к каждой вершине можно найти с помощью обратного прохождения по предшествующим вершинам массива P, начиная от конечной вершины к источнику.
Время выполнения этого алгоритма, если для представления графа используется матрица смежности, имеет порядок O(n2), где n – количество вершин графа.
Алгоритм Флойда
Этот алгоритм решает задачу нахождения кратчайших путей между всеми парами вершин графа. Более строгая формулировка этой задачи следующая: есть ориентированный граф G = (V, Е), каждой дуге (v, w)этогографасопоставленанеотрицательнаястоимостьC[v,w].Общаязадачанахождения) этого графа сопоставлена неотрицательная стоимость C[v, w)этогографасопоставленанеотрицательнаястоимостьC[v,w].Общаязадачанахождения]. Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин (v, w)этогографасопоставленанеотрицательнаястоимостьC[v,w].Общаязадачанахождения) любого пути из вершины v в вершину w)этогографасопоставленанеотрицательнаястоимостьC[v,w].Общаязадачанахождения, длина которого минимальна среди всех возможных путей из вершины v к w)этогографасопоставленанеотрицательнаястоимостьC[v,w].Общаязадачанахождения.
Можно решить эту задачу, последовательно применяя алгоритм Дейкстры для каждой вершины, объявляемой в качестве источника. Но существует прямой способ решения данной задачи, использующий алгоритм Флойда. Для определенности положим, что вершины графа последовательно пронумерованы от 1 до n. Алгоритм Флойда использует матрицу A размера n×n, в которой вычисляются длины кратчайших путей. В начале A[i, j] = C[i, j] для всех i < > j. Если дуга (i, j) отсутствует, то C[i, j] = ∞. Каждый диагональный элемент матрицы A равен 0
Над матрицей A выполняется n итераций. После k-й итерации A[i, j] содержит значение наименьшей длины путей из вершины i в вершину j, которые не проходят через вершины с номером, большим k.
Другими словами, между концевыми вершинами пути i и j могут находиться только
вершины, номера которых меньше или равны k На k-й итерации для вычисления матрицы A

vk.com/club152685050
vk.com/id446425943
применяется следующая формула: Аk[i, j] = min(Ak–1[i, j], Ak–1[i, k] + Ak–1[k, j]). Нижний индекс k обозначает значение матрицы А после k-й итерации, но это не означает, что существует n различных матриц, этот индекс используется для сокращения записи. Равенства Ak[i, k] = Ak–1[i, k] и Ak[k, j] = Ak–1[k, j] означают, что на k-й итерации элементы матрицы A, стоящие в k-й строке и k-м столбце,
не изменяются. Более того, все вычисления можно выполнить с применением только одного экземпляра матрицы A
Какие переборные алгоритмы нахождения кратчайшего пути в графе существуют?
Перебор методом поиска в глубину Перебор методом поиска в ширину
Перебор методом поиска в глубину
Метод перебора с возвратом (по-английски называемый backtracking)) основан на методе поиска в глубину. Перебор с возвратом – это метод проб и ошибок («попробуем сходить в эту сторону: не получится – вернемся и попробуем в другую»). Поскольку речь идет о переборе вариантов методом поиска в глубину, то во время работы алгоритма надо хранить текущий путь в дереве. Этот путь представляет собой стек Way. Кроме того, необходим массив Dest, размерность которого соответствует количеству вершин графа, хранящий для каждой вершины расстояние от нее до исходной вершины
Перебор методом поиска в ширину |
vk.com/club152685050 |
|
vk.com/id446425943 |
||
|
Переборный алгоритм, основанный на поиске в ширину, состоит из двух этапов:
1)распространение волны;
2)обратный ход.
Распространение волны и есть собственно поиск в ширину при котором клетки помечаются номером шага метода, на котором клетка посещается. При обратном ходе, начиная с конечной вершины, идет восстановление кратчайшего пути, по которому в нее попали путем включения в него клеток с минимальной пометкой Важно, что восстановление начинается с конца Надо сказать, что перебор методом поиска в ширину по сравнению с перебором с возвратом, как правило, требует больше дополнительной памяти, расходуемой на хранение информации нужной для построения пути при обратном ходе и пометки посещенных вершин, но и работает быстрее, так как совершенно исключается посещение одной и той же клетки более, чем один раз.
Какие алгоритмы нахождения минимального остовного дерева графа существуют?
Приведем без доказательства следующее свойство MST (minimal spanning) tree – минимальное остовное дерево на английском языке).
алгоритмы нахождения минимального остовного дерева
•Алгоритм Прима
•Алгоритм Крускала
vk.com/club152685050
vk.com/id446425943
Алгоритм Прима
В этом алгоритме строится множество вершин U, из которого «вырастает» остовное дерево
Сначала U = .Накаждомшагеалгоритманаходитсяребронаимень. На каждом шаге алгоритма находится ребро наименьшей стоимости (u, v) такое, что u
U,v V\U, U, v U,v V\U, V\U, затем вершина v переносится из V\U в U. Этот процесс продолжается до тех пор, пока множество U не станет равным множеству V
Очевидно, данный алгоритм для графа с n вершинами имеет сложность, пропорциональную O(n2)
Алгоритм Крускала
Здесь построение MST начинается с графа, состоящего только из n вершин графа G и не имеющего ребер. Таким образом, каждая вершина является связанной (сама с собой) компонентой. Это дает n связанных компонентов. В процессе выполнения алгоритма связанные компоненты постепенно
объединяются друг с другом, формируя остовное дерево
При построении постепенно возрастающих связанных компонент поочередно проверяются ребра из множества E в порядке возрастания их длин. Если очередное ребро связывает две вершины из разных компонент, тогда оно добавляется в остовное дерево. Если это ребро связывает две вершины из одной компоненты, то оно отбрасывается, так как его добавление в связанную компоненту может
привести к образованию цикла. Число ребер, необходимое для остовного дерева равно n–1. Граф связан, а значит E содержит как минимум такое их количество.
Сложность алгоритма для графа с n вершинами и m ребрами пропорциональна O(mlog m).
vk.com/club152685050
vk.com/id446425943
vk.com/id446425943
vk.com/club152685050 ЛАБОРАТОРНАЯ РАБОТА №7
«АЛГОРИТМЫ НА ГРАФАХ»
1.1 Цель работы
Целью работы является изучение графов и получение практических навыков их использования. vk.com/club152685050
vk.com/id446425943
1.2 Задание на лабораторную работу
Разработать на языке программирования высокого уровня программу, которая должна выполнять функцию, в соответствии с вариантом задания. Варианты задания приведены в таблице 7 (формулировки задач приведены после таблицы).
Количественные параметры варианта задания определяются по согласованию с преподавателем.
Таблица 1
№ |
Задача |
Представление графа |
|
вар. |
|||
|
|
||
1 |
1 |
Матрица смежности |
|
2 |
1 |
Матрица инцидентности |
|
3 |
1 |
Список ребер |
|
4 |
2 |
Матрица смежности |
|
5 |
2 |
Матрица инцидентности |
|
6 |
2 |
Список ребер |
|
7 |
3 |
Матрица смежности |
|
8 |
3 |
Матрица инцидентности |
|
9 |
3 |
Список ребер |
|
10 |
4 |
Матрица смежности |
|
11 |
4 |
Матрица инцидентности |
|
12 |
4 |
Список ребер |
|
13 |
5 |
Матрица смежности |
|
14 |
5 |
Матрица инцидентности |
|
15 |
5 |
Список ребер |
|
16 |
6 |
Матрица смежности |
|
17 |
6 |
Матрица инцидентности |
|
18 |
6 |
Список ребер |
|
19 |
7 |
Матрица смежности |
|
20 |
7 |
Матрица инцидентности |
|
21 |
7 |
Список ребер |
|
22 |
8 |
Матрица смежности |
|
23 |
8 |
Матрица инцидентности |
|
24 |
8 |
Список ребер |
vk.com/club152685050
vk.com/id446425943
Задача 1.
Прямоугольное изображение задано графом, так что каждая вершина является пикселем изображения, ребра соединяют соседние пиксели по горизонтали и вертикали. Требуется:
1)проверить соответствует ли описанный граф изображению (нет пропущенных пикселей);
2)Найти и «закрасить» замкнутые контура на изображении.
Задача 2.
На случай экстренной ситуации на предприятии имеется список сотрудников и список оповещения вида: (фамилия оповещающего, фамилия оповещаемого). Один оповещающий может оповестить за день 3 человек. Определить:
1) полон ли список оповещения, то есть будут ли оповещены все сотрудники;
2) сколько людей будет оповещено за K дней.
Задача 3.
Задача Эйлеровых циклов. Дан граф, требуется определить, возможно ли пройти из указанной вершины по всем ребрам графа, и, если возможно, указать данный путь.
Задача 4.
Найти все возможные пути между двумя вершинами в графе, не пересекающиеся по:
а) pебpам;
б) вершинам.
Задача 5.
Решить 2 задачи:
1.Задача о минимальном вершинном покрытии;
2.Задача о минимальном рѐберном покрытии.
Задача 6.
Составить программу для нахождения произвольного разбиения N студентов на M команд, численность которых отличается не более чем в 2 раза, если известно, что в любой команде должны быть студенты, обязательно не знакомые друг с другом. Круг знакомств задается графом, где вершина – это студент, а ребро отображает его знакомство с другим студентом. Решить задачи:
2
vk.com/club152685050
vk.com/id446425943
1)Определить наименьшее количество команд, на которое можно разбить множество студентов;
2)Проверить возможность разбиения множества студентов на заданное количество команд.
Задача 7.
В помещении присутствует N человек. Некоторые из них знакомы между собой. Проверить, можно ли перезнакомить людей между собой? (Незнакомые люди могут познакомиться только через общего знакомого).
Задача 8.
Дано N колец сцепленных между собой. Удалить минимальное количество колец так, чтобы получилась цепочка.
1.3Порядок выполнения работы
1)выбрать вариант задания в соответствии с требованиями;
2)изучить теоретический материал;
3)разработать и реализовать на языке программирования высокого уровня алгоритм, выполняющий требования задания;
4)написать отчет о работе;
5)защитить отчет.
1.4Содержание отчета
Отчет должен содержать:
1)титульный лист;
2)цель работы;
3)вариант задания;
4)листинг программы, реализующей алгоритм;
5)контрольный пример с изображением графа;
6)выводы по работе.
|
|
|
vk.com/club152685050 |
|
1.5 Пример выполнения работы |
vk.com/id446425943 |
|
Предположим, что необходимо выполнить следующий вариант |
|||
задания: |
|
|
|
|
|
|
|
№ вар. |
Задача |
|
Представление графа |
25 |
9 |
Матрица смежности |
|
3
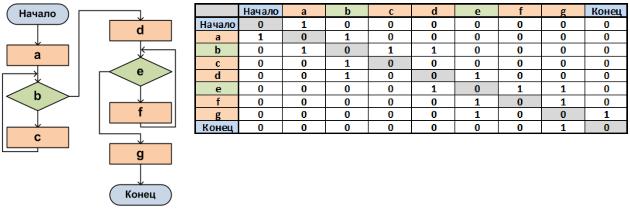
Задача 9.
Дана схема алгоритма. Определить по схеме достижимость конечной вершины из начальной.
Дополнительные указания: схема алгоритма – ориентированный граф, возможно содержащий циклы. Воспользоваться волновым алгоритмом
Для решения поставленной задачи необходимо построить граф, используя заданное представление, а затем применить рекомендуемый алгоритм.
Пусть задана схема алгоритма (см. Рисунок). На основе нее строим матрицу смежности (см. Рисунок). Теперь можно воспользоваться волновым алгоритмом, взяв за исходную вершину – вершину "Начало". По окончании работы алгоритма остается проверить, была ли помечена как пройденная вершина "Конец". Если вершина "Конец" была помечена, то можно сделать вывод, что конечная вершина достижима, в противном случае – конечная вершина не достижима.
Следует отметить, что граф может иметь циклы, однако для волнового алгоритма их наличие не является опасным.
Рисунок vk.com/club152685050 vk.com/id446425943
1.6Контрольные вопросы
1)Что такое граф?
2)Назовите основные способы реализации графа. Сравните их.
3)Какие алгоритмы обхода графа существуют? Какова их временная сложность?
4
4)Какие алгоритмы нахождения кратчайшего пути в графе существуют? Какова их временная сложность?
5)Какие переборные алгоритмы нахождения кратчайшего пути в графе существуют? Какова их временная сложность?
6)Какие алгоритмы нахождения минимального остовного дерева графа существуют? Какова их временная сложность?
vk.com/club152685050
vk.com/id446425943
5
