Аудиторная самостоятельная работа №1

Уравнение линии на плоскости. Уравнение прямой на плоскости. Общее уравнение прямой, частные случаи общего уравнения прямой. Канонические и параметрические уравнения прямой. Уравнение прямой, проходящей через две точки. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Понятие об уравнении линии на плоскости

Рассмотрим на плоскости декартову прямоугольную систему координат . Пусть на этой плоскости задана некоторая линия .

Определение 1

Уравнение называется уравнением линии , если этому уравнению удовлетворяют координаты и любой точки, лежащей на линии, и не удовлетворяют координаты и ни одной точки, не лежащей на линии .

Замечание

Из определения следует, что линия является геометрическим местом точек, координаты которых удовлетворяют уравнению .

Определение 2

Переменные и в уравнении линии называются текущими координатами точек линии.

Определение 3

Если текущие координаты выражены при помощи параметра , т. е

,

то говорят, что линия задана параметрически.

В аналитической геометрии на плоскости рассматриваются две основные задачи:

• изучение свойств линии при помощи заранее данного уравнения этой линии;

• вывод уравнения линии по ее геометрическим свойствам.

Уравнения прямой на плоскости

Нормальный вектор прямой. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Рассмотрим на плоскости произвольную прямую . Пусть дана некоторая точка этой прямой и вектор , перпендикулярный рассматриваемой прямой (рис. 2).

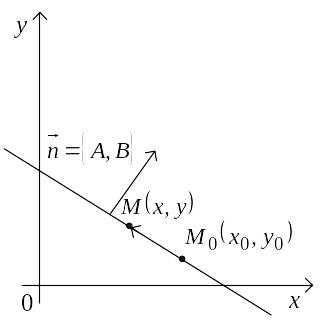
Рис. 2

Определение

Любой ненулевой вектор, перпендикулярный прямой, называется нормальным вектором этой прямой.

Точка и нормальный вектор вполне определяют положение прямой на плоскости . Пусть точка - любая точка прямой . Рассмотрим вектор , лежащий на этой прямой. Нормальный вектор по определению перпендикулярен . Следовательно, их скалярное произведение равно нулю: . Записывая последнее уравнение в координатах, имеем

. (1)

Полученному уравнению удовлетворяют координаты любой точки, принадлежащей прямой . Если точка плоскости не лежит на прямой , то , и координаты точки не удовлетворяют уравнению.

Уравнение (1) называется уравнением прямой, проходящей через данную точку перпендикулярно заданному вектору.

Общее уравнение прямой

Рассмотрим теперь уравнение первой степени

. (2)

Это уравнение заведомо имеет хотя бы одно решение , т. е. существует хотя бы одна точка , координаты которой удовлетворяют уравнению (2):

. (3)

Вычитая из уравнения (2) тождество (3), получаем уравнение

.

Таким образом, уравнение первого порядка, в котором хотя бы один из коэффициентов или не равен нулю, определяет некоторую прямую в плоскости .

Уравнение (2) называется общим уравнением прямой.

Неполные уравнения прямой. Уравнение прямой в отрезках

Уравнение прямой (2) называется неполным, если хотя бы один из коэффициентов , или равен нулю.

• Пусть . Уравнение прямой принимает вид

.

Такому уравнению удовлетворяют координаты начала , . Следовательно, описанная прямая проходит через начало координат.

• Пусть . Тогда имеем уравнение прямой

с нормальным вектором , ортогональным оси .

Следовательно, полученное уравнение определяет прямую, параллельную оси .

• Пусть . Тогда имеем уравнение прямой

с нормальным вектором , ортогональным оси . Следовательно, полученное уравнение определяет прямую, параллельную оси .

• Пусть и . Полученная прямая

задает ось .

• Пусть и . Полученная прямая

задает ось .

Рассмотрим полное уравнение прямой . Так как все коэффициенты , и отличны от нуля, то можно записать это уравнение в следующем виде:

.

Положим теперь

, .

Полученное уравнение

называется уравнением прямой в отрезках.

Точками пересечения этой прямой с координатными осями будут точки и . Нормальный вектор .

Уравнение прямой в отрезках удобно использовать при построении прямой на чертеже (рис. 3).

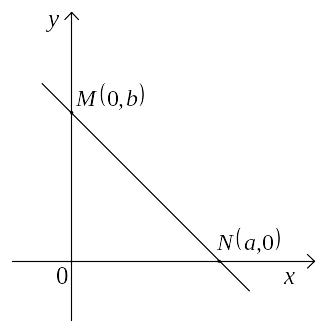
Рис. 3

Каноническое уравнение прямой

Рассмотрим на плоскости произвольную прямую . Пусть дана некоторая точка этой прямой и вектор , параллельный рассматриваемой прямой (рис. 4).

Рис. 4

Определение

Любой ненулевой вектор, параллельный прямой, называется направляющим вектором этой прямой.

Точка принадлежит прямой тогда и только тогда, когда векторы и коллинеарны, т. е. выполнено условие

пропорциональности координат этих векторов:

. (4)

Уравнение (4) называется каноническим уравнением прямой

Замечание

В каноническом уравнении один из знаменателей или может оказаться равным нулю. Понимая уравнение (4) как пропорцию, получаем, например при , что , т. е. (уравнение прямой, параллельной оси ). Аналогично, при получаем уравнение прямой параллельной оси .

Уравнение прямой, проходящей через две точки

Пусть даны две точки и . Составим каноническое уравнение прямой, проходящей через эти точки. В качестве направляющего вектора выберем вектор . Тогда по формуле (4) имеем

. (5)

Пример

Написать уравнение прямой, проходящей через точки и . Привести это уравнение к общему виду.

Решение

Полагая в формуле (5) , , , , получаем , откуда или . В общем виде уравнение можно записать, используя свойство пропорции: , откуда

.

Параметрические уравнения прямой

Выразим текущие координаты через параметр . Для этого в каноническом уравнении (4) примем обе его части за , откуда

.

Эти уравнения называются параметрическими. Областью изменения параметра является вся числовая ось: .

Уравнение прямой с угловым коэффициентом

Рассмотрим на плоскости произвольную прямую , не параллельную оси .

Под углом наклона прямой понимают угол между положительным направлением оси и прямой (рис. 5).

Рис. 5.

Положение прямой вполне определяется заданием угла и точки, лежащей на этой прямой. Пусть это точка . В качестве направляющего вектора возьмем единичный вектор , составляющий с осью тот же угол , что и прямая. Так как , если - острый угол, и , если - тупой угол, то , и . Составляя каноническое уравнение прямой, запишем

.

Разрешая это уравнение относительно , получим

Обозначим . Тогда

. (6)