68. Формулировка теоремы Котельникова. Спектр дискретизованного сигнала.

В теории и технике сигналов широко используется теорема Котельни­кова (теорема отсчетов): если наивысшая частота в спектре функции s (t) меньше, чем f_т, то функция s (t) полностью определяется последовательно­стью своих значений в моменты, отстоящие друг от друга не более чем на 1/2f_т секунд.

В соответствии с этой теоремой сигнал s(t), ограниченный по спектру наивысшей частотой 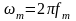, можно представить рядом

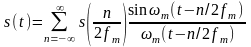. (1.166)

В этом выражении 1/2f_m = Δt обозначает интервал между двумя отсчетными точками на оси времени, а s(n/2f_m) = s (nΔt) — выборки функции s(t) в моменты времени t = nΔt.

Представление заданной функции s(t) рядом (1.166) иллюстрируется рис. 1.24.

Рис. 1.24. Представление сигнала рядом Котельникова

Спектр дискретного сигнала. Преобразование Фурье правой части выражения (1.161) определяет спектральную плотность S_д(j2f) дискретного сигнала

S_д(j2f) = 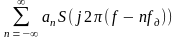, –  < f < , (1.164)

где f_д = 1/ T_д – частота дискретизации;

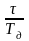
a_n = 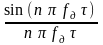 – (1.165)

коэффициенты разложения последовательности импульсов h(t) в ряд Фурье; поскольку  << T_д, то для малых значений n коэффициенты практически не зависят от n, то есть a_n = /Т_д;

S(j2f) – спектральная плотность непрерывного сигнала s(t).

Из (1.164) следует, что спектр дискретного сигнала – это сумма спектров S(j2f) непрерывного сигнала s(t), смещенных один относительно другого на величину f_д и убывающих с увеличением n в соответствии с выражением (1.165).

Далее на рис. 1.23 изображены амплитудные спектры сигналов, которые могут иметь место при дискретизации сигнала со спектром, приведенным на

рис. 1.23, а - амплитудный спектр произвольной формы S(f);

рис. 1.23, б – спектр S_(f) последовательности отсчетных импульсов (t), построенный на основе представления (t) рядом Фурье:

(t) = 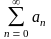cos(2nf_дt);

рис.1.2 3, в – спектр S_д(f) дискретного сигнала, если f_д > 2F_max;

рис. 1.23, г – спектр S_д(f), если f_д = 2F_max;

рис. 1.23, д – спектр S_д(f), если f_д < 2F_max.

69. Дискретное преобразование Фурье и его основные свойства.

Воспользуемся моделью в виде последовательности дельта-импульсов и сопоставим исходному колебанию x(t) его дискретное МИП-представление:

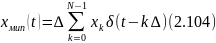
Представим дискретную модель (2.104) комплексным рядом Фурье:

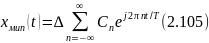
с коэффициентами

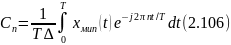
Подставляя формулу (12.104) в (2.106) и вводя безразмерную переменную , получим

.

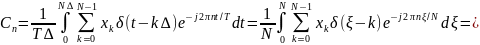
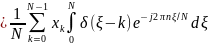Наконец, используя фильтрующее свойство дельта-функции, имеем

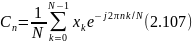
Формула (2.107) определяет последовательность коэффи­циентов образующих дискретное преобразование Фурье (ДПФ) рассматриваемого сигнала. Отметим некоторые очевидные свойства ДПФ.

1. Дискретное преобразование Фурье есть линейное преоб­разование, т. е. сумме сигналов отвечает сумма их ДПФ.

2. Число различных коэффициентов 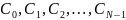, вычисляемых по формуле (2.107), равно числу N отсчетов за период; при п = N коэффициент C_N = С₀.

3. Коэффициент С₀ (постоянная составляющая) является средним значением всех отсчетов:

.

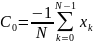4. Если N — четное число, то

.

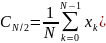5. Пусть отсчетные значения х_к — вещественные числа. Тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряженные пары:

.

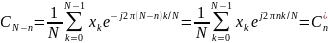Поэтому можно считать, что коэффициенты 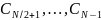отвечают отрицательным частотам. При изучении амплитуд­ного спектра сигнала они не дают новых сведений.