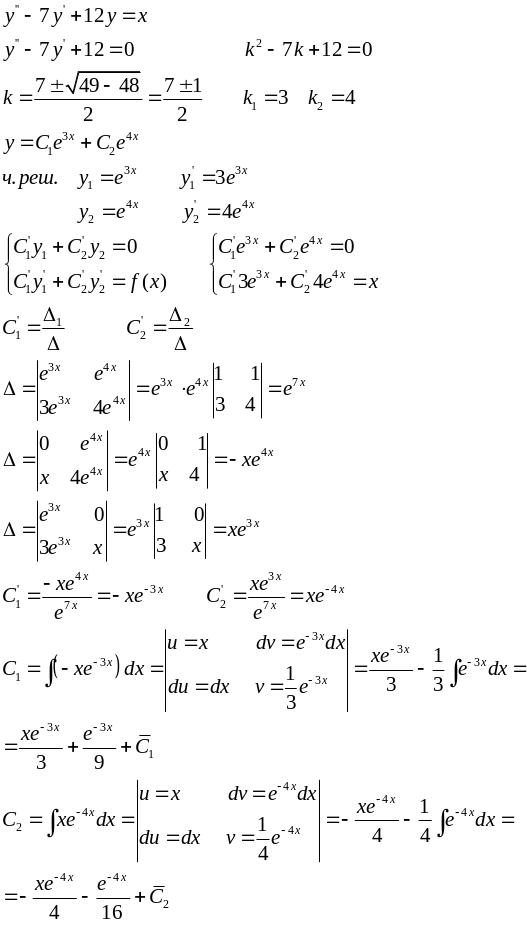- •4. Дифференциальные уравнения высших порядков.
- •6.Интегрирование простейших типов уравнений второго порядка методом понижения порядка.
- •8. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •§9 Линейные однородные уравнения n-го порядка с постоянными коэффициентами.
- •§11. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами.
- •§12 Неоднородные линейные уравнения высших порядков
8. Линейные однородные уравнения второго порядка с постоянными коэффициентами
Имеем линейное однородное уравнение второго порядка
![]() (1)
(1)
где a1, a2 – постоянные действительные числа.
Будем искать частные решения в виде
![]() , где k-const
(2)
, где k-const
(2)
Тогда ![]() ,
, ![]()
Подставляя в данное уравнение, получим
![]()
т. к. ![]() ,
то
,
то ![]() (3)
(3)
Следовательно, если k удовлетворяет уравнению (3), то функция (2) будет решением уравнения (1). Уравнение (3) называют характеристическим уравнением по отношению к уравнению (1).
Корни характеристического уравнения (3).
![]()
![]()
Возможны следующие случаи:
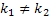 -
действительные и не равные между собой
числа.
-
действительные и не равные между собой
числа. - действительные равные числа.
- действительные равные числа. - комплексные числа.
- комплексные числа.
Рассмотрим каждый случай в отдельности.
Корни характеристического уравнения действительны и различны:
В этом случае имеется частные решения
![]()
![]()
![]()
![]() – два линейно независимых частных
решения.
– два линейно независимых частных
решения.
О
![]()
2) Корни характеристического уравнения действительные и равные:
Частные решения
и
линейно зависимы, т. к. ![]()
Будем искать частное решение ![]() в виде
в виде ![]()
где ![]() - неизвестная функция
- неизвестная функция
Подставим ее в уравнение (1)
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Т.к. k1=k2, то 2k1= - a; 2k1+a1=0
(k1
– корень уравнения (3)), то
![]()
Получим
![]() .
.
Решая, будим иметь:
![]() u=Ax+B,
где A,
B
– const.
u=Ax+B,
где A,
B
– const.
Нам достаточно знать одну из ф-ий u(x).
Пусть А=1, B=0, тогда u(x)=x.
Частное решение
![]() :
:
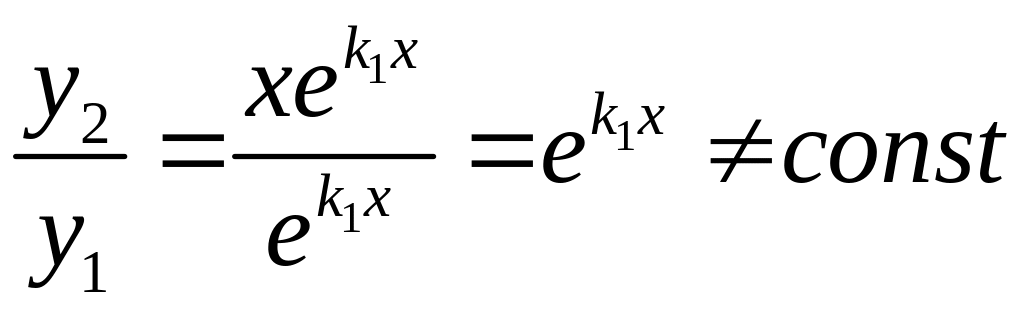 .
.
Общее решение будет:
![]() ,
,
или
![]() .
.
3) Корни характеристического уравнения комплексные
![]() .
.
Комплексные корни
попарно сопряжённые, обозначим их:
![]() ,
,
![]() ,
,
где
![]() ,
,
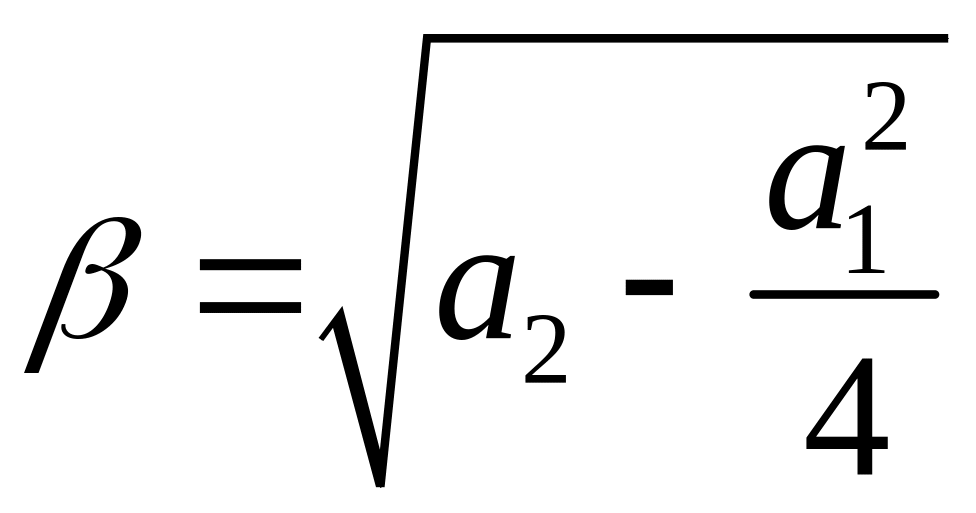 .
.
Частные решения можно записать в форме
![]() ,
,
![]() . (4)
. (4)
Это комплексные ф-ии действительного переменного х, удовлетворяющие дифф-му ур-ию (1).
Покажем, что комплексная функция действительного аргумента
![]() , (5)
, (5)
удовлетворяет ур-ию (1), то этому ур-ию удовлетворяют ф-ии u(x) и v(x).
Подставим ф-ию (5) в ур-ие (1)
![]() ;
;
![]() .
.
Комплексная ф-ия
равна 0, когда её действительная часть
-
![]() и мнимая часть -
и мнимая часть -
![]() равны 0,
равны 0,
т.е. ![]() ;
;
![]() .
.
След-но ф-ии u(x) и v(x) являются решениями ур-ия (1)
Решения (4) представим в виде суммы действительной и мнимой части:
![]() ,
,
![]()
По доказанным выше решениям
ур-ия (1) будит:
![]() ,
,
![]() . (6)
. (6)
Ф-ии
![]() и
и
![]() :
:
 ,
,
линейно не зависимы.
Общее решение ур-ия (1) будет:
![]() ,
,
или:
![]() ,
,
где С1, С2 – произвольные постоянные.
Примеры:
1) ![]()
![]()
Характеристическое
ур-ие:
![]() ;
;
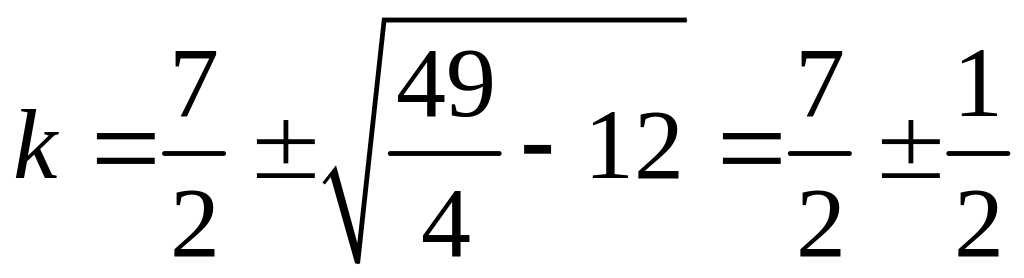 ; k1=3;
k2=4.
; k1=3;
k2=4.
![]() ; Общ.
решение
; Общ.
решение
![]() .
.
2) ![]() ;
;
![]() ;
; 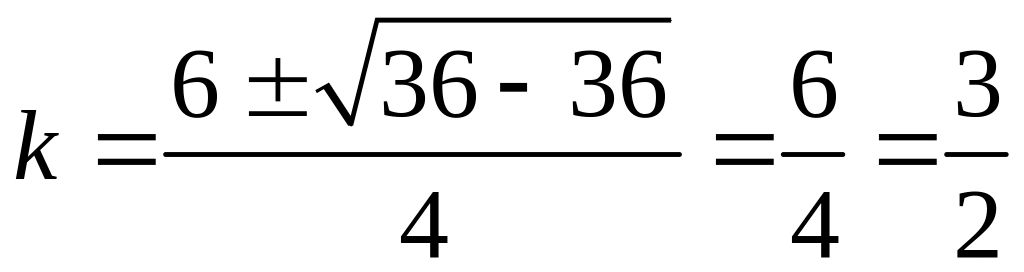 ;
;
![]() ;
;
Общее решение
![]() .
.
3) ![]() ;
;
![]() ;
; ![]()
Корни комплексные:
![]() ,
,
![]()
Общее решение
![]() .
.
§9 Линейные однородные уравнения n-го порядка с постоянными коэффициентами.
Линейное однородное ур-ие n-го порядка имеет вид:
![]() , (1)
, (1)
где а1, а2, …, аn – постоянные.
Определение: Если для всех x из отр. [a,b] имеет место равенство:
![]() ,
,
где А1,
А2,
…, Аn-1
– постоянные числа, не все равны нулю,
то говорят, что
![]() выражается
линейно через ф-ии
выражается
линейно через ф-ии
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Определение: n ф-ий , , …, называется линейно независимыми, если ни какая из этих ф-ий линейно не выражается через остальные.
Примеры. Определить будут линейно зависимыми или линейно независимыми ф-ии:
1) ![]() ,
,
![]() ,
,
![]()
![]()
при С1=3,
С2=0 ![]()
Ф-ии линейно зависимы
2) y1=1, y2=x, y3=x2 – линейно независимы.
![]() ;
;
![]() ; Нет
таких значений С1,
С2,
С3,
(не все одновременно равны нулю), чтобы
выполнялось это равенство.
; Нет
таких значений С1,
С2,
С3,
(не все одновременно равны нулю), чтобы
выполнялось это равенство.
Теорема: Если ф-ии y1, y2, …, yn являются линейно независимыми решениями ур-ия (1), то его общее решение есть:
![]() , (2)
, (2)
где С1, С2, …, Сn – произвольные постоянные.
Если в ур-ии (1) коэфф. постоянны, то общее решение находится также как и в случае ур-ия второго порядка.
Составляем характеристическое ур-ие:
![]()
Находим корни характеристического ур-ия k1, k2, k3, …, kn.
По характеру корней выписываем частные линейно не зависимые решения.
Найдя n линейно не зависимых частных решений y1, y2, …, yn, записываем общее решение.
![]() Примеры.
Примеры.
1)
![]()
Характеристическое уравнение
![]() ,
биквадратное уравнение
,
биквадратное уравнение
![]() =
=![]()
![]() 0
0
![]()

![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
Корни характеристического ур-ия действительные и различные
Общее
решение
![]()
2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Корни характеристического ур-ия действительные, разные и равные.
Общее
решение
![]()
10. Неоднородные линейные уравнения второго порядка.
10.1) Имеем неоднородное линейное уравнение второго порядка.
![]() (1)
(1)
Структура общего решения уравнения (1) определяется следующей теоремой.
Теорема
1 Общее решение неоднородного уравнения
(1) представляется как сумма какого-нибудь
частного решения этого уравнения
![]() и общего решения
и общего решения
![]() соответствующего однородного уравнения
соответствующего однородного уравнения
![]() (2)
(2)
Док-во. Нужно доказать, что сумма
![]() (3)
(3)
есть общее решение уравнения (1)
Подставим
сумму
![]() в уравнение (1)
в уравнение (1)
вместо
у , получим
![]() или
или
![]() (4)
(4)
т.к.
- решение уравнения (2), то
![]() =0
=0
-
частное решение уравнения (1), то
![]()
Равенство (4) представляет тождество
0 +
![]() =
=
Следовательно
![]() есть решение уравнения (1)
есть решение уравнения (1)
Докажем теперь, что выражение (3) есть общее решение уравнения (1), т.е. докажем , что входящие в него произвольные постоянные можно подобрать так, чтобы удовлетворялись начальные условия :
![]() ,
,
![]() (5)
(5)
каковы
бы ни были числа
![]()
Т.к.
![]() , где
, где
![]() -
линейно независимые решения уравнения
(2)
-
линейно независимые решения уравнения
(2)
![]() -
произвольные постоянные , то равенство
(3) примет вид
-
произвольные постоянные , то равенство
(3) примет вид
![]() (3’)
(3’)
Используя начальные условия (5) будем иметь
![]()
![]()
Мы получим систему уравнений для определения :
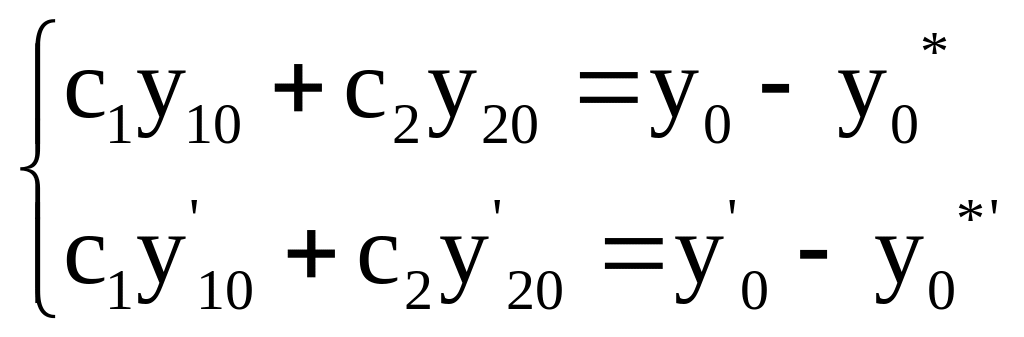 (6)
(6)
Система
(6) имеет решение, если

Этот определитель есть определитель Вронского
![]()
Т.к. функции линейно независимы, то
![]() ,
,
Следовательно система (6) имеет решение, т.е. существует такие значения , при которых формула (3) определяет решение уравнения (1), удовлетворяющего начальным условиям . Теорема доказана.
При отыскании частных решений полезно пользовться результатами следующей теоремы.
Теорема 2 Решение уравнения
![]() ,
(7)
,
(7)
где
правая часть есть сумма двух функций
![]() и
и
![]() ,
можно представить в виде суммы
,
можно представить в виде суммы
![]() ,
где
,
где
![]() и
и
![]() - соответственно решения уравнений
- соответственно решения уравнений
![]() (8)
(8)
![]() (9)
(9)
Док-во т.к. - решение уравнения (8), то
![]() ,
(10)
,
(10)
- решение уравнения (9) , то
![]() (11)
(11)
Складывая почленно (10) и (11) получим
![]()
Из последнего равенства следует, что сумма
![]()
есть решение уравнения (7)
Укажем общий метод нахождения частных решений неоднородного уравнения.
Метод вариации произвольных постоянных.
Имеем
![]() (1)
(1)
соотв.
лин. одн. ур-ия
![]() (2)
(2)
его
общее решение
![]() (3)
(3)
Будем искать частное реш. неодн. Ур-ия
(1) в форме (3) где
![]() и
и
![]() -
неизв. ф-ии от
-
неизв. ф-ии от
![]()
продифф (3)
![]()
подберем
и
так,
чтобы
![]() (4)
(4)
тогда
![]()
Дифференцируя
последнее, найдем
![]()
![]()
подставим
![]() ,
,
![]() ,
в ур-ии (1) получим
,
в ур-ии (1) получим
![]()
или
![]()
т.к.
![]()
![]()
то
![]() (5)
(5)
Итак ф-ия (3) будет решением неоднородного линейного ур-ия (1), если и удовлетворяют системе уравнений (4) и (5), т.е.
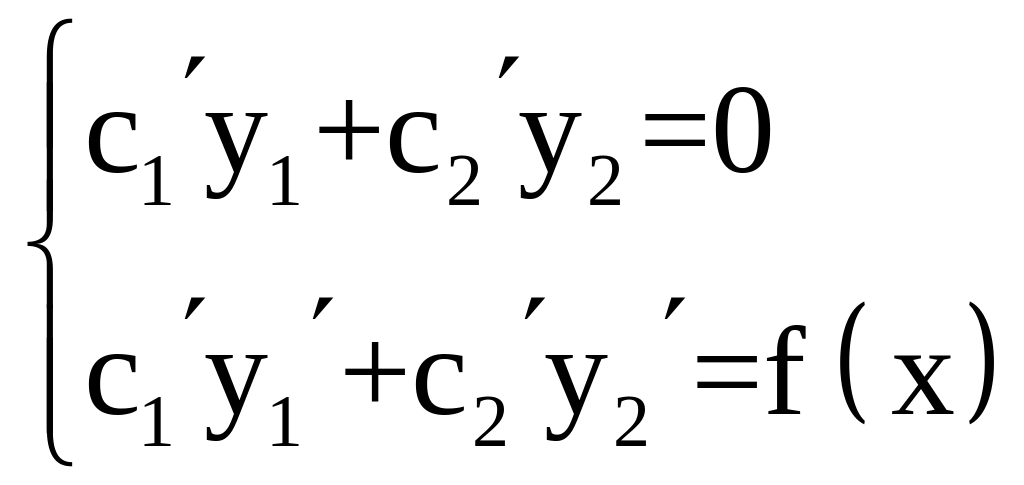
эта сист. имеет реш, т.к.
Определим
![]() и
и
![]() интегрируя, получим
интегрируя, получим
![]()
![]()
представляя в равенство (3) получим общее решение ур-ия (1).
Пример