Глава 7 периодические несинусоидальные токи в линейных электрических цепях

7.1. Причины отклонения переменных токов

От синусоидальной формы

Во многих практических случаях токи и напряжения в электрических цепях отличаются от синусоидальной формы. Причины отклонения токов от синусоидальной формы могут быть различные. Например, в радиотехнике, связи, вычислительной технике и т.д. используют импульсы различной формы (рис. 7.1,а, б), получаемые с помощью специальных устройств – импульсных генераторов. Простейший принцип получения прямоугольных импульсов с помощью периодического замыкания и размыкания ключа К показан на рис. 7.1,в.

Н

Рис 7.1 в)

а рис. 7.1,г показано последовательное соединение двух синусоидальных источников различной частоты: и . Выходное напряжение имеет несинусоидальную форму (рис. 7.1,е). При этом, если менять соотношения амплитуд, фаз и частоты источников, то соответственно будет изменяться каждый раз форма выходного напряжения.

Наличие нелинейных элементов также искажает синусоидальную форму сигналов. Пусть вольт-амперная характеристика нелинейного элемента . Тогда при воздействии на цепь синусоидального напряжения ток в цепи будет содержать первую и третью грамоники .

Различные формы сигналов используются в электронных устройствах. Так, для передачи сообщений по линиям связи осуществляют модуляцию гармонического сигнала по амплитуде (АМ), частоте (ЧМ), фазе (ФМ) или передаваемые импульсные сигналы, модулируют по амплитуде (АИМ), ширине (ШИМ), временному положению (ВИМ). Такие сигналы имеют сложную негармоническую форму. Электрические генераторы промышленной частоты генерируют э.д.с., строго говоря, несинусоидальной формы, так как зависимость индукции от напряженности поля, нелинейная. Кроме того, на форму э.д.с. влияют наличие пазов и зубцов, размещение обмоток и т. д. В силовой энергетике искажение формы напряжений и токов является вредным, так как увеличиваются потери в устройствах, например за счет гистерезиса и вихревых токов, и тем самым ухудшаются экономические показатели устройства.

7.2. Представление периодических несинусоидальных токов в виде рядов Фурье

Для анализа явлений, происходящих в линейных электрических цепях при воздействии несинусоидальных э.д.с. используют представление воздействий в виде сумм синусоидальных э.д.с. различной частоты. Другими словами, периодические колебания , удовлетворяющие условиям Дирихле (т.е. имеющие конечное число разрывов первого рода и конечное число максимумов и минимумов) могут быть представлены в виде ряда Фурье. Заметим, что колебания, используемые в элнктротехнических устройствах, всегда удовлетворяют условиям Дирихле. Периодическая функция f(t) может быть представлена в виде тригонометрического ряда Фурье:

,

(7.1)

где k – номер (порядок) гармоники; , – амплитуда и начальная фаза k-й гармоники; – постоянная составляющая или нулевая гармоника. Здесь и далее индекс в скобках (k) будет обозначать номер гармоники. Если k =1, гармоника называется основной (первой). При k =2, 3,…, n составляющие ряда носят название высших гармоник, период которых равен .

Используя соотношение

и, вводя обозначения: , ,  t=, записываем ряд (7.1) в виде:

.

(7.2)

Коэффициенты разложения определяем из выражений:

;	(7.3)
;	(7.4)
.	(7.5)

Как видно из (7.5), постоянная составляющая равна среднему значению функции f (t) за период основной гармоники . Иногда в рядах (7.1) и (7.2) постоянную составляющую обозначают , тогда (7.5) перепишется в виде

.

Коэффициенты и начальные фазы ряда (7.1) связаны с коэффициентами ряда (7.2) соотношениями:

.

(7.6)

При определении начальной фазы следует учитывать, в каком квадранте находится .

Разложение в ряд Фурье (7.2) различных периодических функций имеется во многих справочниках по математике. Для облегчения разложения следует учитывать свойства периодических функций. В табл. 7.1 показана связь условий симметрии периодической функции с содержанием гармонического ряда. Наличие коэффициентов разложения помечено знаком (+), отсутствие – знаком (0).

Разложение в ряд Фурье также зависит от выбора начала отсчета времени. При смещении начала отсчета изменяются начальные фазы и зависящие от них коэффициенты и , однако амплитуды гармоник и их взаимное расположение сохраняются.

Таблица 7.1

№ п.п.	Симметрия относительно	Коэффициенты ряда
		A(0)	Bm(k)	Cm(k)
1	Оси ординат	+ или 0	0	+
2	Начала координат	0	+	0
3	Оси абсцисс	0	+ только нечетные	+ только нечетные
4	Случаи 1 и 3 одновременно	0	0	+ только нечетные
5	Случаи 2 и 3 одновременно	0	+ только нечетные	0

При графическом изображении отдельных гармоник следует иметь ввиду, что масштабы углов по оси абсцисс для разных гармоник различ ны. Для k–й гармоники масштаб углов в k раз больше, чем для пер вой гармоники.Соответственно период k–й гармоники (угол ) занимает

Рис. 7.2

отрезок, в k раз меньший, чем для первой гармоники. Проиллюстрируем это на примере.

Пример 7.1

На рис. 7.2,а изображена несинусоидальная функция тока i, которая представлена суммой первой i₍₁₎ и третьей i₍₃₎ гармоник. Пользуясь шкалами, указанными на осях, требуется записать аналитическое выражение тока .

Решение

На рис. 7.2,б показан порядок вычисления начальных фаз гармоник. С учетом найденных по рис. 7.2,б амплитуд и фаз гармоник исходная функция будет записана в виде

Необходимо заметить, что для увеличения точности расчетов следует учитывать возможно большее количество членов ряда Фурье. Так как искомую функцию представить в виде бесконечного ряда Фурье невозможно, то ограничиваются понятием "практически точное" разложение, например, когда действующее значение всех высших гармоник не превышает 1% от действующего значения основной гармоники. Понятие "практически точное" разложение вводится не только для сокращения объема расчетов. Как уже отмечалось в главе 1 (часть I) схема замещения электротехнического устройства зависит от диапазона частот. Поэтому, увеличивая точность расчетов, мы все равно выйдем за рамки рассматриваемой модели электротехнического устройства. Следует также учесть, что функции, имеющие разрывы (скачки), при представлении их тригонометрическим рядом делают скачок вблизи разрыва, примерно на 18% больший, чем исходная функция (явление Гиббса).

Пример 7.2

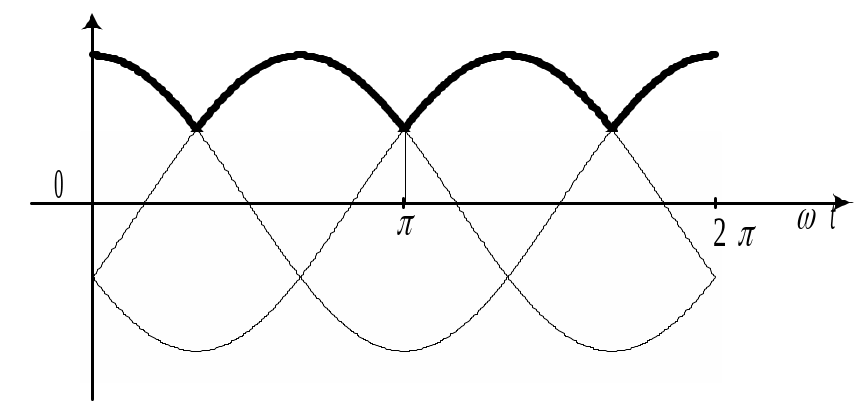
Рассмотрим разложение в ряд Фурье кривой выпрямленного напряжения (жирная линия) для случая m-фазного выпрямления, когда период функции в m раз меньше периода синусоиды питающего напряжения (рис. 7.3,а).

Решение

В этом специфическом случае номера гармоник k кратны числу фаз m и ряд Фурье содержит гармоники порядка k =n m, где n=1, 2, 3, 4,…, то есть k =m, 2m, 3m, 4m и так далее.

Определим коэффициенты ряда:

;			(7.7)
а)
б)		в)
Рис. 7.3

, где k=m, 2m, 3m, 4m….

(7.8)

Таким образом, разложение в ряд Фурье имеет вид

.

(7.9)

В частном случае двухполупериодного выпрямления m=2 (рис. 7.3,б) разложение в ряд Фурье имеет вид

.

(7.10)

Для трехфазного выпрямления m=3 (рис. 7.3,в) разложение (7.9) имеет вид

.

(7.11)

Представление функций в виде ряда (7.1) или (7.2) не всегда удобно. Например, при символическом методе расчета предпочтительнее использовать разложение в ряд Фурье в комплексной форме. При такой форме разложения также упрощаются операции интегрирования и дифференцирования.