§ 2.7.3. Классификация маршрутов.

Обобщённое представление всех описанных типов маршрутов на графах можно изобразить в виде условного графа.

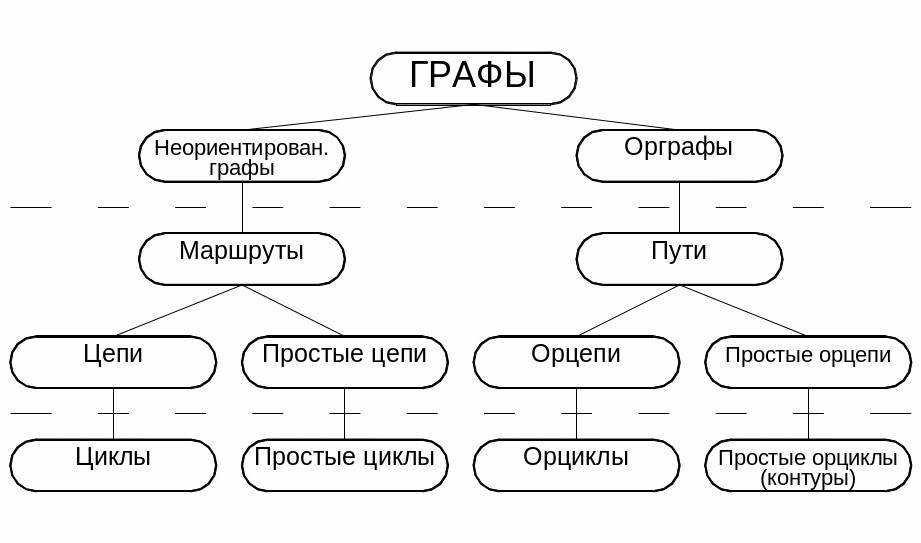
Эйлеровы циклы Гамильтоновы контуры

§ 2.8. Степени связности графов

Орграф называется сильно связанным или сильным, если для любых двух его различных вершин x_i и x_j существует по крайней мере один путь, соединяющий x_i и x_j

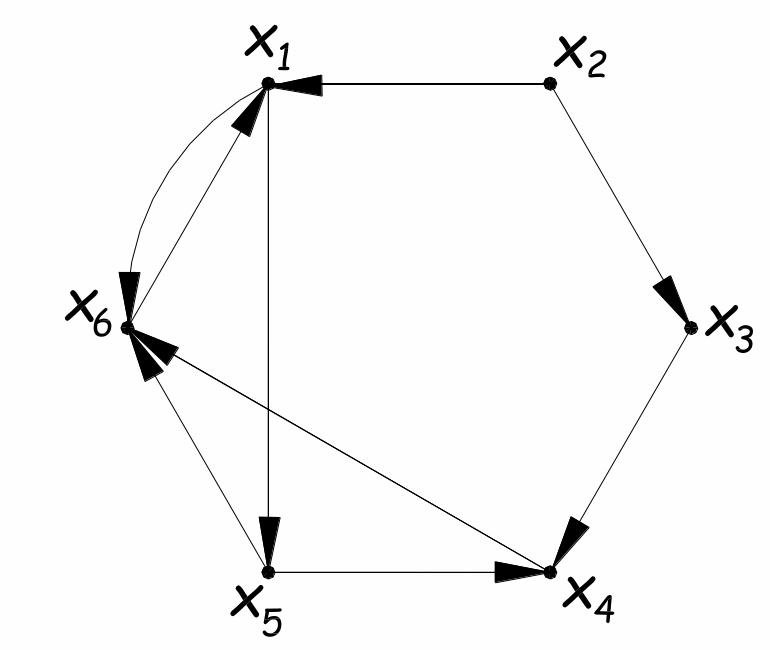
Орграф называется односторонне связанным или односторонним, если для любых двух его различных вершин x_i и x_j существует по крайней мере один путь: из x_i в x_j или из x_j в x_i (или оба).

Орграф называется слабо связанным или слабым, если для любых двух его различных вершин x_i и x_j существует по крайней мере один маршрут, соединяющий x_i и x_j .

Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой орграф называется несвязанным.

§ 2.8. Достижимость и связность.

Систему связи любой организации можно интерпретировать как граф, в котором люди представлены вершинами, а каналы связи – дугами.

Вопрос: может ли информация от одного лица x_i быть передана другому лицу x_j, т.е. существует ли путь, ведущий от вершины x_i к x_j?

Вершина х_j достижима из х_i , если в графе существует путь из х_i в х_j. Можно интересоваться достижимостью вершины x_j из вершины x_i на путях, длины которых не превосходят заданной величины.

На языке графов, представляющих организации, полезно рассматривать такие вопросы:

1. Каково наименьшее число сотрудников, для которых все другие сотрудники достижимы?

2. Каково наибольшее число сотрудников, которые взаимно достижимы?

§ 2.8.1. Матрицы достижимостей и контрдостижимостей. Существенные вершины

Пусть дан орграф G = (X,A).

Его матрица достижимостей R = [r_ij] определяется следующим образом:

r_ij = 1, если вершина x_j достижима из x_i

r_ij = 0, если вершина x_j недостижима из x_i

причём x_i, x_j  Х

Множество вершин R(x_i) графа G, достижимых из заданной вершины x_i, состоит из таких элементов x_j, для которых (i,j) – ые элементы в матрице достижимостей равны 1.

Х  R(x_i) = { x_j |  ( x_i x_j) }

Очевидно, что все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима из себя самой с помощью пути длины 0.

Отметим, что Г(x_i) является множеством вершин x_j, достижимых из x_i с использованием путей длины 1, а Г²(x_i) – множество вершин, достижимых из x_i с использованием путей длины 2, и т.д.

Аналогично Г^р(x_i) – множество вершин, достижимых из x_i посредством путей длины р. Следовательно, множество вершин, достижимых из x_i, можно представить в виде

R(x_i) = {x_i} U Г(x_i) U Г²(x_i) U … U Г^р(x_i) (1)

Если число вершин графа конечно, то длина путей р, при котором множество R(x_i) вберет в себя все возможно достижимые вершины графа, тоже конечно, хоть и может быть достаточно большим. Число р меньше числа вершин в графе.

Множество R(x_i) может быть получено последовательным объединением множеств из соотношения (1) до тех пор, пока “текущее” множество не перестанет увеличиваться по размеру при очередной операции объединения.

Чтобы построить матрицу достижимостей, надо найти достижимые множества R(x_i) для всех x_i Є Х. Причём r_ij = 1, если x_i Є R(x_i) и r_ij = 0 в противном случае.

Матрицу контрдостижимостей Q = [q_ij] определяют т.о.:

q_ij = 1, если из x_j можно достичь x_i

q_ij = 0, если из x_j нельзя достичь x_i

Контродостижимым множеством Q (x_i) графа G является множество таких вершин x_j этого графа, из которых можно достичь вершины x_i. Аналогично построению достижимого множества на основе соотношения (1) можно сформировать множество:

Q(x_i) = {x_i}U Г^-1(x_i) U Г^-2(x_i) U … U Г^-p(x_i) (2)

Операции выполняются слева направо до тех пор, пока очередная операция объединения не перестанет изменять текущее множество Q (x_i).

Чтобы построить матрицу контрдостижимостей, надо найти контрдостижимые множества Q(x_i) для всех x_i Є Х. Причём q_ij = 1, если x_i Є Q(x_i) и q_ij = 0 в противном случае.

Из определения видно, что столбец x_i матрицы Q совпадает со строкой матрицы R, т.е. Q = R^t , где R^t – матрица, транспонированная к матрице достижимостей R.

Поскольку R(x_i) является множеством вершин, достижимых из x_i, а Q(x_j) – множество вершин, из которых можно достичь x_j, то R(x_i)  Q(x_j) – множество таких вершин, каждая из которых принадлежит по крайней мере одному пути, ведущему от x_i к x_j. Эти вершины называются существенными или необъемлемыми относительно вершин x_i и x_j.

Все остальные вершины x_k  R(x_i)  Q(x_j), называются несущественными или избыточными, т.к. их удаление не влияет на пути от x_i к x_j.