Классы точности средств измерения

Класс точности – есть обобщенная метрологическая характеристика средств измерения, определяемая предельными значениями допустимой погрешности. Пределы допустимых погрешностей средств измерений выражаются в форме абсолютной, относительной и приведенной погрешностей [10].

Если погрешность средств измерений носит чисто аддитивный характер, то класс точности задается предельным значением приведенной погрешности γ_пр.:

.

Если погрешность средств измерений носит чисто мультипликативный характер, то класс точности задается предельным значением относительной погрешности δ_пр.:

.

Как правило, таким образом, нормируют средства измерения высокой точности (цифровые мосты, компенсаторы для измерения ЭДС термопары) и класс точности обозначают отношением .

Постоянные коэффициенты c, d, p, q есть отвлеченные положительные числа, выбираемые из ряда m 10n , где m = 1, 1.5, 2, 2.5, 3, 4, 5, 6; n = 1, 0, –1, –2, –3, …

Случайные погрешности проявляются при многократных и равноточных измерениях, т.е. при измерениях, выполненных по одной и той же методике, средствами одинаковой точности и при переменных внешних условиях.

Примеры случайной погрешности (трение в опорах рамки измерительных приборов, тепловое воздействие на рамку, изменение сопротивлений соединительных проводов, плохой контакт, влияние магнитных полей, влияние петли гистерезиса и т.д.).

Задача оценки случайной погрешности – указать границы изменения погрешности результата измерений при повторных измерениях (доверительный интервал).

Аналитически случайная погрешность измерений описывается и оценивается с помощью аппарата теории вероятностей и математической статистики. При такой оценке обычно интересуются вероятностью (R) того, что погрешность результата измерений (D) находится в некотором заданном доверительном интервале распределения погрешностей (–D_Г1, D_Г1), где –D_Г1 и D_Г1 соответственно нижняя и верхняя границы интервала. Записывается данная вероятность как R(–D_Г1 £ D £ D_Г1) и из математики известно, что в общем случае 0 £ R £ 1.

Для определения значения вероятности R(–D_Г1 £ D £ D_Г1) необходимо знать закон r(D) распределения случайной погрешности D, называемый плотностью распределения вероятностей (плотностью вероятностей) случайной погрешности D. При известном законе распределения r(D) искомая вероятность определяется по формуле

.

Из физических представлений следует, что вероятность нахождения погрешности D на интервале всех возможных погрешностей измерений, т.е. в общем случае на интервале (–¥, +¥) равна .

Данное выражение называется условием нормирования плотности распределения вероятностей r(D), которое означает, что площадь под графиком любой функции r(D) на интервале всех ее значений должна быть равна единице.

В практике измерений наиболее часто используются нормальный (Гаусса) законы распределения погрешностей.

Нормальный закон распределения погрешностей

Для характеристики свойств случайной величины в теории вероятности используется понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии используют преим. Дифференциальную – закон распределения плотности вероятностей случайной величины.

Пусть произведено n=50 наблюдений величины x_i : x₁, x₂ x₃,….x_n,

Номер интервала	1	2	3	4	5
nk	5	10	18	11	6
nk/n	0,1	0,2	0,36	0,22	0,12

Н

n	xi
1	20
2	21
3	25
4	22
5	29
6	28
7	20
…	…
50	27

айдем размах ряда L = x_max, - x_{min = 29-19=10} Разделив размах ряда на k=5 равных интервалов l = L/k = 10/5=2, подсчитаем количество наблюдений n_k , попадающих в каждый интервал.

При бесконечном повторении и увеличении n ступенчатая кривая перейдет в плавную кривую f(x) – кривая плотности распределения вероятности случайной величины.(Или )

Числовые характеристики распределений:

1. Математическое ожидание (среднее арифметическое):

= 25

2. Среднее квадратичное отклонение (СКО) или рассеивание единичных результатов и дисперсияч:

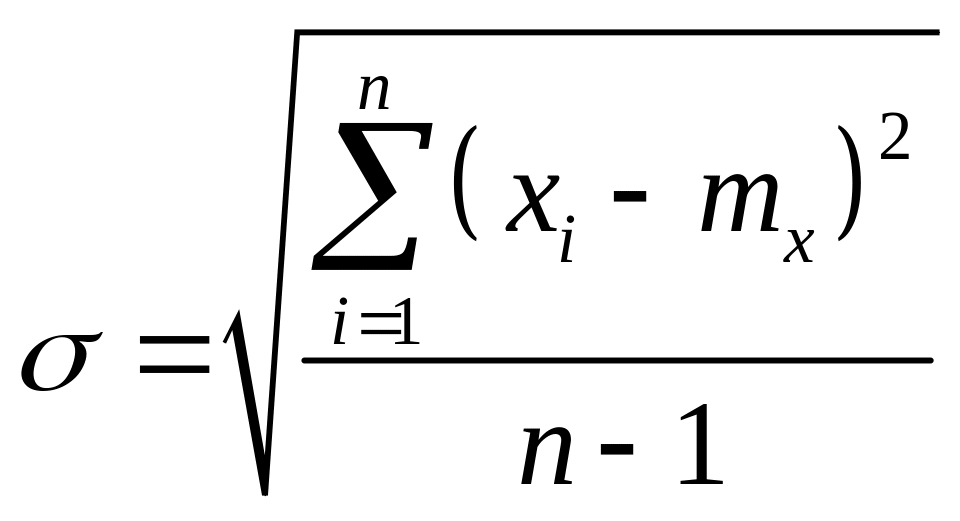D = s²,

где D – дисперсия.

Качество и точность измерений тем выше, чем меньше СКО, тем меньше вероятность рассеивания результатов наблюдений D.

Рис 1.12. Графики нормального закона распределения плотности вероятности случайных погрешностей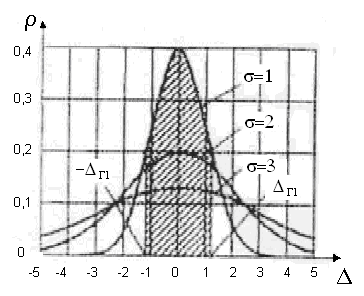

Чаще начало координат совмещают с центром распрелделения.

В аналитической форме закон нормального закона распределения записывают:

f(x)= .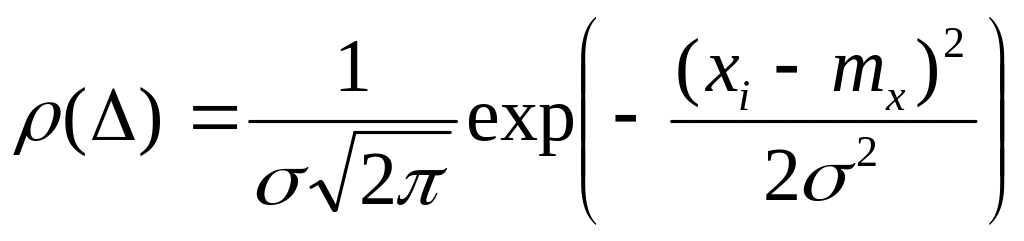

где s – среднеквадратическое отклонение (СКО), характеризующее точность выполненных измерений (чем меньше s, тем выше точность). По мере уменьшения s рассеяние случайных погрешностей D относительно центра их распределения, (в данном случае относительно значения D = 0) уменьшается. На рис. 1.12 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратичного отклонения. Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

На графике плотности вероятности для конкретного СКО (см. рис. 1.12) вероятность численно равна площади S заштрихованной фигуры, ограниченной функцией r(D), отрезком оси D от –D_Г1 до D_Г1 и ординатами r(–D_Г1), r(D_Г1). Чем шире заданный интервал погрешностей, тем больше площадь S, т.е. больше вероятность попадания случайных погрешностей измерений D в этот интервал. Для интервала (–¥,+¥) вероятность R(–¥ £ D £ +¥) =1.

Более универсальным методом является оценки погрешности с использованием доверительных интервалов: На графике норм. распределения отложены интервалы с границами ± ±2 и т.д.

Доверительные вероятности для этих интервалов в таб. В технике принят 99% уровень надежности, т.е. границы ±3.

t	P
±1	0,68
±2	0,95
±3	0,997
±4	0,999