
- •Устойчивость, порытия, паросочетания
- •1.1. Основные определения
- •1.2. Определение чисел ε0(g), π0(g), π1(g).
- •Алгоритм выделения пустых подграфов.
- •1.3. Определение чисел β0(g), β1(g).
- •1.5. Плотность p(g) графа g.
- •1.6. Максимальный поток через сеть.
- •Задачи для самостоятельного решения.
- •2. Раскраска вершин и ребер графа.
- •2.1. Понятие раскраски вершин и ребер графа
- •Раскраска вершин графа.
- •Оценки химического числа h(g).
- •2.3. Раскраска ребер графа.
- •2.4. Алгоритм минимальной раскраски вершин (ребер) графа g
- •Задачи для самостоятельного решения.
- •3. Планарность графа.
- •1.1. Основные определения……………………………………………...
- •Для студентов всех форм обучения специальностей «Компьютерные системы и сети», «Системное программирование»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ
УНИВЕРСИТЕТ
СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ «ДИСКРЕТНАЯ МАТЕМАТИКА»
(ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ, ЧАСТЬ ІІ)
Северодонецк СТИ 2001
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ
УНИВЕРСИТЕТ
СЕВЕРОДОНЕЦКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ «ДИСКРЕТНАЯ МАТЕМАТИКА»
(ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ, ЧАСТЬ ІІ)
для студентов всех форм обучения специальностей «Компьютерные системы и сети», «Системное программирование»
Северодонецк СТИ 2001
Методические указания к практически занятиям по курсу «Дискретная математика» (элементы теории графов, часть II) для студентов всех форм обучения специальностей «Компьютерные системы и сети», «Системное программирование» (Сост. А.Е. Богданов, - Северодонецк : СТИ, 2001 . – 49 с.
Составитель А.Е. Богданов
Данные методические указания содержат темы, не вошедшие в первую часть одноименных методических указаний.
Устойчивость, порытия, паросочетания
1.1. Основные определения
Множество вершин графа называется внутренне устойчивым, если они попарно не смежны.
Внутренне устойчивое множество вершин графа называется пустым подграфом, если при добавлении хотя бы одной вершины, не принадлежащей этому множеству, образуется хотя бы одно ребро (дуга).
Пример 1. В графе G (рис.1.1) выделить внутренне устойчивое множество вершин и пустой подграф.
1



2 6

5
4
G
Рис. 1.1
Внутренне
устойчивыми множествами вершин для
графа G
являются множества вершин![]() {1,3,5}
и
{1,3},
указанные на рис. 1,2 а, б. Внутренне
устойчивое множество вершин
{1,3,5}
является пустым подграфом, т.к. добавление
любой вершины графа G,
не вошедшей в множество
{1,3,5},
приводит
к образованию ребер. Например, добавление
вершины 4 приводит к образованию ребер
(3,4) и (4,5) (рис.1.2в). Внутренне устойчивое
множество вершин
{1,3}
не является пустым подграфом, т.к.
добавление вершины 5 не приводит к
образованию ребра (рис.1.2г).
{1,3,5}
и
{1,3},
указанные на рис. 1,2 а, б. Внутренне
устойчивое множество вершин
{1,3,5}
является пустым подграфом, т.к. добавление
любой вершины графа G,
не вошедшей в множество
{1,3,5},
приводит
к образованию ребер. Например, добавление
вершины 4 приводит к образованию ребер
(3,4) и (4,5) (рис.1.2в). Внутренне устойчивое
множество вершин
{1,3}
не является пустым подграфом, т.к.
добавление вершины 5 не приводит к
образованию ребра (рис.1.2г).
 1
1
1
1
m

3 5 3
а) б)
1
 3 5
3 5
3 4 5
в) г)
Рис. 1.2 ■
Максимальная мощность пустого подграфа графа G называется числом внутренней устойчивости или вершинным числом независимости ε0(G) графа G.
Максимальное число попарно несмежных ребер графа G называется реберным числом независимости ε1(G) графа G.
Если ребро инцидентно вершине, то говорят, что они покрывают друг друга. Множество вершин, покрывающих все ребра графа, называется покрытием графа G. Минимальная мощность вершинного покрытия π0(G) графа G.
Аналогично, множество ребер, покрывающих все вершины графа G, называются реберным покрытием графа. Минимальн6ая мощность реберного покрытия графа G называется числом реберного покрытия π1(G).
Условимся считать, что любая вершина графа покрывает сама себя и две смежные вершины покрывают друг друга. Тогда минимальная мощность множества вершин, покрывающих все вершины графа G, называется вершинным числом внешней устойчивости графа β0(G).
Аналогично будем считать что каждое ребро графа покрывает себя и два смежных ребра покрывают друг друга. Тогда минимальная мощность множества ребер, покрывающих все ребра графа G, называется реберным числом внешней устойчивости β1(G).
Теорема 1.1. Для любого нетривиального связного графа G = < V, U > ε0(G) + π0(G) = ε1(G) + π1(G) = |V| . (1.1)
Множество ребер графа, в котором низкая пара ребер не смежна, называется паросочетанием графа.
Множество ребер паросочетания, в котором число ребер равно ε1, называется наибольшим паросочетанием графа.
Теорема 1.2. Для двудольного графа G число ребер в наибольшем паросочетании равно числу вершинного покрытия, т.е. ε1 = π0.
Окрестностью G ( v0) вершины v0 графа G = < V, Г > называется подграф <V0, U0>, носитель которого совпадает с окрестностью единичного радиуса этой вершины, V0=Гv0,
а сигнатуру U0 образуют все ребра графа G, соединяющие вершины из V0.
Неокрестностью
![]() (v0)
вершины v0
графа G
= < V,
Г > называется подграф
(v0)
вершины v0
графа G
= < V,
Г > называется подграф
<V0,
U0>,
носитель которого V0
= {
vi
/ vi
![]() Гv0
}, сигнатура
U0
состоит из
всех ребер графа G,
соединяющих вершины из V0.
Гv0
}, сигнатура
U0
состоит из
всех ребер графа G,
соединяющих вершины из V0.
Пример 2. Указать G( v0) и ( v0) вершины v0 графа G, изображенного на рис. 1.3.
v9

 v8
v8
 v1
v7
v1
v7
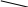
 v2
v2
 v3
v3
v6


 v0
v0
v4 v5
G
Рис. 1.3
С огласно
определению G(
v0)
= <V0,
U0>,
где V0=Гv0,
а U0
– ребрf
графа G,
соединяющие из вершины V0.
огласно
определению G(
v0)
= <V0,
U0>,
где V0=Гv0,
а U0
– ребрf
графа G,
соединяющие из вершины V0.
Значит, V0=Гv0= = { v1, v2 , v3, v4}, U0 = = { (v1, v2) , ( v2, v3), , ( v3, v4), }, (рис. 1.4а).
Согласно определению ( v0) = <V0, U0>, где V0 = { vi / vi Гv0 }, а U0 – ребрa графа G, соединяющие вершины из V0. Значит,
V0= { v5, v6 , v7, v8, v9 }, U0 = = { (v5, v6) , ( v7, v8), , ( v8, v9) } (рис. 1.4 б)
v1
 v2
v9
v2
v9

 v8
v8
 v3
(
v0)
v7
v3
(
v0)
v7
G( v0)
v6

v4
v5
а) б)
Рис. 1.4
