Додаток 3

Практичне заняття

Тема: Кільце. Підкільце.

Мета: Сформувати поняття кільця, підкільця, області цілісності, дослідити базові кільця, сформувати вміння знаходити дільники нуля та оборотні елементи, використовувати означення та ознаку підкільця.

Хід заняття

1. Запитання для повторення та актуалізації

Математичний диктант

1. Кільце – це… . Приклади.

2. Підкільцем називають … . Приклади.

3. Сформувати ознаку підкільця.

4. Який елемент називають дільником нуля?

5. Елемент називають оборотним до елемента 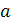, якщо…

6. Кільце називається кільцем з одиницею, якщо…

7. Яке кільце називають комутативним?

8. Що називають областю цілісності?

2. Завдання для аудиторної роботи.

Задача 1: Перевірити чи утворює задана множина кільце відносно операцій

додавання та множення.

.

Розв’язання:

Правило – орієнтир:

8. Перевірити чи задана множина є замкнена відносно традиційних операцій додавання та множення дійсних чисел;

9. Вибрати шлях доведення: за означенням чи за ознакою;

10. За означенням перевірити:

4. Чи є дана множина абелевою групою по додаванню, тобто перевірити:

А) чи є операція додавання асоціативною, комутативною;

Б) чи містить дана множина нульовий елемент;

В) визначити протилежний елемент для кожного елемента множини;

5. Чи є дана множина півгрупою по множенню, тобто чи є операція множення асоціативною;

6. Чи виконуються дистрибутивні закони;

11. За ознакою перевірити:

3. Чи є дана множина підмножиною множини відомого кільця;

4. Чи замкнена множина відносно додавання, віднімання та множення будь-яких двох елементів множини.

Добре відомими, з школи, прикладами алгебраїчних структур є такі числові множини з традиційними операціями додавання та множення:

- множина цілих чисел;

Q – множина раціональних чисел;

R – множина дійсних чисел.

Множини , Q, R утворюють абелеві групи відносно додавання. Числові множини , є абелевими групами відносно множення

Розв’язання проводимо за допомогою ознаки підкільця.

1. Дана множина є підкільцем кільця R.

2. Перевіримо замкненість множини відносно додавання:

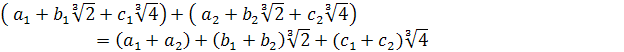
тобто, додавання даних чисел зводиться до додавання цілих чисел при відповідних показниках степеня числа 2. А отже, задана множина є замкненою відносно додавання. Так як, в множина цілих чисел є замкненою відносно віднімання, то і задана множина також є замкненою множиною відносно цієї операції.

3. Перевіримо замкненість множини відносно множення:

Отримане число є числом заданої множини. Отже, множина є замкненою відносно множення.

Таким чином, дана множина є кільцем відносно операцій додавання та множення.

Вправи на закріплення:

1. Перевірити, чи утворює множина 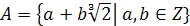відносно операцій додавання та множення кільце.

2. Довести, що множина 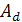комплексних чисел виду , d –фіксоване ціле число, що не ділиться на квадрат простого числа, x, y – цілі числа однакової парності.

(Вказівка: 1) відносно додавання розглянути такі випадки:

• всі числа 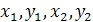однакової парності (або всі парні, або всі непарні)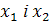

• різної парності (тобто )

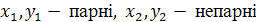2) для дослідження замкненості відносно множення необхідно припустити, що замкнена відносно множення, розглянути добуток таких чисел , .

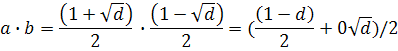
Оскільки елемент повинен належати до , то мусить бути парним числом, звідки випливає, що d дає остачу 1 при діленні на 4 (будемо записувати цей факт так: .

3) відносно множення розглянути три можливі випадки:

- – парні.

- парні.

- - непарні.)

3. Нехай М – множина, В(М) – множина всіх її підмножин. Доведіть, що 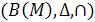є комутативним кільцем ( 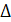- розглядається як додавання, 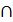- розглядається як множення).

Запитання для закріплення

1. Навести приклад множини, що не утворює кільце.

2. Чи утворює множина 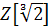- комутативне кільце? Кільце з одиницею?

Задача 2: Перевірити, чи є множина A підкільцем кільця .

Розв’язання: (за ознакою)

1. , тому що

2. , тому що

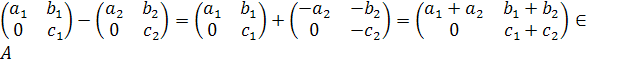3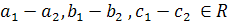. , тому що

Отже, А – підкільце .

Вправи на закріплення:

4. Перевірити, чи є множина А підкільцем .

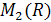А) ;

Б) ;

В)

Г) .

5. Довести, що підмножина кільця K з одиницею е утворює підкільце.

Запитання для закріплення:

1. В якому випадку доведення, що множина є підкільцем кільця K можна звести до двох кроків:

1. 

2. 

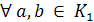
2. Навести приклад кільця R з одиницею 1 і його підкільця S, яке також є кільцем з одиницею е, причому .

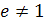Задача 3: Знайти оборотні елементи та дільники нуля у кільці

.

Розв’язання:

Правило – орієнтир:

1. Для того щоб знайти всі оборотні елементи потрібно знайти всі елементи для яких виконується умова .

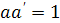2. Для того щоб знайти всі дільники нуля потрібно знайти всі ненульові елементи 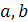для яких виконується умова .

1. 

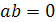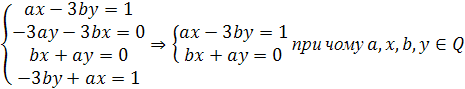
Отже, дільниками одиниці є всі ненульові матриці виду , при чому , , .

2)

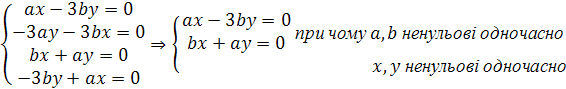
Якщо , то і , що суперечить означенню.

Якщо , не можлива ситуація для ненульових чисел.

Таким чином, в кільці К немає дільників нуля.

Вправи на закріплення:

6. Знайти оборотні елементи та дільники нуля у кільцях:

a) .

б)

в){ }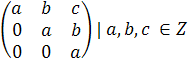

Запитання для закріплення:

1. Знайти всі оборотні елементи кільця . (Вказівка:

).

2. Довести, що в кільці з одиницею без дільників нуля, кожен елемент, котрий має односторонній обернений, є оборотним.

3. Описати дільники нуля та оборотні елементи у кільці .

4. Довести, що якщо кільця Rє дільником нуля, то і є дільниками нуля.

Завдання для самостійного опрацювання:

6. Довести, що А є кільцем, при чому А – адитивна абелева група, а операція множення визначена таким чином: .

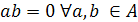7. Знайти оборотні елементи та дільники нуля у кільцях:

4. ;

8. Перевірити, які з кілець є кільцями з дільниками нуля. В даних кільцях знайти дільники одиниці та дільники нуля.

4. ,

;

5. ,

;

6. ,

.