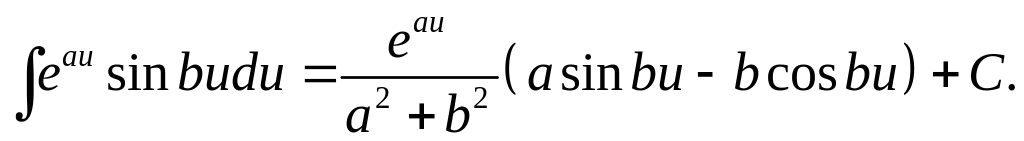Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Ярославский государственный технический университет»

Кафедра «Высшая математика»

Неопределенный интеграл

Методические указания

для студентов очного отделения

Ярославль 2009

УДК 517(07)

МУ 26-. Неопределенный интеграл указания / сост.: В.Ш. Ройтенберг, Л.А. Сидорова – 2-е изд., испр. и доп. – Ярославль : Изд-во ЯГТУ, 2009. – 33.

Содержат краткие теоретические сведения по разделу «Неопределенный интеграл», подробно разобранные типовые задачи, даны задачи для самостоятельного решения. Могут быть использованы студентами на практических занятиях и при выполнении домашних заданий.

Предназначены для студентов 1-го курса всех специальностей очного отделения.

Библиогр. 7

Рецензенты:

____________________________________________________________________

____________________________________________________________________

 Ярославский государственный технический университет, 2009

1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ТАБЛИЦА ОСНОВНЫХ

НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

1. Сведения из теории

1. Определение первообразной и неопределенного интеграла

Функция F(x) называется первообразной функции на промежутке J, если . Любая непрерывная функция , , имеет первообразную. Множество всех первообразных функции , , называется неопределенным интегралом от этой функции и обозначается . Пусть какая-нибудь первообразная функции , , тогда

,

где C – произвольная постоянная.

2. Свойства неопределенного интеграла

1. .

2. .

Это равенство означает, что неопределенный интеграл от функции состоит из первообразных функции , умноженных на число a.

3. .

Это равенство означает, что неопределенный интеграл от суммы состоит из всевозможных сумм первообразных функций и .

3. Задача интегрирования элементарных функций

Как известно, производная от элементарной функции является элементарной функцией и существует алгоритм ее нахождения. Для обратной операции интегрирования – ситуация иная. Первообразная элементарной функции может быть и неэлементарной функцией. Из неэлементарных функций состоят, например, важные для приложений интегралы

от «простых» на вид функций (отметим, что неэлементарность этих функций не помешала изучить их не хуже, чем, скажем, синус).

Тем ни менее, существует ряд приемов, позволяющих выразить некоторые интегралы в виде элементарных функций. Эти приемы основаны на преобразовании интегралов к интегралам из таблицы основных неопределенных интегралов, полученной «обращением» таблицы производных.

4. Таблица основных неопределенных интегралов

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

1. Примеры решения задач

   1. Убедиться, что функция является первообразной функции на .

◄ Действительно, при любом

. ►

2. Убедиться, пользуясь определением, что .

◄ Так как , то

. ►

3. Вычислить .

◄ При вычислении этого интеграла применим свойства 2, 3 и табличный интеграл 1.

. ►

4. Вычислить .

◄ При вычислении этого интеграла применим тождественные преобразования (возведение суммы в квадрат и деление суммы на число), свойства 2, 3 и табличные интегралы 1 и 2.

. ►

5. Вычислить .

◄ При вычислении этого интеграла применим тождественные преобразования, свойство 2 и табличный интеграл 10

= .►

6. Вычислить .

◄ При вычислении интеграла применим тождественные преобразования, свойство 2 и табличный интеграл 11

. ►

7. Вычислить .

◄ При вычислении применяем тождественные преобразования, свойство 2 и табличный интеграл 9.

. ►