Лабораторна робота №2

Тема: Алгебраїчний метод розв’язання ЗЛП: симплекс-метод

Мета роботи: Вивчити алгебраїчний метод розв’язання задач лінійного програмування.

Ключеві слова: канонічна форма моделі ЗЛП, опорний план, симплекс-таблиця, розрішаюций стовпець (строка), розрішаючий елемент, симплексні перетворення

Теоретичні відомості

Одним з універсальних методів рішення задач лінійного програмування є симплексний метод, називаний також методом послідовного поліпшення плану.

Нехай задача записана в канонічній формі:

(1)

(2)

(3)

Якщо задачу (1)-(3) можна розв'язати, то її оптимальне рішення збігається принаймні з одним з опорних рішень (планів) системи рівнянь (2). Саме цей результат і покладений в основу побудови симплекс-методу. У його обчислювальній схемі реалізується упорядкований процес, при якому, починаючи з деякого вихідного припустимого плану, здійснюються послідовні переходи від однієї припустимої екстремальної точки до іншої доти, доки не буде знайдена точка, що відповідає оптимальному рішенню. Упорядкованість розуміється в тім змісті, що при переході від одного опорного плану до іншого відповідні їм значення цільової функції (1) зростають. Так як число опорних планів скінченне, то через кінцеве число кроків або буде знайдений оптимальний план, або встановлена нерозв'язність задачі.

При ручному розрахунку результати обчислень зручно оформляти у виді симплекс-таблиці (див. табл. 1)

Таблиця 1.

Сбаз.	Хбаз	А0	c1	c2	…	ci	…	cn	, >0
			Х1	Х2	…	Хi	…	Хn
		А10	а11	а12	…	а1i	…	а1n
…	…	…	…	…	…	…	…	…	…
		аk0	аk1	аk2	…	аki	…	аkn
…	…	…	…	…	…	…	…	…	…
		аm0	аm1	аm2	…	аmi	…	аmn
		z			…		…

Симплекс-алгоритм складається з наступних кроків:

1. приводимо задачу до канонічного виду;

2. знаходимо вихідне опорне рішення;

3. складаємо симплекс-таблицю;

4. обчислюємо оцінки 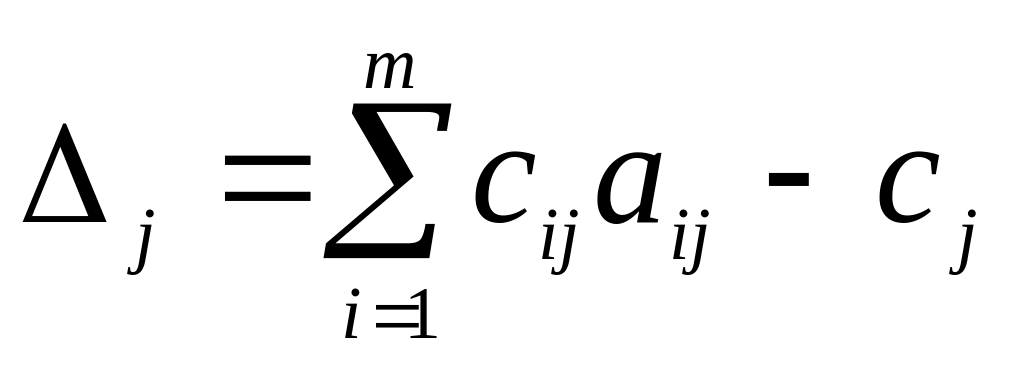для кожного j= :

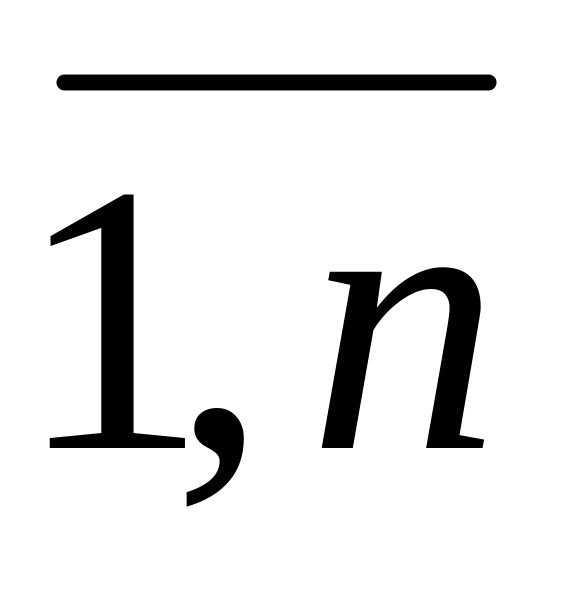• якщо всі оцінки 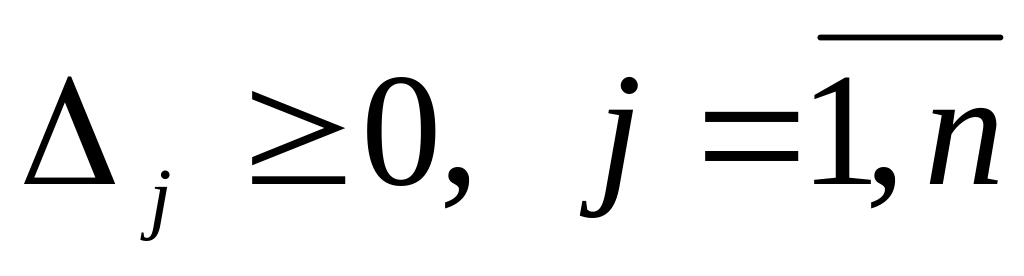то знайдене рішення оптимальне;

• якщо серед оцінок j є від’ємні, і знайдеться стовпець, що не містить додатних елементів, то функція z необмежена в ОДР (z )

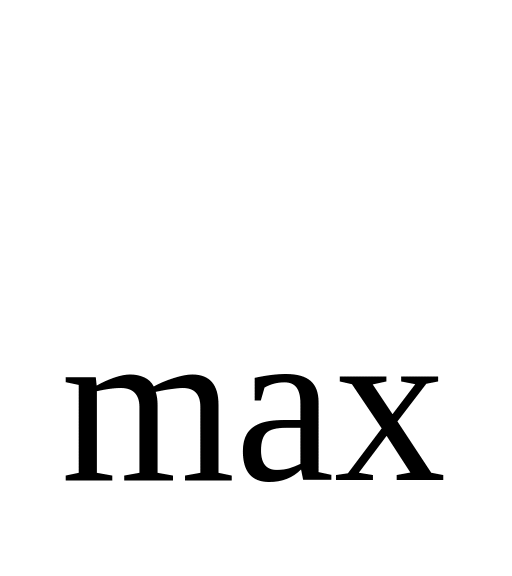• якщо серед оцінок j є від’ємні й у кожнім стовпці з такою оцінкою буде хоча б один додатних елемент, то виконуємо ще одну ітерацію.

5. знаходимо направляючий стовпець і направляючий рядок:

• стовпець визначається найбільшим по модулі від’ємним числом j ;

• рядок визначається мінімальним з відношень 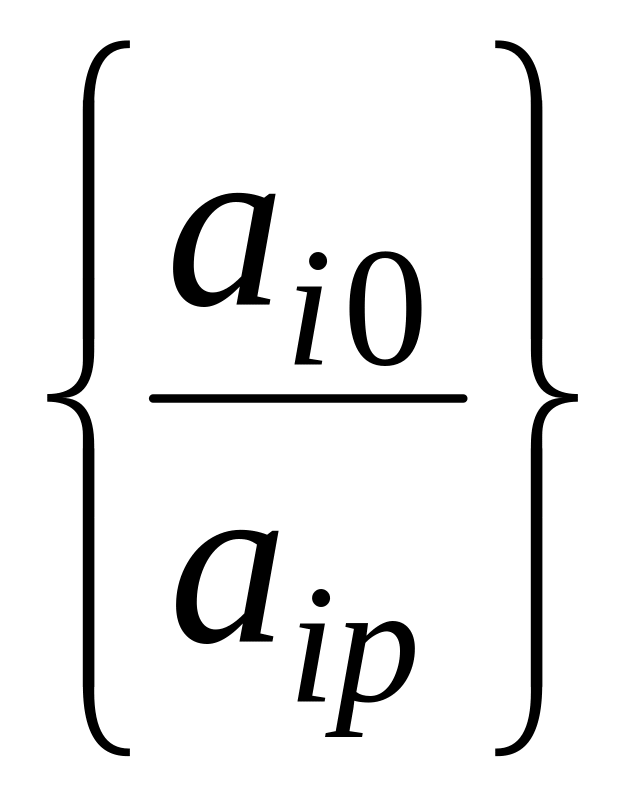, >0;

6. виконуємо симплексні перетворення з вибраним розрішаючим елементом:

7. переходимо до кроку 4.

Приклад. Вирішити наступну ЗЛП симплекс-методом

Рішення. Приведемо задану модель до канонічної форми, вводячи додаткові змінні та ,що перетрорюють обмеження- нерівності в рівності:

.

Початкове опорне рішення визначається базисом Х₃, Х₄ та має вигляд Х=(0, 0, 2, 6).

Побудуємо симплекс-таблицю (таблиця 2) та занесемо в неї вихідні данні

Таблиця 2

Сбаз.	хбаз.	Аі0	3	2	0	0	, >0
			Х1	Х2	Х3	Х4
0	Х3	2	1	-1	1	0	1
0	Х4	6	2	1	0	1	3
		0	-3	-2	0	0

Елементи строки обчислені за формулами:

Так як серед оцінок є від’ємні, то знаходимо розрішаючий стовпець, та розрішаючу строку. Розрішаючим стовпцем буде Х₁ , так як він має максимальну по модулю від’ємну оцінку =-3.

Розрішаючу строку визначаємо склавши відношення , >0, та визначивши з них мінімальне. Так як , то розрішаючою строкою буде перша строка. Отже, розрішаючим єлементом буде . Зоповнюємо нову симплекс-таблицю (таблиця 3), що відповідає новому опорному рішенню, використовуючи правила переразрахунків метода Жордана-Гауса.

Таблиця 3

Сбаз.	хбаз.	Аі0	3	2	0	0	, >0
			Х1	Х2	Х3	Х4
3	Х1	2	1	-1	1	0	-
0	Х4	6	0	3	-2	1	2
		6	0	-5	3	0

Оскільки в стрічці оцінок є від’ємні переходимо до наступної ітераціі, продовжуючи поліпшувати опорний план. Розрішаючим єлементом вибираємо , так як він є єдиним додатнім єлементом в стовпці з від’ємною оцінкою. Результати наступних ітерацій приведені в таблицях 4, 5.

Таблиця 4

Сбаз.	хбаз.	Аі0	3	2	0	0	, >0
			Х1	Х2	Х3	Х4
3	Х1	2	1	0			8
2	Х2		0	1			-
		6	0	0

Таблиця 5

Сбаз.	хбаз.	Аі0	3	2	0	0	, >0
			Х1	Х2	Х3	Х4
0	Х2	8	3	0	1	1
2	Х3	6	2	1	0	1
		12	1	0	0	2

Так як всі , то план, представлений в таблиці 5 буде оптимальним. Відповідь. Х_опт=(0, 8, 6, 0), Z_max=12.

Часні випадки рішень злп

1. Виродженість.

Визначення 1: Опорне рішення, у якому хоча б одна з базисних змінних приймає нульове значення, називається виродженим, а ЗЛП, що має хоча б одне вироджене рішення – виродженою задачею.

Наявність виродженого рішення з практичної точки зору порозумівається наявністю в моделі принаймні одного надлишкового обмеження.

Ознакою появи виродженого рішення при розрахунках в симплекс таблиці є наявність кілька рівних мінімальних відносин , тобто ми можемо вибрати розрішаючий елемент неоднозначно.

У випадку виродженої ЗЛП ми можемо зіштовхнутися з зацикленням, тобто після декількох ітерацій можна повернутися до базису, що раніше зустрічався. Щоб цього уникнути у виборі розрішаючого рядка потрібно користатися додатковим правилом: якщо виявляється кілька рівних мінімальних відносин , то варто вибирати той рядок, для якого буде найменшим відношення елементів наступного стовпця до розрішаючого .

2. Альтернативні оптимальні рішення.

Коли пряма чи площина (гіперплощина), що представляє цільову функцію, рівнобіжна прямій чи площині (гіперплощини), що відповідає зв’язуючому обмеженню (яке в точці оптимуму виконується як точна рівність), цільова функція приймає одне і теж оптимальне значення в деякій сукупності точок простору рішень. Такі рішення називаються альтернативними оптимальними рішеннями. Звичайно існує нескінченна безліч альтернативних рішень.

Ознакою існування альтернативного рішення при розрахунку симплексними таблицями є наявність хоча б однієї нульової оцінки вільної змінної при невід’ємності всіх інших оцінок.

Якщо X₁, X₂,…,X_S оптимальні рішення задачі, то загальне рішення буде

Якщо маємо 2 оптимальних рішення, то загальне рішення запишеться у виді

, де t[0, 1].

Інформація про наявність альтернативних оптимумів виявляється корисною при рішенні практичних задач, тому що вид, що приймає рішення, дає можливість вибору альтернативного варіанта, найбільшою мірою відповідного сформованій ситуації, і при цьому немає необхідності досліджувати зміни цільової функції.

3. Необмежені рішення.

Умови деяких ЗЛП можуть допускати нескінченне збільшення значення змінних без порушення накладених обмежень, отже цільова функція може нескінченно зростати. У такому випадку говорять, що простір рішень, і оптимальне значення цільової функції необмежені.

Необмеженість рішення ЗЛП говорить про те, що: 1) у моделі не враховано одне (чи декілька) обмеження, що не є надлишковим; 2) неточно оцінені параметри, що фігурують у деяких задачах.

Загальне правило для виявлення необмеженості: якщо на деякій ітерації небазисна змінна має в обмеженнях від’ємні (0) коефіцієнти у всьому стовпці, то простір рішень необмежено в цьому напрямку. Якщо, крім того коефіцієнт j<0 при цій змінний, то в цьому випадку і цільова функція також необмежена.

4. Відсутність припустимих рішень.

Якщо обмеження моделі одночасно виконуватися не могуть, то задача не має припустимих рішень. Таке рішення завжди існує, коли всі обмеження моделі типу (мається на увазі незаперечність правих частин обмежень), оскільки введення залишкових змінних завжди забезпечує одержання деякого припустимого рішення. Однак, якщо модель містить обмеження інших типів, звичайно використовуються штучні змінні, не гарантуючі одержання припустимого рішення задачі в її первісній постановці.

З практичної точки зору відсутність припустимих рішень варто розглядати як свідчення того, що модель побудована некоректно, тому що введені обмеження виявилися суперечливими. Можливо також, що ці обмеження насправді і не повинні виконуватися одночасно. У цьому випадку необхідно побудувати модель, що має зовсім іншу структуру і не припускає одночасного невиконання всіх обмежень.