1. Равномерное распределение

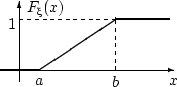
Пример! Точка бросается на интервал вещественной прямой (a;b)

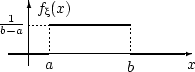
Такую случайную величину называют равномерно распределенной на интервале (a,b) и обозначают

Математическое ожидание и дисперсия: ,

2. Показательное распределение.

параметр распределения.

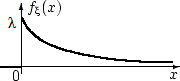
В случайные моменты времени происходит некоторое событие. Такая ситуация называется поток событий.

Поток событий называется Пуассоновским с интенсивностью λ, если вероятность что за время t произойдет m событий, вычисляется: , λ – среднее число успехов(событий) за единицу времени.

Пусть T – случайная величина – это время между двумя последними наступлениями событий. Т – функция распределения:

t>0.

Показательное распределение можно считать распределением времени безотказной работы какого-то устройства, если отказы распределены по пуассоновскому закону.

- функция надежности устройства.

Математическое ожидание и дисперсия: ,

3. Нормальное распределение.

С.в. называется нормальным распределением, если 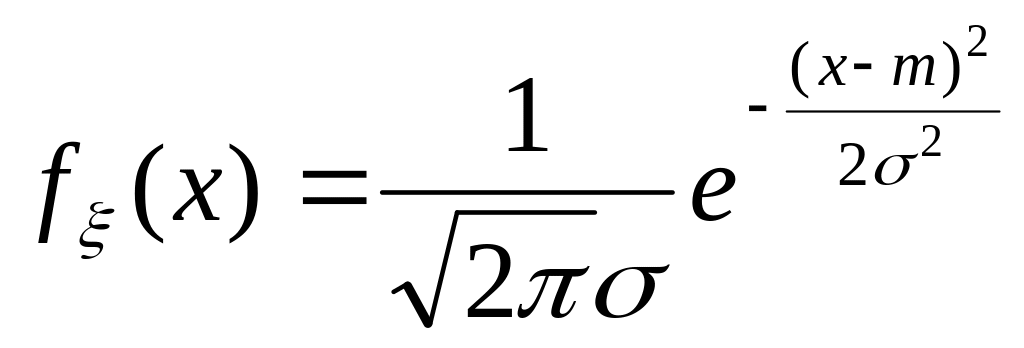, m, σ – параметры распределения, , .

- стандартное нормальное распределение.

(ξ имеет нормальное распределение с параметрами m, σ), N – Нормальное

Нормальному или приближенно-нормальному распределению св-ся ограниченное число реальных процессов происходящих в природе.

Нормальная величина попадает в интервал (a;b)

Математическое ожидание и дисперсия: , .

Заключение: Не надо думать что все случайные величины являются либо дискретными либо непрерывными, большинство не относится к чисто дискретным или непрерывным, такие величины называются смешанными или сингулярными.

Основные дискретные распределения:

1)Гипергеометрическое распределение.

,

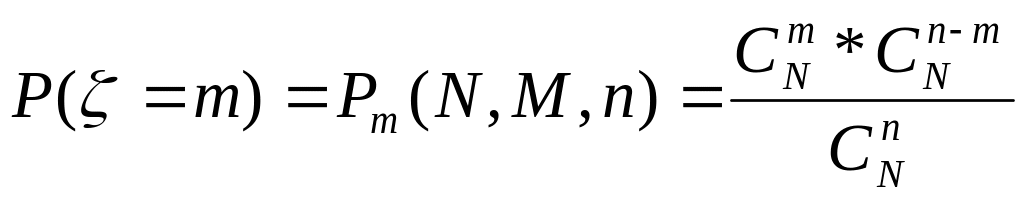m- целое неотрицательное число, N – количество шаров, M – количество белых, n – вытащили, в m это количество белых.

2) Биномиальное распределение или распределение Бернулли.

, m=0,1,…,n

имеет биномиальное распределение с параметрами n и p, n- число независимых испытаний, p – число успехов.

Математическое ожидание и дисперсия: , .

3) Распределение Пуассона

Математическое ожидание и дисперсия: , .

4) Геометрическое распределение

Пусть проводятся независимые испытания Бернулли с вероятностью p успехов в каждом испытании, с.в. ζ есть номер испытания в котором произошел первый успех.

.

Математическое ожидание и дисперсия: , .

3. Закон больших чисел, центральная предельная теорема.

Под ЗБЧ понимается совокупность утверждений о том, что средние случайных величин при большом их числе ведут себя почти как не случайные.

Неравенство Чебышёва.

ξ(кси) – случайная величина, - т.е. конечное число, тогда , . Вероятность уклонения случайной величины от своего мат. ожидания.

Теорема Чебышёва.(ЗБЧ)

Пусть - последовательность независимых случайных величин, имеющих равномерно ограниченную дисперсию тогда , .

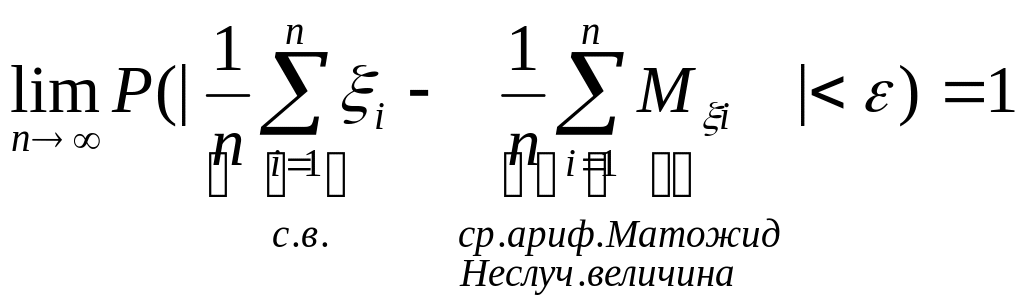Доказательство:

- среднее арифметическое.

,

Переходя к пределам получаем требуемое в теореме.

Опр. Последовательность сходится по вероятности к случайной величине ξ, если

( по вероятности р стремится к ξ).

ЗБЧ тогда говорит: средние случайных величин по вероятности сходятся к среднему мат. ожиданий.

ЗБЧ в виде теоремы Бернулли.

- число успехов в последовательности n независимых испытаний с вероятностью p

, .

вероятность в отдельном испытании.

Опр. сходится к с.в. ξ почти наверное (п.н.) если

Если последовательность сходится п.н., то она сходится и по вероятности. Обратное в общем неверно.

Характеристические функции.

- комплексная с.в.

Все свойства переносятся.

Опр. ξ –с.в. Характеристической функцией , .

ξ- дискретная с.в.

тогда .

Если ξ – непрерывная с плотностью , то .

Центральная предельная теорема.

ЦПТ – это совокупность утверждений о том, что суммы с.в. при большом количестве слагаемых ведут себя чаще всего как нормальные случайные величины.

Теорема

Пусть - одинаково распределенные и независимые случайные величины с и и тогда случайная величина 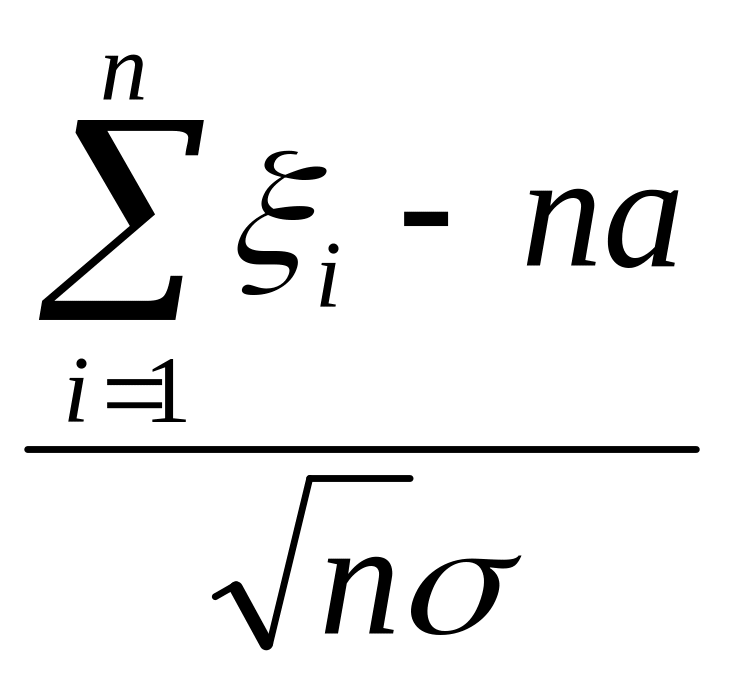по распределению сходится к стандартной нормальной величине. Вычитая и деля мы фактически центрируем и нормируем и поэтому в результате мы получаем нормальное распределение. .

Доказательство:

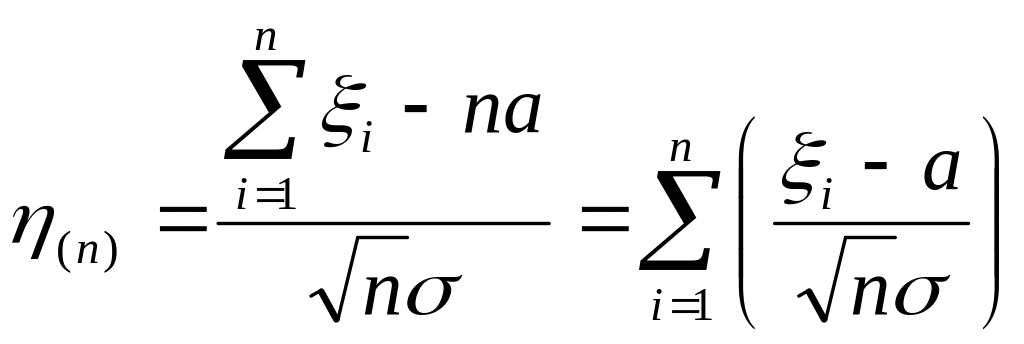
Пусть - характеристическая функция величины .

по теореме о разл. харакеричстических функций (до 2-го порядка), т.к. существует конечная дисперсия.

или , тогда .

Отсюда последовательность функции распределения стремится к функции распределения, более того сходимость равномерная.