Операторы импульса и энергии

Продифференцируем -функцию по :

Или

Таким образом, значение импульса мы получим как множитель перед -функцией, если применить к ней операцию ‑ . Эту операцию будем называть оператором импульса ‑ . Таким образом

Аналогично можно получить и для других координат:

Найдем теперь выражение для оператора энергии из условия, что должно выполняться равенство . Для этого продифференцируем -функцию по времени:

Отсюда

Т.е. оператор энергии имеет вид:

Уравнение Шредингера

С другой стороны, энергия частицы имеет вид: , где ‑ кинетическая энергия, ‑ потенциальная энергия. Т.е.

Квадрат импульса равен сумме квадратов проекций импульса, т.е.

Представим теперь проекции импульсов в виде операторов:

Т.е.

Аналогично и по другим координатам:

Следовательно, оператор кинетической энергии будет иметь вид:

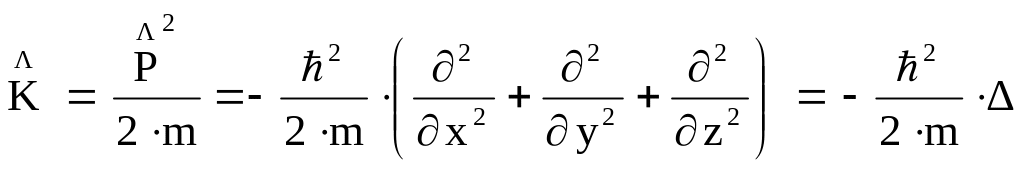
где ‑ оператор Лапласа ‑ .

Таким образом, оператор кинетической энергии будет иметь вид:

Потенциальная энергия содержит только координаты. Поэтому оператор есть просто умножение на функцию .

Таким образом, оператор полной энергии, называемый оператором Гамильтона , будет иметь вид:

Таким образом, используя предыдущее выражение для оператора полной энергии, мы получим следующее уравнение:

(6)

Это уравнение называется уравнением Шредингера. В раскрытом виде уравнение Шредингера имеет вид:

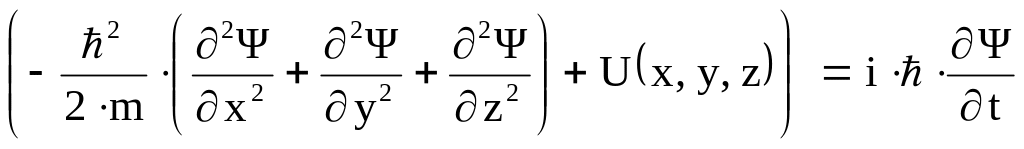(7)

Уравнение Шредингера для стационарных состояний имеет вид:

(8)

Специальными исследованиями было показано, что это уравнение при больших массах переходит в уравнение классической физики.

Пример

Р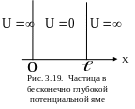 ассмотрим заряженную частицу в бесконечно глубокой, одномерной потенциальной яме (см. рис. 3.19).

Поскольку случай одномерный и стационарный, то уравнение Шредингера будет иметь вид:

Вне потенциальной ямы -функция будет равна нулю.

Внутри потенциальной ямы , и поэтому для этой области пространства уравнение Шредингера будет иметь вид:

Граничные условия для функции записываются как:

Преобразуем уравнение для :

Введем обозначение:

Окончательное дифференциальное уравнение для нахождения -функции будет иметь вид:

Как видим, получили дифференциальное уравнение незатухающих колебаний (I.2.4), только не во времени, а в пространстве. Решение этого уравнения имеет вид (I.2.6):

Константы интегрирования и находятся из граничных условий.

1. Удовлетворим граничному условию в нуле ‑ . Получим ‑ . Отсюда вытекает, что константа интегрирования . Таким образом, -функция будет иметь вид ‑ .

2. Удовлетворим теперь второму граничному условию ‑ . Получим ‑ . Отсюда вытекает, что должно выполняться условие ‑ , где Таким образом, для циклической частоты колебаний в пространстве получаем следующее выражение:

Следовательно, -функции будет иметь вид:

Выражение для амплитуды -функции найдем из условия нормировки ‑ . Для нашей задачи условие нормировки будет иметь вид:

Возьмем интеграл этого уравнения:

Следовательно, условие нормировки примет вид:

Окончательно -функцию представим в виде:

Г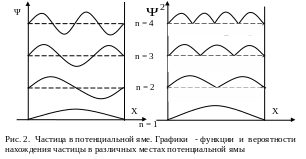 рафики самой -функции и ‑ характеризующий вероятность нахождения частицы в том или ином месте потенциальной ямы, представлены на рис. 2.

Получим теперь выражение для энергии частицы в потенциальной яме.

Из выражения для квадрата частоты следует, что . Из граничных условий вытекает, что . Объединяя эти два условия, получим:

Мы видим, что энергия частицы квантуется, принимает дискретный ряд значений.