И к w2 , если

Такая процедура минимизирует ожидаемую стоимость ошибочной классификации

q₁C(2|1)Pr(2|1)+q₂ C(1|2)Pr(1|2).

Для обобщенной байесовской процедуры вероятности ошибочной классификации имеют вид

и

где

Решение системы (1) можно записать в матричных обозначениях

a = e^-1( m₁-m₂ ) ,

где a = ( a₁ , ... , a_p )^T.

Расстояние Махалонобиса

D2 = ( m₁-m₂ ) ^T e-1( m₁-m₂ ) .

Классификация в случае двух многомерных нормальных групп при неизвестных параметрах

Пусть имеется объект , которому соответствует вектор наблюдений X. Требуется отнести его на основе этих наблюдений к группе W1 с распределением

или к W2 :

Предполагается , что известны априорные информации и стоимости ошибочной классификации , но средние m₁ и m₂ и матрица ковариаций e неизвестны. Если

x₁₁, ... , x_1n1 и x₂₁ , ... , x_2n2 - независимые случайные выборки из групп W1 , ... , W2 соответственно , то можно оценить m_i выборочным вектором средних x~=( x_i1 , ... , x_ip )^T,

i=1,2 , а e - объединенной выборочной ковариационной матрицей S = ( s_jk ) , где j,k=1,...,p.

В такой ситуации невозможно найти процедуру классификации, которая была бы оптимальной в смысле стоимости ошибочной классификации. Однако можно показать, что если параметры в обобщенной байесовской процедуре заменить их состоятельными оценками , то в результате ожидаемая стоимость ошибочной классификации будет убывать при n₁ и n₂ стремящихся к бесконечности. Поскольку приведенные выше оценки состоятельны, обобщенная процедура байесовской классификации на основе оценок параметров заключается в следующем :

1) решается система уравнений (1) с заменой m_ij на x~_ij i=1,2 , j=1,...,p, и заменой s _jm на s_jm,

m=1,...,p.

2) полученные оценки коэффициентов a ₁ ,..., a _p ( обозначим их через a ₁ , ... , a _p ) используется для определения значения дискриминантной функции z_il для каждого вектора наблюдений X_il , l = 1,..,n _i . Далее, z _i оцениваются величинами

а s_z² _{- величиной}

Таким образом, обобщенная байесовская процедура оценивания состоит в отнесении

X=( x₁ , ... , x_p )^T к W1 , если

и к W2 - в обратном случае.

Выборочное расстояние Махалонобиса

является оценкой для D² .

В результате работы программ дискриминантного анализа, как правило получаем следующее:

1) оценки коэффициентов дискриминантной функции a ₁ , ... , a _p ;

2) значение дискриминантной функции z_il для каждого вектора наблюдений X_il , i=1,2 ,

l=1,.., n _i

3) выборочные средние z~₁ и z~₂

4) выборочное расстояние Махалонобиса D ² .

Эта информация достаточна для классификации.

Замечания.

1) В результате работы программ дискриминантного анализа обычно выводится значение F-статистики

которое можно использовать для проверки гипотезы H₀ : D² = 0. Числа степеней свободы F равны p и n ₁ + n ₂ - p - 1

2) Выборочная оценка D ² расстояния Махалонобиса является смещенной. Несмещенная оценка имеет вид

Классификация в случае k групп с произвольными известными распределениями.

Пусть f _i (X) означает плотность распределения X в Wi и q _i - априорную вероятность того, что вектор наблюдения X принадлежит группе Wi, i = 1 , ... , k . Обозначим стоимость отнесения наблюдений Wj к Wi через C( i | j ), а вероятность отнесения наблюдения из Wj к Wi - через Pr( i | j ), i,j = 1 , ... , k , i<>j. Полагая, что все параметры известны, можно показать, что обобщенная байесовская процедура классификации относит вектор X к Wi, если величина

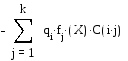i # j

является максимальной, i = 1 , ... , k. (Если одинаковый максимум достигается как в i ₁ , так и в i ₂ , то X относится к Wi ₁ или Wi ₂ ). Эта величина называется значением дискриминантной функции для i-й группы. Байесовская процедура минимизирует ожидаемую стоимость ошибочной классификации

i # j

Когда стоимость ошибочной классификации не имеет значения, все C( i | j ) полагаются равными и процедура Байеса относит X к Wi, если

q _i f _i (X) (4)

имеет максимальное значение, i = 1 , ... , k. Таким образом, минимизируется ожидаемая вероятность ошибочной классификации

i # j

Заметим, что это эквивалентно отнесению X к Wi, если апостериорная вероятность

достигает максимума.

Классификация в случае групп с многомерными нормальными распределениями.

Пусть группа Wi имеет распределение

с функцией плотности f _i (X) , i = 1 , ... , k. Будем считать, что все параметры известны и стоимости ошибочных классификаций равны. Подставляя f _i (X) в (4) , логарифмируя и исключая общие множители, получаем линейную дискриминантную функцию для i-й группы

d_i = a_i1 * x₁ + ... + a_ip * x_p + g_i *ln q_i , i = 1 , ... , k. (5)

Итак, вектор наблюдений X относится к группе Wi, если значение d_i является максимальным среди всех i = 1 , ... , k. Апостериорная вероятность принимает вид

Предположение о том, что параметры распределений известны облегчает только теоретическую часть анализа. На практике, как правило, имеются независимые случайные выборки из k групп по которым можно получить оценки параметров. При этом не существует оптимальной процедуры классификации, но подстановкой состоятельных оценок в выражение (5) можно получить асимптотическую оптимальную процедуру.

Пусть n _i - объем i-й выборки, x~_i - ее вектор средних и S_i - ковариационная матрица,

i = 1 , ... , k. Тогда в формуле (5) можно заменить m_i на x~_i и e - на объединенную ковариационную матрицу S :

Таким образом, оценка дискриминантной функции для i-й группы имеет вид

d_i = a_i1 * x₁ + ... + a_ip * x_p + c_i +ln q_i , i = 1 , ... , k.

Вектор X классифицируется, как принадлежащий группе Wi, если величина d_i имеет наибольшее значение. При этом оценка апостериорной вероятности имеет вид

Резюме. Программы дискриминантного анализа предназначаются, как правило, для вычисления следующих величин :

1) объединенной матрицы ковариации S и ковариационных матриц S_i для группы Wi,

i = 1 , ... , k ;

2) оценок для коэффициентов линейной дискриминантной функции a_i1 , ... , a_ip и постоянной c_i для группы Wi, i = 1 , ... , k ;

3) оценок значения линейной дискриминантной функции для каждого элемента x_im выборки из Wi, m = 1 , ... , n , i = 1 , ... , k ;

4) оценки апостериорной вероятности для каждой группы Wj при заданном векторе x_im , который является m-м элементом выборки из Wi , m = 1 , ... , n_i , i , j = 1 , ... , k ;

5) номеров групп, к которым относится векторы - элементы выборки из Wi, m = 1 , ... , n_i ,

i = 1 , ... , k ( тех групп для которых оценка апостериорной вероятности для дискриминантной функции достигает наибольшего значения ).

6) таблицы результатов классификации n_ij векторов x_jm выборки из Wj отнесенных к Wi

m = 1 , ... , n_j , j = 1 , ... , k . С помощью этой таблицы можно оценить вероятность ошибочной классификации Pr^( i | j ) = n_ij / n_j , i , j = 1 , ... , k , i<>j.

7) обобщенного расстояния Махалонобиса V - обобщение величины D² . Оно может быть использовано для проверки гипотезы H₀ : m₁ = ... = m_k . Заметим, что проверка гипотезы H₀ : m₁ = ... = m_k является многомерным аналогом однофакторного дисперсионного анализа. Многие программы выводят на печать так называемую U-статистику, которая является точной для проверки гипотезы H₀ . В виду сложности распределения величины U на печать выводится ее F-аппроксимация и соответствующее число степеней свободы. Такой критерий является точным для p = 1,2 при любых k или же при k = 2 для любых p.