Санкт-Петербургский Государственный

Электротехнический Университет «лэти» Факультет Компьютерных Технологий и Информатики отчет

ПО ПЕДАГОГИЧЕСКОЙ ПРАКТИКЕ

Тема Лекции: Рандомизированный алгоритм построения выпуклой

оболочки

Лекция по курсу: Вычислительной геометрии (комбинаторные алгоритмы).

Направление: 510200 – Прикладная математика и информатика

Специализация: 510209 – Математическое и программное обеспечение вычислительных машин

Студент гр. 0382: Сорокин А.Е.

Санкт-Петербург

- 2006 –

РАНДОМИЗИРОВАННЫЕ АЛГОРИТМЫ В ЗАДАЧАХ ВЫЧИСЛИТЕЛЬНОЙ

Геометрии

1. Рандомизированная пошаговая конструкция как основной подход к созданию рандомизированных алгоритмов вычислительной геометрии

Один довольно простой подход к созданию рандомизированных геометрических алгоритмов дает использование рандомизированной пошаговой конструкции . Здесь п объектов, составляющих входные данные к задаче, рассматриваются по одному в каждый момент времени в произвольном порядке, и вычисляется результат воздействия на решение каждого добавленного объекта. Для многих геометрических задач этот подход похож на многие известные алгоритмы, за исключением того, что в них обычно объекты обрабатываются в порядке, существующем на входе, а не в произвольном порядке.

Перед переходом к конкретным геометрическим задачам, рассмотрим простой негеометрический алгоритм, который поясняет использование рандомизированной пошаговой конструкции - рандомизированную пошаговую сортировку. Дано n чисел, которые нужно отсортировать. Используется следующая схема для их сортировки. После i-ого из п шагов (1 < i < n) имеем i вставленных чисел в отсортированный список. Ясно, что эти i отсортированных чисел разобьют ранги (n-i) еще не отсортированных чисел на (i+1) интервалов. (i+1)-ый шаг состоит в выборе одного из (n-i) еще не отсортированных чисел случайным образом и вставки его в отсортированный список. После п таких шагов вставки мы получаем отсортированный список входных чисел.

Рассмотрим подробно этот шаг вставки. По ходу алгоритма мы будем хранить указатель на каждое число до тех пор, пока оно не будет вставлено в отсортированный список. После i-ого шага указатель для каждого не вставленного числа определяет в какой из (i+1) интервалов в отсортированном списке оно должно быть вставлено, если бы оно было следующим, которое бы вставлялось. Указатели двунаправлены, так что если дан интервал, мы можем определить числа, указатели которых указывают на него. Какая работа требуется, чтобы сохранить эти указатели? Предположим, что мы вставляем число х, указатель которого указывает на интервал I. При вставке х, мы имеем три задачи: (1) найти все числа, указатели которых указывают на I; (2) обновить указатели всех чисел, чьи указатели указывают на I; (3) удалить указатель от х к I. Рассмотрим задачу (2). Задача обновления состоит в изменении каждого из указателей так, чтобы указать его на один из двух новых подинтервалов I, образованных вставкой х. Ясно, что работа, проведенная на этом шаге обновления, пропорциональна числу указателей, указывающих на I.

Рассмотрим работу, проделанную на i-ом шаге, когда объекты на входе рассматриваются в случайном порядке. Воспользуемся обратным анализом, т.е. представим, что алгоритм выполняется назад, начиная с того, что уже имеется отсортированный список. Таким образом, при анализе i-ого шага прямого алгоритма мы представляем, что мы удаляем одно из i чисел в отсортированном списке и обновляем указатели. Видно, что работа по обновлению указателей в этом случае такая же, как если бы алгоритм выполнялся вперед как обычно. Ключевым моментом в обратном анализе является следующий: так как в первоначальном алгоритме числа были добавлены в произвольном порядке, то в обратном анализе мы можем принять, что каждое число в отсортированном списке равновероятно может быть удалено на этом шаге. Каково ожидаемое число указателей, которые должны быть обновлены на этом шаге? Так как у нас i интервалов и (n-i+1) указателей, оставшихся после удаления, ожидаемое число указателей, которые были изменены на i-ом шаге - О((п-i)/i), которое есть О(п/i). Теперь мы используем линейность математического ожидания, чтобы просуммировать проделанную работу по всем шагам и получить верхнюю границу математического ожидания полной работы. Так как

где у - константа Эйлера, получаем 0() = О(п 1оg п).

Описанный подход открывает путь к дальнейшему изучению рандомизированных пошаговых алгоритмов для множества геометрических задач.

Рандомизированный алгоритм построения выпуклой оболочки

Обозначим выпуклую оболочку множества точек S через conv(S). Граница conv(S) образует выпуклый многоугольник, вершины которого - подмножество S. Всякий раз, когда нет опасности путаницы, мы будем относиться к этому многоугольнику как к conv(S). Задача вычисления выпуклой оболочки на плоскости состоит в следующем: дано S, требуется вычислить многоугольник (ограничивающий) conv(S). Результат должен быть представлен в виде списка, содержащего точки S, которые являются вершинами conv(S), перечисленные в порядке против часовой стрелки по их появлению в многоугольнике; начальная точка для списка может быть произвольной. Для определенности, будем считать, что первая точка в этом упорядочении - точка из S, имеющая наименьшую х - координату. Для простоты предполагаем, что в S нет трех точек, лежащих на одной прямой. При реализации от этого предположения можно отказаться.

Покажем, как рандомизированная пошаговая конструкция, описанная выше (в разделе 1.) в контексте сортировки, может применяться к этой задаче.

Алгоритм сначала случайным образом переставляет точки во входном множестве S. Пусть p_i- i-ая точка в этом случайном упорядочении (1 ≤ i ≤ п). Пусть S_i,- - набор {p₁, ..., p_i,}.

Затем алгоритм продолжается на п шагах. После i-ого шага, алгоритм вычислит conv(S_i). На i-ом шаге к conv(S_i-1) добавляется p_i, формируя conv(S_i). Теперь определим подробности этого шага модификации.

Пусть мы всегда храним точку во внутренней области conv(S); в частности мы могли бы использовать для этой цели центр масс conv(S₃) (который может быть вычислен за постоянное время). Обозначим эту точку p₀. Также после i-ого шага мы имеем список, содержащий вершины conv(S_i). Кроме того, для простоты описания, мы полагаем, что этот список также содержит ребра, соединяющие последующие вершины в этом списке (этого можно легко избежать в реализации с незначительной дополнительной работой). Пусть S\S_i, - множество точек, которые должны быть добавлены после i-ого шага, 3 ≤ i ≤ (п-1). Для каждой точки , мы сохраняем (двунаправленный) указатель от р на сторону conv(S_i), пересекаемую лучом, который исходит из р₀ и проходит через р. Мы будем говорить, что р пересекает данное ребро conv(S_i). Таким образом, если дано любое ребро conv(S_i), мы можем перечислить все точки р, которые пересекают это ребро во времени, линейно зависящем от числа таких точек.

Определив структуры данных, опишем действия, которые требуются для обновления этих структур на каждом шаге. Точка p_i, вставленная на i-ом шаге, находится или внутри, или вне conv(S_i-1). Используя отрезок р_i р₀ и связанный указатель, мы всегда можем определить положение р_i (наше допущение, что никакие три точки не являются коллинеарными, препятствует возможности нахождения р_i на границе conv(S_i-1)). Если р_i находится внутри conv(S_i-1), мы удаляем указатель от р_i и переходим к шагу (i+1). Иначе, если р_i находится вне conv(S_i-1), мы должны обновить список, представляющий собой многоугольник, ограничивающий оболочку. Вершины conv(S_i-1) разделяются на три множества при добавлении р_i:

1. Вершины conv(S_i-1), которые должны быть удалены, потому что они не вершины .

2. Две вершины conv(S_i-1), которые стали соседями р_i на conv(S_i) (смежные). Обозначим их v₁ и v₂.

3. Вершины conv(S_i-1), которые остаются в conv(S_i) с их соответствующими ребрами.

Ясно, что крайние точки ребра η, пересеченного отрезком р_iр₀, относятся к (1) или (2). Отходя от η (в обе стороны) по списку вершин, представляющему conv(S_i-1), мы можем обнаружить вершины типов (1) и (2). Мы делаем так во времени, линейно зависящем от числа таких вершин. Пока мы так делаем, мы обнаруживаем точки S\S_i,-, которые пересекают уже удаленные ребра, и обновляем их указатели, указывая их или на ребро p_iv₁, или на p_iv₂. Это занимает постоянное время (так как мы должны проверить только два ребра p_iv₁ и p_iv₂) для каждой точки из S\S_i, указатель которой должен быть обновлен (рис. См ниже).

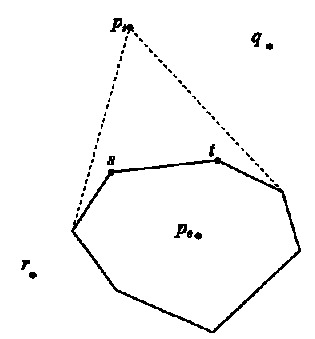
Рис. : Выпуклая оболочка conv(S_i-1). При добавлении p_i, к conv(S_i-1) вершины s и t удаляются, и указатель для точки q должен быть обновлен, в то время как для r - нет.

Какая полная работа выполнена на i-ом шаге? Стоимость удаления ребра conv(S_i-1) равноценна стоимости его создания, так как ребро может быть удалено только однажды после создания. Так как только два ребра создаются на каждом шаге, общее количество этих созданий/удалений ребер (по всем шагам) - в худшем случае 2п.

Что касается стоимости обновления указателей на i-ом шаге, то это число точек р из S\S_i, таких что рр₀ пересекает ребро, которое удаляется на этом шаге. Чтобы ограничить математическое ожидание этой случайной величины, мы прибегаем к обратному анализу. То есть представим, что алгоритм выполняется назад, и будем удалять точку conv(S_i\S₃), чтобы сформировать conv(S_i-1). Тогда число указателей, обновляемых на i-ом шаге первоначального алгоритма, такое же, как число удаляемых на соответствующем шаге обратного алгоритма. Покажем, что ожидаемое число обновляемых указателей есть О(п/i) в зависимости от любого фиксированного множества S_i\S₃, из которого мы удаляем случайную точку на обратном шаге. Так как эта верхняя граница имеет силу для любого множества из i точек, зависимость от конкретного множества S_i\S₃ можно не принимать в расчет.

Для точки , пусть е_р - ребро conv(S_i), пересекаемое рр₀. Вероятность того, что указатель р обновлен — в точности вероятность того, что е_р удалено в результате шага удаления. Ребро е_р удаляется, если одна из двух его вершин удаляется на обратном шаге. Так как точка, удаляемая из S_i, выбрана равномерно из (i-3) точек из S_i\S₃, то эта вероятность есть 0(1/i). Ожидаемое число обновленных указателей - О((п-i)/i), так что полная работа проделанная на этом шаге есть О(п/i). Ключевым моментом здесь является то, что на шаге удаления обратного алгоритма мы удаляем случайную точку из S_i, а не случайную вершину conv(S_i). Теперь используем линейность математического ожидания, чтобы ограничить среднее время работы алгоритма О(п 1оg п).

Теорема: Среднее время работы описанного выше рандомизированного алгоритма для вычисления выпуклой оболочки п точек на плоскости - О(п 1оg п).

Среднее время работы данного алгоритма асимптотически то же, что и время некоторых известных детерминированных алгоритмов выпуклой оболочки, в частности алгоритма Грэхема, рассмотренного выше, и соответствует его нижней оценке.