1. Теоретические материалы

1. Описание задачи и теоретические нижние границы сложности

Два основных варианта задачи построения выпуклой оболочки:

Задача В01 (ВЫПУКЛАЯ ОБОЛОЧКА). В Е^d задано множество S, содержащее N точек. Требуется построить их выпуклую оболочку (т. е. полное описание границы СН(S)).

Задача В02 (КРАЙНИЕ ТОЧКИ). В Е^d задано множество S, содержащее N точек. Требуется определить те из них, которые являются вершинами выпуклой оболочки conv(S).

Рассмотрим задачу В01 о выпуклой оболочке на плоскости. То, что вершины многоугольника, являющегося выпуклой оболочкой, следуют в определенном порядке (в действительности мы можем говорить об упорядоченной выпуклой оболочке), указывает на естественную связь с задачей сортировки. В самом деле, следующая теорема устанавливает тот факт, что любой алгоритм решения задачи В01 должен быть способен выполнять сортировку.

Теорема 3.2. Задача сортировки сводима за линейное время к задаче построения выпуклой оболочки, и, следовательно, для нахождения упорядоченной выпуклой оболочки N точек на плоскости требуется время Q (N log N).

Доказательство. Мы продемонстрируем процедуру сведения, а сформулированное в теореме заключение является следствием утверждения 1 из разд. 1.4 книги ПШ. Пусть заданы N положительных действительных чисел х₁, ..., x_N. Необходимо показать, как можно использовать алгоритм построения выпуклой оболочки для сортировки этих чисел, чтобы при этом дополнительные затраты линейно зависели от количества чисел. Поставим в соответствие числу х_i точку (x_i, x_i²) и присвоим ей номер i (рис. 3.1). Все эти точки лежат на параболе у == x². Выпуклая оболочка этого множества точек, представленная в стандартном виде, будет состоять из списка точек множества, упорядоченного по значению абсциссы. Один просмотр этого списка позволяет прочитать в нужном порядке значения x_i.

Так как для процедуры сведения используются только арифметические операции, то теорема 3.2 остается справедливой во многих вычислительных моделях. А именно в моделях, допускающих умножение, и в которых время, необходимое для сортировки, равно Q(N\ogN). Как указывалось ранее, теорема 3.2 применима в пространствах любой размерности, большей 1 ¹.

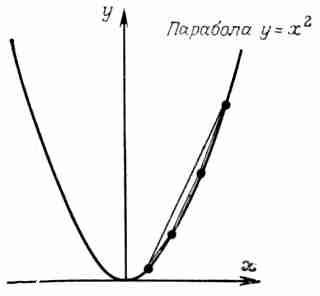
Рис. 3.1. Иллюстрация к доказательству теоремы 3.2.

2. Описание алгоритма Джарвиса

Многоугольник с одинаковым успехом можно задать упорядоченным множеством как его ребер, так и его вершин. В задаче о выпуклой оболочке мы до сих пор обращали внимание главным образом на изолированные крайние точки. А что если вместо этого попытаться определить ребра выпуклой оболочки, приведет ли такой подход к созданию практически пригодного алгоритма? Если задано множество точек, то довольно трудно быстро определить, является или нет некоторая точка крайней. Однако если даны две точки, то непосредственно можно проверить, является или нет соединяющий их отрезок ребром выпуклой оболочки.

Теорема 3.8. Отрезок l, определяемый двумя точками, является ребром выпуклой оболочки тогда и только тогда, когда все другие точки заданного множества лежат на l или с одной стороны от него [Stoer, Witzgall (1970), теорема 2.4.7]. (См. рис. 3.8.)

N точек определяют = 0(N²) прямых. Для каждой из этих прямых можно, используя формулу (3.4), определить за линейное время положение остальных N—2 точек относительно этой прямой и тем самым проверить, удовлетворяет или нет прямая условиям теоремы 3.8. Таким образом, за время 0(N³) можно найти все пары точек, определяющих ребра выпуклой оболочки. Не надо затем большого труда, чтобы расположить эти точки в виде списка последовательных вершин оболочки.

Джарвис заметил, что этот алгоритм можно улучшить, если учесть следующий факт. Если установлено, что отрезок pq является ребром оболочки, то должно существовать другое ребро с концом в точке q [Jarvis (1973)]. В его работе показано, как использовать этот факт, чтобы уменьшить требуемое время до 0(N²). Кроме того, в ней содержится ряд других идей, заслуживающих подробного обсуждения. Здесь будет рассмотрен вариант, включающий изменения, предложенные Эклом [Aki (1979)] и устраняющие небольшие неточности.

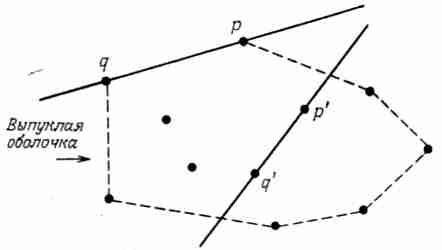
Рис. 3.8. Ребро выпуклой оболочки не может разделять множество точек на части, pq является ребром выпуклой оболочки, так как все точки множества располагаются по одну сторону от него; p'q' не является ребром выпуклой оболочки, так как по обе стороны от него имеются точки.

Предположим, что найдена наименьшая в лексикографическом порядке точка р₁ заданного множества точек. Эта точка заведомо является вершиной оболочки, и теперь хотелось бы найти следующую за ней вершину р₂ выпуклой оболочки. Точка р₂—это точка, имеющая наименьший положительный полярный угол относительно точки р₁ как начала координат. Аналогично следующая точка р₃ имеет наименьший полярный угол относительно точки р₂ как начала координат, и каждая последующая точка выпуклой оболочки может быть найдена за линейное время. Алгоритм Джарвиса обходит кругом выпуклую оболочку (отсюда и соответствующее название — обход Джарвиса), порождая в нужном порядке последовательность крайних точек, по одной точке на каждом шаге (рис. 3.9). Таким образом, строится часть выпуклой оболочки (ломаная линия) от наименьшей в лексикографическом порядке точки (p₁ на рис. 3.9) до наибольшей в лексикографическом порядке точки (p₄ па том же рисунке). Построение выпуклой оболочки завершается нахождением другой ломаной, идущей из наибольшей в лексикографическом порядке точки в наименьшую в лексикографическом порядке точку. Ввиду симметричности этих двух этапов необходимо изменить на противоположные направления осей координат и иметь дело теперь с полярными углами, наименьшими относительно отрицательного направления оси х.

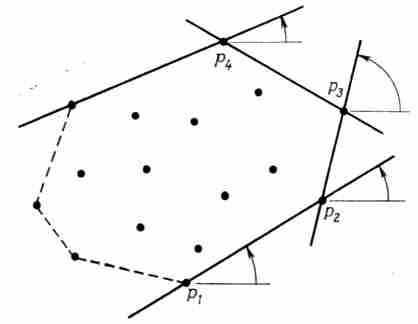
Рис. 3.9. Построение выпуклой оболочки методом Джарвиса. Алгоритм Джарвиса находит последовательные вершины оболочки путем многократного вычисления угла поворота. Каждая новая вершина определяется за время 0(N).