2.Определение устойчивости системы

Теоретические основы

Устойчивость систем, заданных уравнениями состояний, определяют по значениям собственных чисел матрицы состояний A. Система устойчива, если все собственные числа матрицы A имеют отрицательные вещественные части.

Опыт

Для определения собственных чисел в Program CC существует функция eig(A):

CC>A= (-18, -4, 0, 0 ; 0, 0, 1, 0 ; 2, -7, -5, 4 ; 0, -4, 0, -2 )

CC>eig(A)

Значения собственных чисел:

λ₁= -18,033191 + 0j

λ₂= -4,6599604 + 0j

λ₃= -1,1534245 + 2,2991270j

λ₄=-1,1534245 - 2,2991270j

Вещественные части всех собств. чисел отрицательны. Следовательно, система устойчива. На данном этапе уже можно сделать вывод о таком преимуществе метода пространства состояний над классическим частотным подходом, как полная унификация подхода к исследованию многомерных и одномерных систем. Нам не приходится исследовать 4 переходных функции, а всего одну матрицу.

3.Исследование наблюдаемости и управляемости системы.

Теоретические основы

Линейный стационарный объект является вполне (полностью) управляем, если для любой точки x_f из R⁽ⁿ⁾ существует допустимое управлений на конечном интервале [0,t_f], переводящее его из состояния x(0)=0 в состояние x(t_f)=x_f. Для объекта исследования строят матрицу управляемости: ,состоящую из столбцов матрицы B и столбцов матриц A^k-1B (где k=2..n(n-размерность x,m-размерность u)), имеющую размерность (n x nm).

Доказано, что необходимым и достаточным условием управляемости системы, является равенство ранга матрицы управляемости числу n.

Следствия:

• Свойство управляемости не зависит от выбора системы координат в пространстве состояний.

• Если уравнения состояния записано в нормальной форме(см. теоретические основы к п.1), т.е. 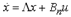, то координата x_j вектора x будет неуправляемой при нулевой j-ой строке матрицы B_n .Система является вполне управляемой при отсутствии нулевых строк в м-це B_n.

Установление возможности определения состояния объекта по измеренным значениям выходной переменной на некотором интервале времени составляет содержание понятия наблюдаемости. Объект называется вполне (полностью) наблюдаемым, если существует такое t1 (t<t1<∞), что по данным измерения y(τ) и u(τ) на интервале t≤ τ≤t1 можно определить состояние x(t).Наблюдаемость- возможность определить состояние по текущим и будущим значениям его входа и выхода. Если текущее состояние можно узнать по прошлым значениям входов и выходов, то говорят о восстанавливаемости объекта. Объект называется вполне (полностью) восстанавливаемым, если существует такое t0 (-∞<t0<t), что по данным измерения y(τ) и u(τ) на интервале t0≤ τ≤t можно определить состояние x(t). Для стационарных систем понятия наблюдаемости и восстанавливаемости совпадают.

Критерием наблюдаемости является равенство ранга матрица наблюдаемости n.

Следствия:

• Свойство наблюдаемости не зависит от выбора системы координат в пространстве состояний.

• Если уравнения состояний записаны в нормальной форме: 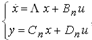, то координата x_j вектора x будет ненаблюдаемой при нулевом j-ой столбце матрицы С_n. Система вполне наблюдаема ,если С_n не содержит нулевых столбцов.

Опыт

1. Исследуем управляемость системы 2 способами:

А)По критерию.

В программе CC построим матрицу управляемости и исследуем её ранг. Для гарантии устойчивости необходимо ,чтобы ранг=4(степени нашей системы)

CC>A= (-18, -4, 0, 0 ; 0, 0, 1, 0 ; 2, -7, -5, 4 ; 0, -4, 0, -2 )

CC>B= (1, 0; 0,0; 0,0; 0,1)

CC>Y=[B A*B A^2*B A^3*B]

CC>rank(Y)

ans = 4

Система является вполне управляемой(ранг=4). Матрица управляемости имеет следующий вид:

Б) Приведением к нормальному виду

Преобразование к нормальной форме выполняется в CC функцией similarity с предварительно «запакованными» матрицами уравнения состояний.

CC>A= (-18, -4, 0, 0 ; 0, 0, 1, 0 ; 2, -7, -5, 4 ; 0, -4, 0, -2 )

CC>B= (1, 0; 0,0; 0,0; 0,1)

CC>C=(0,4,0,0 ; 0,0,0,4)

CC>D=(0,0; 0,0)

CC>p=pack(A,B,C,D)

CC>p1=similarity(p,'eig')

Рассмотрим вид матрицы B в нормальной форме:

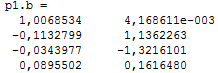
Она не содержит нулевых строк, поэтому система вполне устойчива.

2)Исследуем наблюдаемость системы двумя способами:

А)По критерию:

Составим матрицу наблюдаемости исследуем её ранг:

CC>N=[C' A'*C' (A^2)'*C' (A^3)'*C']

Матрица имеет вид:

Определим её ранг:

CC>rank(N)

ans = 4

Следовательно, система является вполне наблюдаемой.

Б) Приведением к нормальному виду

Выведем матрицу С в нормальном виде:

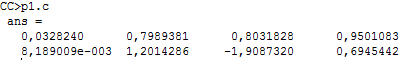
Она не имеет нулевых столбцов, поэтому можно утверждать, что система является вполне наблюдаемой.