Групповые линейные коды

Групповыми линейными кодами называются коды, образующие конечную, абелеву группу над полем Галуа относительно линейной операции над элементами данного поля. Для двоичных кодов эта операция является сложением по модулю два ( ) над полем .

Кодовые слова такого кода содержат символов; причем символов (как правило, начальных) являются информационными, а остальные – проверочными символами. Таким образом, любые кодовые слова данного кода можно записать в виде:

, .

При этом все множество разрешенных кодовых слов равно 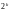и составляет подмножество группы порядка . Следовательно, количество запрещенных (неразрешенных) кодовых слов может быть найдено так: .

Так как разрешенные кодовые слова образуют подгруппу относительно операции сложения, то для определения всех кодовых слов подгруппы достаточно найти линейно независимых кодовых слов. Остальные 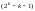кодовых слов находятся сложением этих кодовых слов во всевозможных сочетаниях.

Для формирования линейно-независимых кодовых слов используется производящая матрица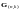 , каноническая форма которой образуется дополнением - столбцов проверочных символов справа к единичной матрице размерности [ ]. Проверочные символы могут быть определены произвольно, однако должны выполняться условия: вес каждой строки производящей матрицы а расстояние между двумя словами и , входящими в матрицу .

Проверочная матрица в каноническом виде записывается дополнением столбцов слева к единичной матрице размерности и позволяет найти синдром ошибки декодируемого кодового слова , где - вектор ошибки.

Синдромом ошибки называется вектор , который определяется выражением:

. (7.15)

Кодовое слово без ошибок имеет нулевой синдром.

Рассмотрим пример. Пусть необходимо построить групповой двоичный код, исправляющий одиночные ошибки , длина кодового слова .

Решение задачи будем осуществлять поэтапно.

1 этап: Определение кодового расстояния .

, примем .

2 этап: Определение количества проверочных элементов производим, используя границу Хэмминга.

, ; , , примем . Скорость кода .

3 этап: Строим производящую матрицу. Проверочные символы записываем так, чтобы расстояния между кодовыми словами и веса этих слов были не меньше трех.

= .

4 этап: Остальные разрешенных кодовых слов находятся путём сложения строк производящей матрицы во всевозможных сочетаниях. Например,

Нулевое слово, хотя и не используется для передачи, также является разрешенным, так как оно определяется как сумма всех остальных разрешенных слов

5 этап: Проверка расстояний между словами полученного кода, в принципе, эквивалентна определению веса каждого разрешенного слова . Нетрудно убедится, что кодовое расстояние построенного кода

6 этап: Проверочную матрицу записываем в виде:

.

Для строк матрицы выбираем такие кодовые слова построенного кода, проверочные символы которых образуют единичную матрицу, а число единиц четно. Получаем три проверочных уравнения:

С помощью этих же уравнений может быть записана и операция кодирования (вычисление проверочных символов):

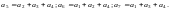
Таким образом, если на вход кодера поступает последовательность вида (1000), то на его выходе кодовое слово: (1000 )=(1000011) = .

7 этап. Допустим, что в канале связи кодовое слово было искажено. Вектор ошибок: . Тогда слово на входе декодера имеет вид: . Применяя к проверочные соотношения, получим:

где – элементы синдрома ошибки.

Сами по себе эти элементы не позволяют сделать вывод о том, какой из кодовых символов был искажен. Однако с помощью элементарной логики устанавливаем, что искажен тот символ, который входит только в 1-ю и 3-ю проверки. Как видно, это символ 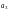. Для исправления ошибки символ инвертируется с помощью последовательности .

Таким образом, на выходе декодера получается оценка декодируемого кодового слова в виде . Если оценка последовательности ошибок точна ( ), то декодированное кодовое слово является переданным кодовым словом . Иначе представляет собой другое разрешенное кодовое слово. Обобщенная схема декодера группового линейного кода показана на рис. 7.1 .

Рис. 7.1 – Структурная схема декодера группового кода

Наиболее сложным элементом декодера, определяющим возможность его реализации, является анализатор синдрома, так как синдромы ошибок используемых на практике кодов могут содержать десятки и сотни элементов, а сложность анализатора обычно увеличивается экспоненциально с ростом длины синдрома. Существенное упрощение процедуры декодирования достигается при использовании кодов Рида–Маллера, Хэмминга и циклических кодов. Коды Рида–Маллера являются линейными кодами с простой процедурой декодирования, осуществляемой одним из методов голосования. Коды Хэмминга, исправляющие одиночные ошибки, могут быть модифицированы таким образом, чтобы синдром ошибки, записанный в виде десятичного числа, указывал номер искаженного символа.