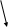- •1. Структурная схема микропроцессора (на примере i8086). Назначение регистров.
- •3. Организация основной памяти.
- •3. Структура и характеристики оперативной памяти
- •4. Модель osi
- •5. Стек протоколов tcp/ip
- •6. Классификация компьютерных сетей
- •7. Данные и модели данных
- •8. Модель данных «сущность-связь»
- •Ограничения целостности
- •9. Реляционная модель данных
- •10. Основные направления исследования в области ии
- •11. Метод резолюции в лппп.
- •12. Продукционная модель
- •13. Основные парадигмы языков программирования.
- •14. Основные понятия ооп: инкапсуляция, наследование, полиморфизм
- •1. Инкапсуляция
- •2. Полиморфизм
- •3. Наследование
- •15. Понятие алгоритма.
- •16. Понятие о временной и емкостной сложности алгоритма
- •17. Машина Тьюринга: детерминированная и недетерминированная
- •18. Понятие формального языка и формальной грамматики
- •19. Основные понятия теории графов.
- •20. Понятие количества информации и энтропии. Теорема Шеннона.
- •21. Деревья в теории графов.
- •22. Модели линейного программирования (постановка задачи, математическая модель, решение графическим методом).
- •23. Двойственность в задачах линейного программирования.
- •25. Элементы теории игр.
- •2. Подпрограммы. Процедуры и функции
- •3. Массивы
- •4. Записи
- •5. Работа с Динамическими данными
- •6. Динамические структуры данных. Линейные списки.
- •7. Динамические структуры данных: двоичные деревья
- •8. Работа с файлами
- •9.Операции целочисленной арифметики
- •10. Системы счисления. Перевод чисел из одной системы счисления в другую
- •11. Язык sql. Назначение и основные команды.
- •Манипулирование данными
- •Простые запросы
- •12. Алгоритмы внутренней сортировки.
- •13. Алгоритмы внешней сортировки
- •14. Нахождение кратчайших путей в графе
- •15. Поиск в ширину
- •16. Поиск остова и минимального остова.
- •17. Линейная модель работы информационно-поисковой системы.
- •18. Хеширование
- •Основные достоинства в-дерева
- •20. Логические вопросно-ответные системы:выполнение запросов различных типов.
- •21. Поиск в семантической сети.
- •22. Принципы динамического программирования. Иллюстрация на примере.
- •23. Адресация в Интернете
- •Доменные имена
- •Общий вид формата url-адреса
- •Как работает dns-сервер
- •24. Основные сервисы в сети Интернет.
- •Word Wide Web (www) - "Всемирная паутина"
- •Поиск информации в сети
- •VoIp сервис
- •Мессенджеры
- •25. Использование html. Структура Web(html) страницы.
18. Хеширование
Понятие хэш-таблицы и хеш-функции. Коллизии и их разрешение.
Идея этого метода состоит в отыскании функциональной зависимости k=f(x), которая бы позволяла за не зависящие от длины входа время (т.е. за 1 шаг) вычислить адрес блока, в котором физически находится искомая запись со значением искомого поля, равном x. Но в такой постановке задача в общем случае неразрешима. Поэтому приходиться воспользоваться хэш-таблицей. Хэш-таблица представляет из себя массив hash, такой что
hash[m]=k, если k – адрес блока, в котором хранится запись со значением поискового поля, равным x, а m=h(x), где h(x) - некоторая функция, вычисляемая за 1 шаг, и называемая хэш-функцией.
Тогда алгоритм хэширования выглядит так:
m:=h(x); k:=hash[m];
Конечно, перед тем как выполнять поиск, следует сформировать хэш-таблицу:
for x {множество поисковых значений} do hash[h(x)]:=block(x); // block(x) - блок, где находится запись со значением поискового поля, равным x
Однако, на практике построение такого алгоритма возможно только при условии, что функция h – биекция, т.е.
А) х,у [ (h(x)=h(y)) –> (x=y)]-условие инъективности
B) m {m} x h(x)=m – условие сюръективности
Очевидно, что условие B эквивалентно условию С:
С) х h(x)=1..n т.е. ({m}=1..n)
Для любых x,y (h(x)=h(y)=>x=y) – условие инъективности.
для любого m из {m} сущ. x, что h(x)=m. – условие сюръективности.
Очевидно, что условие B эквивалентно условию С:
С) для любого х - h(x)=1..n ({m}=1..n), если все элементы х различны и выполняется условие A.
Следует попытаться добиться выполнения условий A и С. Но это в общем случае невозможно. Чем же грозит невыполнение этих условий? Если нарушается условие «A», то существуют две различные записи со значениями поисковых полей x и у такими, что h(x)=h(y)=m. Пусть k и l – адреса блоков, где хранятся эти записи. Тогда hash[m]=k и hash[m]=l, что реализовать напрямую невозможно. Такая ситуация называется коллизией. Последствия невыполнения условия C менее серьезны, они приводят к увеличению памяти, требуемой на хранение хэш-таблицы. В принципе на это можно пойти, если увеличение не будет слишком чрезмерным. Однако даже добиться только выполнения условия A в общем случае не представляется возможным, поэтому на практике приходится использовать специальные приемы для разрешения коллизий. Очевидно, что они зависят от выбора функции h(x).
Путем всестороннего теоретического и практического исследования проблемы установлено, что оптимальная функция хеширования для целочисленных полей
h(x)=x mod q + 1,
где q – наименьшее простое число среди >=n. Тогда 1<=h(x)<=n.
Если x – не числовое значение, то сначала вычисляется каким-либо способом числовое значение, и оно уже применяется в хеш-функции.
Для разрешения коллизий используются различные методы, такие как метод цепочек, методы линейных и квадратичных проб и т.д.
Одним из недостатков хеширования является трудность поиска по неключевым полям, так как в этом случае неизбежны естественные коллизии.
Метод цепочек.
Метод цепочек подразумевает то, что в каждую ячейку хеш-таблицы действительно должно быть записано несколько значений. Конечно, «в лоб» это сделать просто невозможно, поэтому в ячейках хранятся не сами адреса элементов (точнее блоков), а указатели на списки адресов. В случае коллизии такой список будет содержать несколько значений.
Пример.
Метод цепочек
-
ФИО
Телефон
Аdr1 Баранов
111-111
Аdr2 Мигунова
444-444
Adr3 Фоминых
777-777
Adr4 Онищенко
666-666
Adr5 Одинцова
555-555
Adr6 Коротаев
333-333
Adr7 Гоголев
222-222
h(‘Баранов’)=5
h(‘Гоголев’)=3
h(‘Коротаев’)=2
h(‘Мигунова’)=5
h(‘Онищенко’)=2
h(‘Одинцова’)=6
h(‘Фоминых’)=5
Разрешение коллизий методом цепочек
При поиске следует последовательно просматривать записи по всем блокам, занесенным в список. Обратим внимание, что в наихудшем случае в список могут быть занесены все блоки, но, как показывает анализ, этот случай очень маловероятен.
В качестве недостатка также следует отметить необходимость лишней операции, связанной с доступом к списку по адресу (эти проблемы излагаются в дисциплине «Программирование», см. также [9, 10]).
Метод открытой адресации.
Метод открытой адресации предполагает несколько иной подход.
Имеется обычная хеш-таблице. В процессе ее заполнения, при получении нового значения, мы его заносим в том случае, если данная ячейка еще не заполнена (например, значение равно нулю). В противном случае предполагается занесение значения в другую ячейку, вычисляемую по какому-либо алгоритму, но если и она оказывается уже заполненной, то вычисляется еще одна ячейка и т.д.
Очевидно, что на самом деле существует столько конкретных методов открытой адресации, сколько алгоритмов перевычисления ячеек можно предложить.
Один из таких подходов называется методом линейных проб. Этот метод предполагает для вычисления заполняемой ячейки в случае коллизии использование функций :
h(x)=x mod q +1;
h1(x)=(x+1) mod q +1;
h2(x)=(x+2) mod q + 1;
h3(x)=(x+3) mod q + 1;
…………………………………
То есть, попросту говоря, если вычисленная ячейка оказалась занятой, то используем соседнюю ячейку справа и т.д., при этом для последней ячейки роль соседней справа выполняет первая ячейка. При поиске, кроме текущего значения, следует просматривать и ячейки справа от текущей до тех пор, пока мы не достигнем пустой ячейки.
Очевидно, что эффективность метода тем выше, чем меньше ячеек приходится просмотреть при заполнении и поиске. Метод линейной адресации оказывается неэффективным, так как данные часто имеют свойства группироваться вокруг определенных значений. Например, возраст преподавателей, может группироваться либо в пределах 50-60 лет, либо 25-30 лет, и подобные закономерности часты. Таким образом, при переадресации внутри хеш-таблицы следует стремиться к максимальному расширению области затрагиваемых ячеек.
Метод квадратичных проб состоит в том, что если возникает коллизия, используем функции
h(x)=x mod q +1;
h1(x)=(x+1) mod q +1;
h2(x)=(x+22) mod q + 1;
h3(x)=(x+32) mod q + 1;
…………………………………
Здесь обязательно выполнение условия «простоты» числа q, иначе алгоритм, как доказано, может зациклить. Этот метод устраняет основной недостаток метода линейных проб и является наиболее часто используемым.
Алгоритм формирования хэш-таблицы выглядит так:
for i:=1 to q do hash[i]:=0;
for x {множество поисковых значений} do begin
j:=0;
while hash[(x+j*j) mod q]<>0 do inc(j);
hash[(a[i]+j*j) mod q]:=block(x);// блок, где находится запись с x
end;
А алгоритм поиска выглядит так:
j:=0;
while (hash[(x+j*j) mod q]<>0) and (a[hash[(x+j*j) mod q ]]<>x) do inc(j);
if hash[(x+j*j) mod q]<>0 then return(hash[(x+j*j) mod q]);
Приведем пример.
Метод квадратичных проб
-
0
1
2
3
4
5
6
Adr7
Adr5
Adr3
Adr4
Adr6
Adr1
Adr2
m=7
Хеширование с использованием квадратичных проб требует 3 операции в среднем и n операций в наихудшем, таким образом, T~n, Tср~const. Для построения хэш-таблицы: T~n2, Tср~const.
19. B-дерево.
Разреженный индекс строится для плотного индекса, но если записи разреженного индекса поддерживать в отсортированном порядке, то возникнет проблема перестроения разреженного индекса при каждой модификации, что неизбежно приведет к высоким затратам. Действительно, неизбежно m>=n/e. Но, к счастью, существует эффективное решение.
Можно строить разреженный индекс для разреженного индекса, для которого в свою очередь также строить разреженный индекс и т.д. Таким образом, можно добиться, чтобы разреженный индекс самого верхнего уровня (корень) имел параметр m<=e. Такая структура называется B-деревом. Для каждого блока в B-дереве число записей k подчиняется условию (e+1)/2<=k<=e, где e – максимальное число записей в блоке. Исключение составляет корневой блок, для которого 1<=k<=e.
Перед включением
-
 .
.6
.
(1,3),(2,1),(6,7) |
(7,6),(8,5) |
А)Включаем (9,2)
-
.
6
.
(1,3),(2,1),(6,7) |
(7,6),(8,5),(9,2) |
В)Включаем (5,4)
-
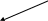 .
.2
.
6
 .
.
(5,4),(6,7) |
(1,3),(2,1) |
(7,6),(8,5),(9,2) |
Рис. 26. Включение в разреженный индекс
Вставка элемента в B-дерево и удаление из B-дерева предполагают соответственно вставку в разреженный индекс и удаление из разреженного индекса низшего уровня, при этом может потребоваться коррекция индекса более высокого уровня (в случае нарушения условий) и т.д.
|
|
11 |
|
25 |
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
4 |
|
11 |
|
27 |
|
35 |
|
(26,1),(27,3) |
(39,5),(41,7) |
(9,6),(10,8) |
(1,7),(3,5) |
(30,11),(32,12),(35,7) |
|
15 |
|
19 |
|
25 |

(12,2),(14,1) |

(21,11),(24,8) |
(16,9),(19,4) |
Рис. 27. B-дерево
Рассмотрим примеры.
A) Вставим в дерево, изображенное на рис. 26 элемент (2,4) (рис. 28)
|
|
11 |
|
25 |
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
4 |
|
11 |
|
27 |
|
35 |
|
(26,1),(27,3) |
(39,5),(41,7) |
(9,6),(10,8) |
(1,7),(2,4),(3,5) |
(30,11),(32,12),(35,7) |
|
15 |
|
19 |
|
25 |
(12,2),(14,1) |
(21,11),(24,8) |
(16,9),(19,4) |
Рис. 28. Вставка в B-дерево
B) Вставим теперь элемент (4,9) (рис. 29)
|
|
11 |
|
25 |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
27 |
|
35 |
|
|
2 |
|
4 |
|
11 |
(26,1),(27,3) |
(39,5),(41,7) |
(9,6),(10,8) |
(1,7),(2,4) |
(3,5),(4,9) |
(30,11),(32,12),(35,7) |
|
15 |
|
19 |
|
25 |
(12,2),(14,1) |
(21,11),(24,8) |
(16,9),(19,4) |
Рис. 29. Вставка в B-дерево
С) Удалим элемент (32,12) (рис. 30)
|
|
11 |
|
25 |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
27 |
|
35 |
|
|
2 |
|
4 |
|
11 |
(26,1),(27,3) |
(39,5),(41,7) |
(9,6),(10,8) |
(1,7),(2,4) |
(3,5),(4,9) |
(30,11),( 35,7) |
|
15 |
|
19 |
|
25 |
(12,2),(14,1) |
(21,11),(24,8) |
(16,9),(19,4) |
Рис. 30. Удаление из B-дерева
D) Удалим элемент (30, 11) (рис. 31)
|
|
11 |
|
25 |
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||
|
|
|
|
||||||||
|
35 |
|
|
2 |
|
4 |
|
11 |

(9,6),(10,8) |
(39,5),(41,7) |
(1,7),(2,4) |
(3,5),(4,9) |
|
15 |
|
19 |
|
25 |
(26,1),(27,3),(35,7) |
(12,2),(14,1) |
(21,11),(24,8) |
(16,9),(19,4) |
|
|
1 |
|
25 |
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
25 |
|
35 |
|
|
2 |
|
4 |
|
11 |
(39,5),(41,7) |
(9,6),(10,8) |
(21,11),(24,8) |
(1,7),(2,4) |
(3,5),(4,9) |
|
15 |
|
19 |
|
(26,1),(27,3),(35,7) |
(12,2),(14,1) |
(16,9),(19,4) |
Рис. 31. Удаление из B-дерева
Сбалансированность означает, что длина пути от корня дерева к любому его листу одна и та же.
Ветвистость дерева — это свойство каждого узла дерева ссылаться на большое число узлов-потомков.







 1
1