12.7 Охлаждение (нагревание) шара

Рассмотрим охлаждение шара в среде с постоянной температурой t_cp и постоянным коэффициентом теплоотдачи α. В начальный момент времени при τ = 0 все точки шара с радиусом r₀ имеют одинаковую температуру t₀. Теплофизические параметры λ, С_р, ρ не зависят от температуры и считаются известными. При заданных условиях температура для любой точки шара будет функцией только времени и безразмерной координаты R = r/r₀.

Также требуется найти распределение температуры внутри шара, т.е. уравнение температурного поля.

Если обозначить текущую избыточную температуру для любой точки шара J = t - t_ср, то дифференциальное уравнение теплопроводности шара в сферических координатах запишется:

(12.35)

Геометрические и физические условия заданы.

Начальные условия: при τ = 0; J₁ = t - t_ср для всех точек шара.

Граничные условия:

На поверхности шара при r = r₀; .

Из условия симметрии задачи в центре шара при r = 0: .

Решая уравнение (12.35) методом разделения переменных и, подчиняя полученное решение начальным и граничным условиям, после ряда преобразований для Fo ≥ 0,3 получим:

(12.36)

Т.к. μ в уравнении (12.36) зависит только от числа Bi, то уравнение температурного поля в общем виде:

Θ = f (Fo, Bi, R).

Для центра шара: Θ_R=0 = f₁ (Fo, Bi) (12.37)

Для поверхности шара: Θ_R=1 = f₂ (Fo, Bi) (12.38)

Функции, определяемые выражениями (12.37) и (12.38) для различных значений Fo и Bi представлены в виде номограмм.

Аналогично, как для пластины и цилиндра начальная избыточная внутренняя энергия шара:

(12.39)

Количество теплоты, которое отдается или воспринимается шаром за промежуток времени от τ = 0 до τ₁, также можно определить по номограмме, которая построена по функции вида: Q/Q₀ = f (Bi, Fo)/

12.8 Охлаждение (нагревание) тел конечных размеров

12.8.1 Охлаждение параллелепипеда

Р

Z

ассмотрим охлаждение параллелепипеда в среде с постоянной температурой (t_ср) и с постоянным коэффициентом теплоотдачи  на всех его гранях. В начальный момент времени (=0) все точки параллелепипеда имеют одинаковую температуру (t₀).

Y

X

- X

0

2_y

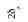
- Z

- Y

2_x

Рисунок 12.7 К охлаждению параллелепипеда

Параллелепипед c размерами 2d_x  2d_у ´ 2d_z является однородным и изотропным.

Требуется найти распределение температуры в параллелепипеде для любого момента времени, а также среднюю температуру, необходимую для определения количества отведенной (подведенной) теплоты.

Поместим начало координат в центре параллелепипеда. При этом дифференциальное уравнение запишется следующим образом:

(12.40)

Нахождение аналитического решения этого уравнения, дополненного условиями однозначности, представляет собой довольно сложную задачу.

Параллелепипед конечных размеров можно рассматривать как тело, образованное пересечением соответственно трех взаимно перпендикулярных неограниченных пластин конечной толщины.

Доказано, что решение таких задач представляется произведением безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.

Параллелепипед образован в результате пересечения трех взаимно перпендикулярных неограниченных пластин конечными толщинами 2d_x, 2d_у, 2d_z. Следовательно, для него и решение можно представить как произведение безразмерных температур для трех безграничных пластин:

 = _x  _y  _z (12.41)

Множители в уравнении (12.41) могут быть рассчитаны по уравнению (12.20) или определены по номограммам.

Этот метод известен в теории теплопроводности под названием теоремы о перемножении решений.

Полученное решение справедливо и для нахождения средней температуры:

(12.42)

Множители в уравнении (12.42) находятся по формуле (12.27).

12.8.2 Охлаждение (нагревание) длинного прямоугольного стержня

Поперечное сечение стержня представляет собой прямоугольник с размерами 2δ_х × 2δ_у. Такое тело можно рассматривать как результат взаимного пересечения двух неограниченных пластин толщиной 2δ_х и 2δ_у, условия однозначности для которых такие же, как и для образовавшегося стержня. Безразмерное температурное поле для поставленной задачи:

Q = Q_x × Q_y (12.43)

Множители в уравнении (12.43) также могут быть рассчитаны по уравнению (12.20) или определены по номограммам.

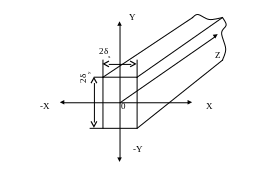
Рисунок 12.8 К охлаждению полуограниченного прямоугольного стержня

12.8.3 Охлаждение цилиндра конечной длины

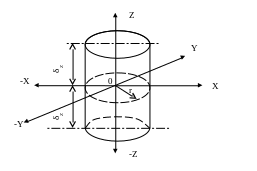
Рисунок 12.9 К охлаждению цилиндра конечной длины

Цилиндр конечной длины можно рассматривать как результат пересечения безграничного цилиндра радиусом r₀ и пластины толщиной 2δ_Z. Следовательно, и безразмерную температуру для такого тела можно записать как:

Q = Q_r × Q_z (12.44)

Полученные решения для полуограниченного прямоугольного стержня и цилиндра конечной длины (формулы 12.43 и 12.44) справедливы и для нахождения средних температур.

Кроме того, следует подчеркнуть, что все решения, полученные выше справедливы как для охлаждения, так и для нагрева тел неограниченных и конечных размеров.