10.Теорема о размерности линейной оболочки строк (столбцов) матрицы.

Теорема 3.6. Размерность линейной оболочки строк (столбцов) матрицы А равна ее рангу.

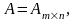
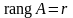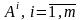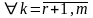
Доказательство проведем для строк матрицы. Пусть , и пусть базисный минор матрицы А расположен в первых r ее строках. Обозначим, как и раньше, – строки матрицы А. Тогда по теореме о базисном миноре система линейно независима, и 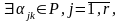такие, что 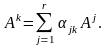Дальше точно так же, как и при доказательстве теоремы 3.5, показываем, что 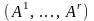- система образующих в , а значит, и базис, и поэтому 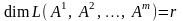. Для столбцов доказательство проводится аналогично. 

11. Сумма и пересечение подпространств линейного пространства. Теорема о сумме и пересечении подпространств.

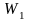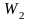Определения. Пересечением подпространств и линейного пространства V над P называется его подмножество

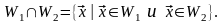
Суммой подпространств и называется подмножество

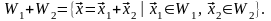
Сумма подпространств называется прямой и обозначается если .

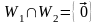Теорема 3.7. Сумма и пересечение подпространств линейного пространства также являются его подпространствами.

►Пусть и – подпространства линейного пространства V над P. Тогда

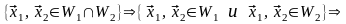
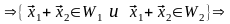
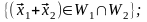
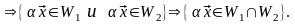
Таким образом, выполняются условия теоремы 3.4, значит, 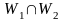– подпространство пространства V.

Докажем теперь, что сумма подпространств – подпространство. Действительно,

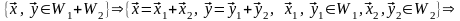
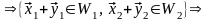
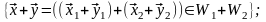
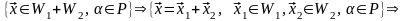
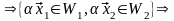
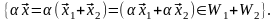
Итак, в этом случае условия теоремы 3.4 также выполняются, и поэтому, 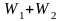– также подпространство пространства V. 

12. Теорема о размерности прямой суммы.

Теорема 3.8. Размерность прямой суммы подпространств равна сумме их размерностей.

►Пусть и – подпространства линейного пространства V над P, , 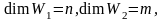и пусть

– (3.38)

базис , а

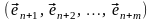– (3.39)

базис . Покажем, что

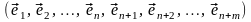– (3.40)

базис .

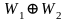Действительно, 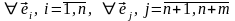: 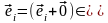, 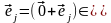.Кроме того,

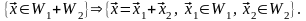
Тогда 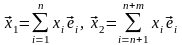, значит, ,

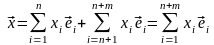и, таким образом, (3.40) – система образующих в .

Линейную независимость (3.40) докажем на основании определения.

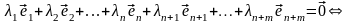
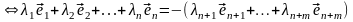. (3.41)

Вектор в левой части (3.41) принадлежит пространству , а в правой – пространству . Так как сумма прямая, то , поэтому

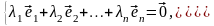
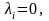
На основании линейной независимости (3.38) и (3.39), получаем 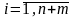, откуда и вытекает линейная независимость (3.40). Таким образом, (3.40) – линейно независимая система образующих пространства , а значит, и его базис, и поэтому

.

13. Определение матрицы перехода и её свойства.

Пусть в линейном пространстве заданы два базиса:

(3.41)

и

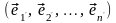. (3.42)

Принадлежность вектора второму базису отмечается штрихом, причем удобно штрих ставить не на вектор, а на индекс, например, 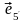– пятый вектор второго базиса. Тогда каждый из векторов второго базиса можно разложить по первому. Все координаты будем обозначать одной и той же ключевой буквой t с двумя индексами: нижним индексом обозначим номер разлагаемого вектора, а верхним – номер координаты. Таким образом,

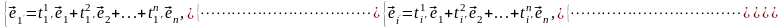(3.43)

Учитывая нашу договоренность, систему равенств (3.43) можно сокращенно записать одним равенством:

(3.44)

(оцените красоту записи!)

Введем следующие обозначения:

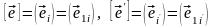
(подчеркиваем, что это матрицы-строки)

.

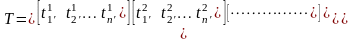Тогда 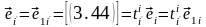=[располагаем по правилу цепочки] = 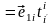, откуда вытекает, что

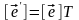. (3.45)

Матрицей перехода от базиса (3.41) к базису (3.42) называется матрица Т = 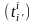, столбцами которой являются координатные столбцы векторов второго базиса в первом базисе, т. е. матрица, удовлетворяющая системе равенств (3.43) или (3.44), либо одному матричному равенству (3.45).