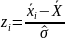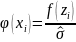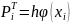- •Министерство культуры российской федерации
- •«Санкт-петербургский государственный университет кино и телевидения»
- •Введение
- •Исходные данные
- •Вычисление основных выборочных характеристик.
- •Ранжирование выборочных данных и вычисление моды и медианы.
- •Вычисление интервальных оценок для математического ожидания и дисперсии.
- •Параметрическая оценка функции плотности распределения.
- •Проверка гипотезы о нормальном распределении случайной величины по критерию Пирсона.
- •Список литературы
Вычисление интервальных оценок для математического ожидания и дисперсии.
Интервальная оценка для математического ожидания случайной величины Х. Информативный способ оценивания состоит в построении интервала, в котором с заданной степенью достоверности окажется оцениваемый параметр.
Формула вычисления интервальной оценки для математического ожидания:
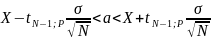 ,
,
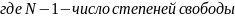
Р – доверительная вероятность, которую необходимо выбрать:
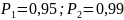
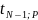 -
значение t
– распределение Стьюдента для N-1
степени свободы и выбранной доверительной
вероятности
-
значение t
– распределение Стьюдента для N-1
степени свободы и выбранной доверительной
вероятности
Для
 находим
по таблице распределения Стьюдента(таблице
5 методических указаний)
находим
по таблице распределения Стьюдента(таблице
5 методических указаний)
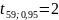
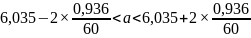
 6,278426
6,278426
Для
 находим по таблице
находим по таблице
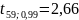
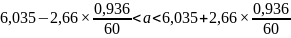
|
5,710467 |
< a < |
6,358866 |
|
Интервальная оценка для дисперсии случайной величины Х.
Формула вычисления интервальной оценки для дисперсии.
Интервальную оценку для дисперсии можно найти по формуле:

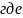
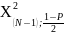 и
и
 - значения функции
- значения функции
 распределение при выбранной доверительной
вероятности
распределение при выбранной доверительной
вероятности
 и заданной степени свободы v:
N-1
и
и заданной степени свободы v:
N-1
и
 ,
,
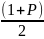 (найдем по табл.6 методических указаний)
(найдем по табл.6 методических указаний)
Задаемся
доверительной вероятностью

Для получаем: =0,025; =0,975
Находим
по таблице:
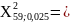 40,4817;
40,4817;
 83,2976
83,2976
Найдем
интервальную оценку для дисперсии :
:
|
|
|

Для получаем: =0,005; =0,995
Находим
по таблице:
 35,5346;
35,5346;
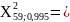 91,9517
91,9517
Найдем интервальную оценку для дисперсии :
0,57188 |
< < |
1,479834 |
Параметрическая оценка функции плотности распределения.
Будем исходить из предположения, что полученная выборка имеет нормальный закон распределения с плотностью вероятностей, заданной в виде:
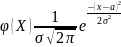
где
а
-
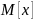 -
математическое ожидание,
-
математическое ожидание,
- дисперсия.
Заменяя
в формуле математическое ожидание и
дисперсию их оценками, найденными по
выборке, получим оценку предполагаемой
модели закона нормального распределения,
которая называется параметрической,
так как определяется двумя параметрами
Х и
 .
Параметрическая оценка неизвестной
функции плотности, построенная в
предположении, что допустима нормальная
модель, имеет вид:
.
Параметрическая оценка неизвестной
функции плотности, построенная в
предположении, что допустима нормальная
модель, имеет вид:

где
-
середина
i-го
частичного интервала [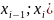 .
.
Значения
функции (теоретическая
плотность распределения) вычисляем в
тех же самых точках, в которых вычисляли
функцию
по экспериментальным данным.
(теоретическая
плотность распределения) вычисляем в
тех же самых точках, в которых вычисляли
функцию
по экспериментальным данным.
Для того, чтобы облегчить вычисление перейдем от переменной к переменной z по формуле:
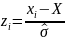
Определив
значения z
по таблице 11 в методических указаниях
находим значения функции плотности
стандартной нормальной величины
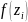 .
Разделив
.на
.
Разделив
.на
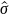 получим значение функции
получим значение функции
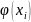 .
.
Вычисления теоретической плотности распределения, а также теоретических вероятностей и частот предоставлены в таблице 3.
Таблица 3
Результаты вычисления теоретических вероятностей и частот.
h |
|
|
|
|
|
|
|
|
[3,73;4,33) |
1 |
4.03 |
-2.141 |
0.0404 |
0.0432 |
0.0259 |
1.554 |
2 |
[4,33;4,93) |
6 |
4.36 |
-1.500 |
0.1295 |
0.1383 |
0.0830 |
4.980 |
5 |
[4,93;5,53) |
13 |
5.23 |
-0.860 |
0.2756 |
0.2944 |
0.1766 |
10.598 |
11 |
[5,53;6,13) |
10 |
5.83 |
-0.219 |
0.3894 |
0.4159 |
0.2496 |
14.974 |
15 |
[6,13;6,73) |
17 |
6.43 |
0.422 |
0.3653 |
0.3902 |
0.2341 |
14.047 |
14 |
[6,73;7,33) |
8 |
7.03 |
1.063 |
0.2275 |
0.2430 |
0.1458 |
8.748 |
9 |
[7,33;7,93) |
3 |
7.63 |
1.704 |
0.0940 |
0.1004 |
0.0602 |
3.615 |
4 |
[7,93;8,53) |
2 |
8.23 |
2.345 |
0.0252 |
0.0269 |
0.01162 |
0.969 |
1 |
|
60 |
|
|
|
|
0.9914 |
59.485 |
59 |
В
первом столбце помещены к – частичных
полуинтервалов, во втором – наблюдаемые
частоты
,
в третьем – координаты середины частичных
интервалов, в четвертом – значения
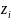 ,
которые используются для нахождения
функций
по таблице 11 методических указаний. В
пятом столбце помещены значения плотности
вероятностей, отнесенные к середине
частичных интервалов в шестом и седьмом
– теоретические вероятности и частоты,
отнесенные к середине частичных
интервалов. В восьмом столбце – вероятные
реальные теоретические частоты.
,
которые используются для нахождения
функций
по таблице 11 методических указаний. В
пятом столбце помещены значения плотности
вероятностей, отнесенные к середине
частичных интервалов в шестом и седьмом
– теоретические вероятности и частоты,
отнесенные к середине частичных
интервалов. В восьмом столбце – вероятные
реальные теоретические частоты.
Сумма
всех значений теоретических вероятностей
в интервале
 равна
равна
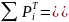 0,9914,
а сумма теоретических частот
0,9914,
а сумма теоретических частот
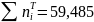 .
Это указывает на необходимость вычислить
дополнительные значения вероятностей
слева и справа от заданного интервала,
чтобы выполнялось условие
.
Это указывает на необходимость вычислить
дополнительные значения вероятностей
слева и справа от заданного интервала,
чтобы выполнялось условие
 .
Дополняем слева и справа по два интервала
и проводим необходимые расчеты.
.
Дополняем слева и справа по два интервала
и проводим необходимые расчеты.
Таблица 4
Дополнительные интервалы
h |
|
|
|
|
|
|
|
|
[2,53;3,13) |
- |
2,83 |
-3,423 |
0,0012 |
0,0011 |
0,0007 |
0,040 |
- |
[3,13;3,73) |
- |
3,43 |
-2,782 |
0,0084 |
0,0079 |
0,0047 |
0,283 |
- |
[8,53;9,13) |
- |
8,83 |
2,986 |
0,0046 |
0,0043 |
0,0026 |
0,155 |
- |
[9,13;9,73) |
- |
9,43 |
3,627 |
0,0005 |
0,0005 |
0,0003 |
0,017 |
- |
|
|
|
|
|
|
1 |
60 |
|
В
результате получаем, что сумма вероятностей
по всем частичным интервалам, лежащим
в границах [2,53;9,73)
равна
,
а сумма всех частот по всем частичным
интервалам
 .
Это указывает на то, что все вычисления
выполнены обоснованно и с достаточной
точностью.
.
Это указывает на то, что все вычисления
выполнены обоснованно и с достаточной
точностью.
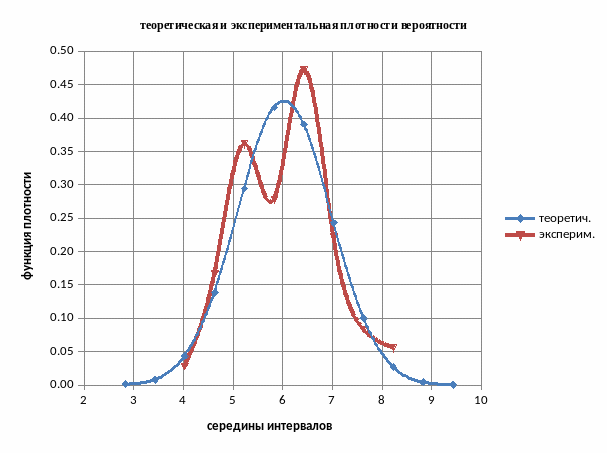
Для того, чтобы иметь наглядное представление о том, как изменяется экспериментальная и теоретическая плотность нормального распределения, строят их графики (рис.1).
|
2,83 |
3,43 |
4.03 |
4.36 |
5.23 |
5.83 |
6.43 |
7.03 |
7.63 |
8.23 |
8,83 |
9,43 |
|
0,0011 |
0,0079 |
0.0432 |
0.1383 |
0.2944 |
0.4159 |
0.3902 |
0.2430 |
0.1004 |
0.0269 |
0,0043 |
0,0005 |
|
|
|
0,028 |
0,167 |
0,361 |
0,278 |
0,472 |
0,222 |
0,083 |
0,056 |
|
|
Рис.1