6.1. Принцип максимума в задаче о быстродействии.
В
этой задаче время T
не фиксировано и
(X,U)
= 1 (в данном
случае),
т.е.
J
=
=T
Функция Гамильтона:
=
+
Т.к.
функции
(X,U)
,
=
не зависят от
,
получим:
=
=
0
=
const
*см. гамильтонову систему
Максимум
функции
реализуется одновременно с максимумом
функции H=
Из
требования
0 (принцип
максимума) следует,
что максимум H
0
*в
момент времени T, т.к.
должен
быть равен 0 в T.
Таким образом, для оптимальности по быстродействию необходимо:
Существование ненулевой непрерывной вектор - функции:
(t)
=
,
составляющие которой удовлетворяют
системе:
=
;
=
Чтобы функция Гамильтона H = ( (t), F (X,U)) достигала при каждом значении
0 < t < T максимума по U.
Чтобы при t = T max H = ( (t), F (X,U)) 0 .
Замечание:
Оказывается, что если выполняются условия 1 и 2, то функция max H(t) постоянна,
так что условие 3 справедливо в любой момент времени 0 < t < T.
Пример:
Рассмотрим задачу о предельном быстродействии при переходе системы
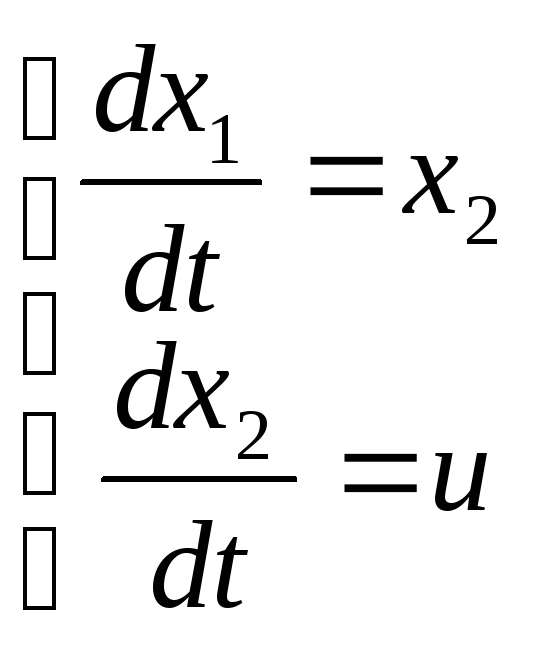из
начального состояния
в заданное состояние
*т.е. осуществляется переход в нулевое состояние.
Единственное управляющее воздействие u ограничено по модулю
(*)
Составляем
функцию Гамильтона: H =
+
Составляющие вектора должны удовлетворять уравнениям:
=
0;
=
Интегрирование дает:
=
,
=
и функция Гамильтона:
H
=
+
Максимум
функции Гамильтона H при ограничении
(*) достигается при управляющем воздействии:
u(t) =
sign(
)
=
sign
(**),
а
величина
=
+
(
)sign(
)
Из выражения (**) следует:
При оптимальном процессе управляющее воздействие в любой момент времени равно одному из двух своих предельных значений (+
,
),
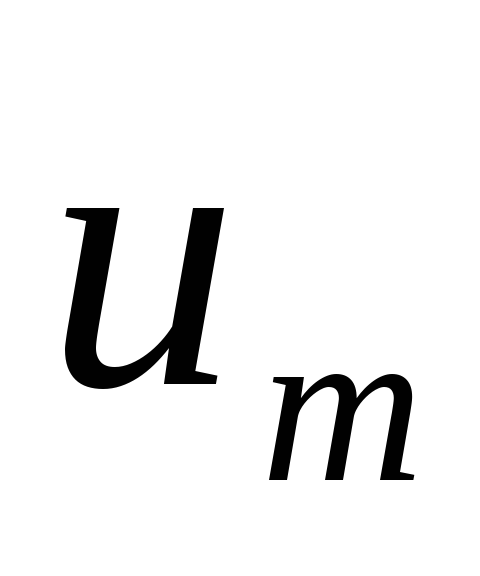т.е. значениям на границе области
возможных управлений.
Этот
вывод , вытекающий из принципа максимума,
не может быть получен методами
классического вариационного исчисления.
Обычно считают
=1
Оптимальный процесс состоит не более чем из двух интервалов, т.к. функция
=
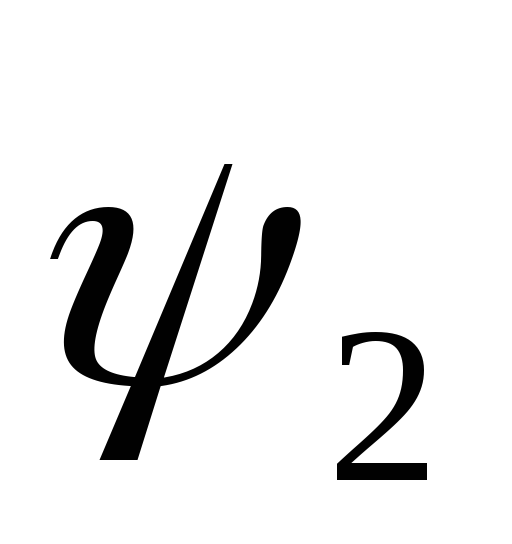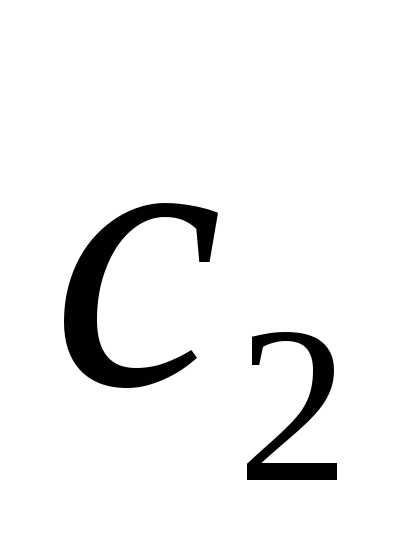
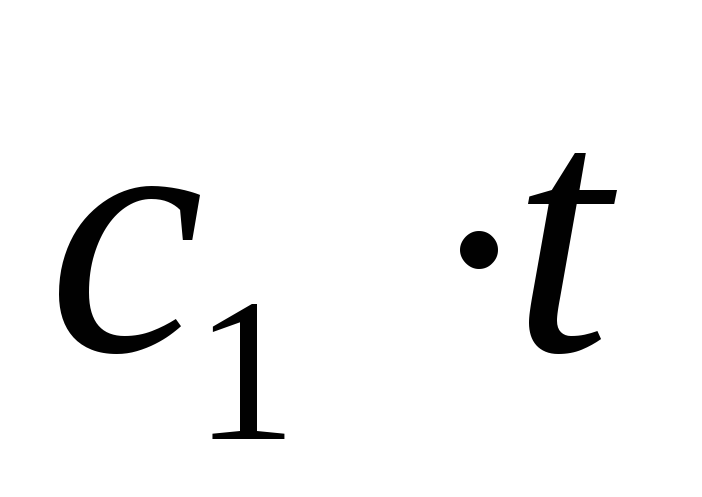не
более одного раза переходит через 0,
меняя при этом свой знак
Решаем исходную систему:
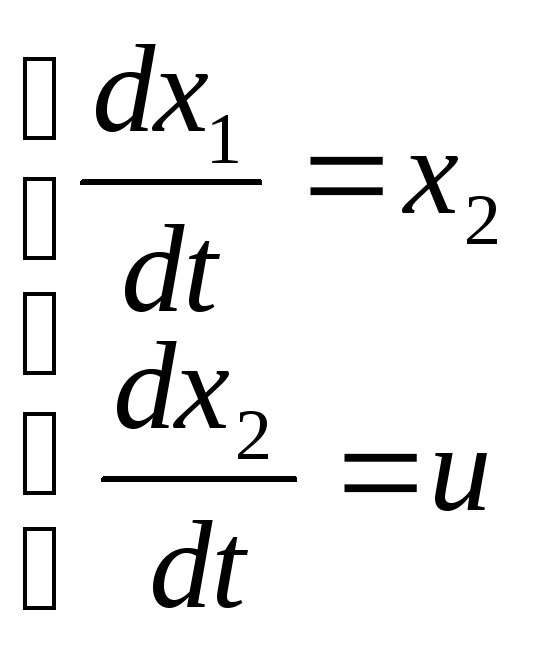
1). Пусть u = 1,
тогда
(t)
= t +
(t)
=
+
+
=
+
=
+
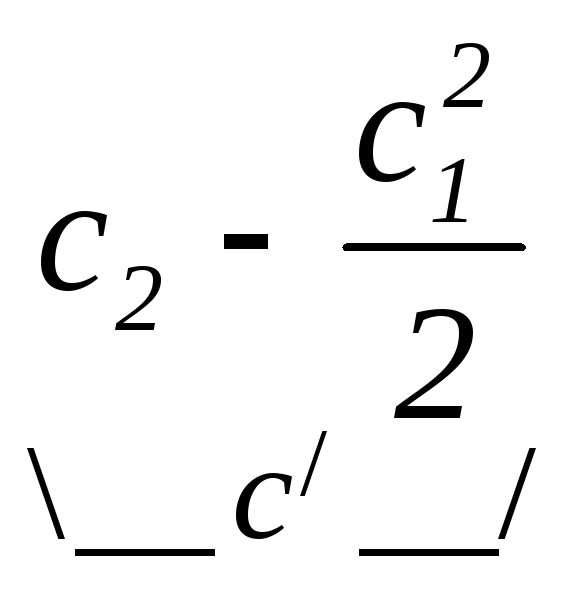Семейство фазовых траекторий имеет вид:
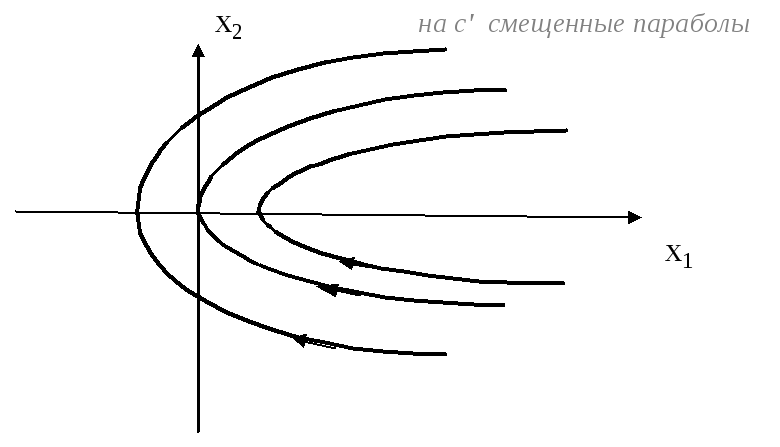
Фазовые
точки движутся снизу вверх, т.к.
=u
1,
>
0
* ускорение >0 скорость растет
2). u = -1
(t)
= -t +
(t)
= -
+
+
=
-
+
=
-
+
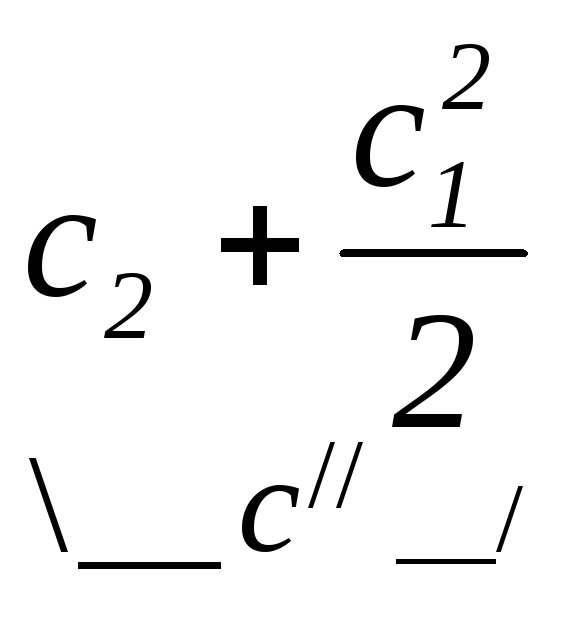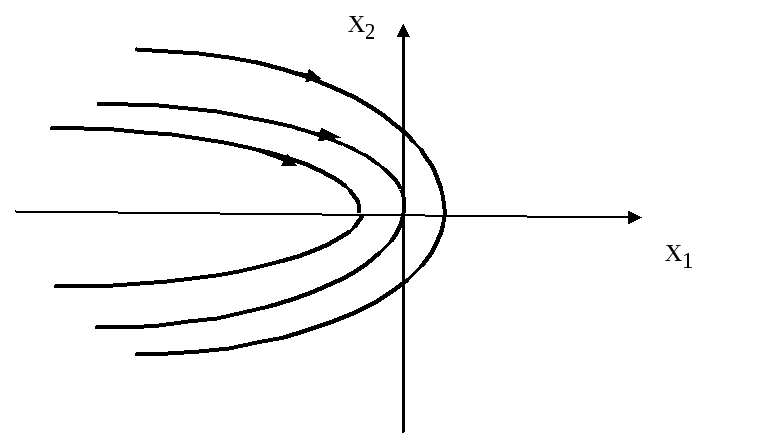
Фазовые точки движутся сверху вниз
* ускорение < 0 скорость падает
Общее семейство фазовых траекторий:
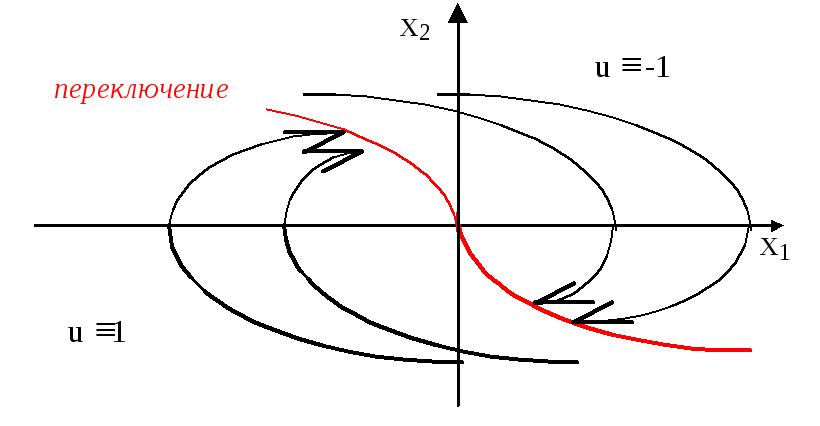
Таким образом. максимум одно переключение - траектория входит в ноль.
* мы должны перевести систему в ноль - см. начало
-
расстояние,
-
скорость
u = 1 - разгон (ускорение - производная скорости по времени > 0 )
u = -1 - торможение (ускорение < 0 ).
Согласно принципу максимума только изображенные траектории могут быть оптимальными, причем из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат , которая может быть оптимальной (т.е. задание начальной точки однозначно определяет соответствующую траекторию).
Можно доказать, что эти траектории оптимальны (т.е. обосновать достаточность).