2.2. Розподіл об’ємного заряду і поля в опз

2.2.1. Концентрації носіїв заряду

Електрофізичні властивості поверхні та приповерхневого шару напівпровідника визначаються величиною вигину зон на поверхні Y_s і в приповерхневій області Y(x), що залежить від електростатичного потенціалу поверхні _s та зміни його величини (x) в ОПЗ. Наявність у приповерхневій області внутрішнього електричного поля призводить до порушення у ній стану рівноваги між носіями заряду і кристалічною граткою. Зауважимо, що нерівноважні умови у цій області можуть зумовлюватися й іншими причиними, наприклад, збудженням носіїв заряду світлом, яке поглинається у тонкому приповерхневому шарі. Тому, як зазначено раніше, концентрації електронів і дірок в ОПЗ не збігаються зі значеннями n₀ і p₀ в об’ємі кристала за межею ОПЗ (n  n₀, р  p₀).

У теорії поверхневих властивостей напівпровідників концентрації носіїв заряду визначають через електростатичний потенціал  середини забороненої зони ( = – E_i/e) та потенціал , що відповідає рівню Фермі ( = – F/e).

У стані рівноваги положення рівня Фермі на поверхні _s і в об’ємі кристала ₀ повинні збігатися (_s = ₀). Величина ₀ однозначно пов’язана з концентраціями електронів n₀ і дірок p₀ за межами ОПЗ:

. (2.4)

де N_C і N_V – ефективні густини станів у с- та v-зоні відповідно, E_g – ширина забороненої зони напівпровідника.

Співвідношення (2.4) можна записати в іншому вигляді. Помножимо праву частину виразу для n₀ на величину exp[(₀ – ₀)], отримаємо:

. (2.5)

Як видно із (2.4), добуток n₀p₀ дорівнює:

. (2.6)

В об’ємі кристала величину E_g можна записати через потенціал ₀, що відповідає середині забороненої зони (рис. 2.2.):

. (2.7)

Підставивши (2.7) у (2.6), отримаємо:

. (2.8)

Тут n_і – концентрація носіїв заряду у власному напівпровіднику. При N_С = N_V із (2.8) отримаємо такий вираз для n_і:

. (2.9)

Враховуючи (2.9), вираз (2.5) можна записати у вигляді

. (2.10)

Аналогічно провівши перетворення виразу для концентрації дірок p₀, отримаємо:

(2.11)

Значення концентрації електронів і дірок в ОПЗ не можна визначати за допомогою рівноважного рівня Фермі ₀, оскільки у цій області немає рівноваги між носіями заряду і кристалічною граткою. Формально для визначення величин n i p у цьому випадку можна використати деякі співвідношення, подібні до виразів (2.10) і (2.11), якщо ввести квазірівні Фермі _n i _p для електронів і дірок відповідно, які не збігаються між собою (_n  _p). Тоді концентрації електронів і дірок в ОПЗ можна записати так:

, (2.12)

. (2.13)

Тут через  позначено потенціал, що відповідає середині забороненої зони напівпровідника в ОПЗ і тому значення  залежить від координати x (рис. 2.2). Це означає, що у цій області концентрації електронів і дірок залежать від x, тобто n=n(x), p=p(x). Тому можна вважати, що в ОПЗ наявні надлишкові концентрації носіїв заряду (Δn = n – n₀, Δp = p – p₀).

2.2.2.Залежність електростатичного потенціалу від координaт

Для визначення залежності електростатичного потенціалу від координати поблизу поверхні напівпровідника в стаціонарних умовах необхідно розв’язати рівняння Пуассона для одновимірного випадку:

, (2.14)

де (x) – густина об’ємного заряду в точці на відстані х від поверхні.

Розв’язок рівняння Пуассона проводять, використовуючи такі основні теоретичні припущення.

1. Розглядається невироджений напівпровідник, енергетичний розподіл носіїв заряду в якому, описується статистикою Максвела-Больцмана.

2. Вигин енергетичних зон не дуже сильний, так що в області поверхні напівпровідник також невироджений.

3. Домішкові центри в об’ємі напівпровідника вважаються повністю йонізованими.

4. Зміна потенціалу на віддалі, яка дорівнює довжині хвилі де-Бройля для електронів, значно менша, ніж 1 kT/e.

5. Зміна величини вигину зон Y_s від точки то точки поверхні є невеликою, що дозволяє охарактеризувати поверхню деякими одним усередненим значенням вигину зон.

Перераховані припущення в звичайних умовах виконуються для Ge і Si, але вони можуть не виконуватися для інших напівпровідників, що обмежує можливість використання теоретичних результатів при їх дослідженнях. Теорія поверхневих властивостей напівпровідників, яка базується на перерахованих припущеннях, розвинута в роботах Гаррета і Браттайна. Застосування цієї теорії при експериментальних дослідженнях та подальший її розвиток здійснені в роботах В.І. Ляшенка, А.В. Ржанова, О.В. Снітка, В.Г. Литовченка та ін.

При розв’язуванні рівняння (2.14) використовують такі граничні умови для напівнескінченного кристала:

(2.15)

Густина об’ємного заряду дорівнює:

(2.16)

де р(x), n(x) – концентрації дірок і електронів у точці x; N_d, N_a – концентрації донорів і акцепторів у напівпровіднику відповідно.

Розрахунок проводиться в загальному випадку для нерівноважних умов, коли концентрації вільних носіїв заряду в приповерхневій області задаються як термічною генерацією, так і іншими способами генерації, наприклад, освітленням поверхні світлом, яке сильно поглинається на поверхні.

В об’ємі кристала виконується умова електронейтральності

(2.17)

З урахуванням (2.17), вираз (2.16) набуває вигляду

(2.18)

Підставимо в (2.18) значення n₀, p₀, n i p, використовуючи вирази (2.10), (2.11), (2.12) і (2.13), отримаємо:

. (2.19)

Використовуючи вираз (2.19), рівняння (2.14) можна записати у вигляді:

. (2.20)

У правій частині рівняння (2.20) від х залежать , _p i _n. Величини _p i _n змінюються від _ps i _ns на поверхні (при x = 0) до ₀ на віддалі від поверхні порядку довжини дифузійного зміщення нерівноважних носіїв L_n,р. При невеликих відхиленнях від термодинамічної рівноваги (наприклад, при низьких рівнях збудження нерівноважних носіїв) та за умови, що товщина ОПЗ значно менша за L_n,р, градієнти _p i _n малі а отже, величини _p i _n можна вважати сталими в межах ОПЗ. Таке припущення виправдане для Ge і Si, для яких дифузійні довжини на декілька порядків більші від L.

Перший інтеграл рівняння Пуассона (2.20) легко взяти помноживши обидві його частини на та інтегруючи від x до , або від  до ₀, та враховуючи граничні умови :

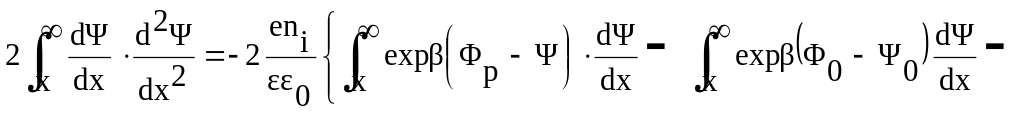
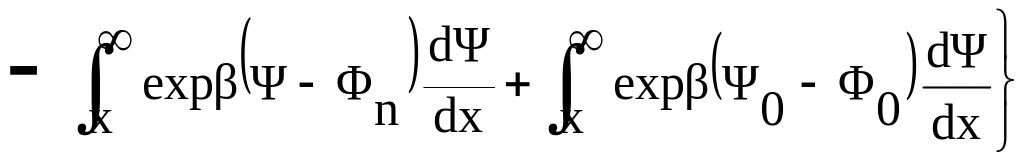, (2.21)

де .

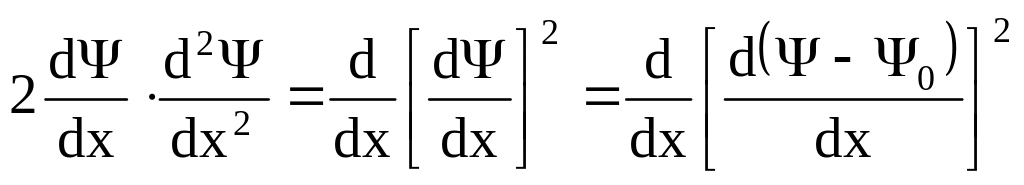У результаті інтегрування лівої частини даного рівняння одержимо:

.

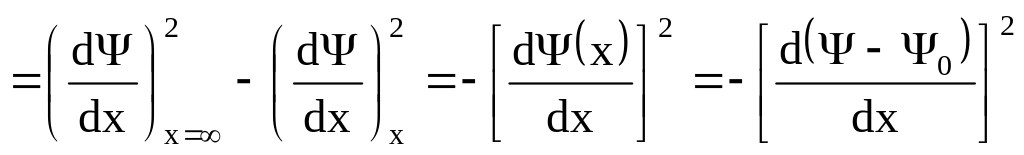Проінтегруємо праву частину рівняння (2.21):

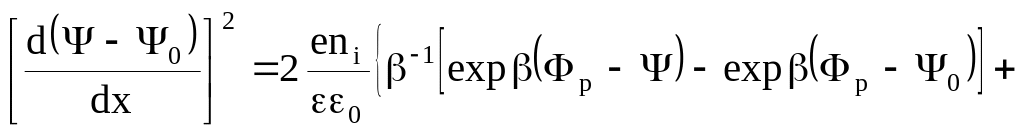
. (2.22)

Вираз (2.22) визначає потенціал для будь-якої точки області просторового заряду. Звичайно його записують у дещо простішому вигляді, який зручніший для аналізу. Для цього вводять такі безрозмірні величини:

, (2.23)

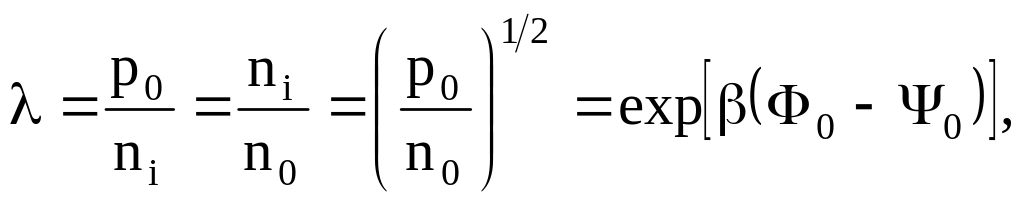(2.24)

(2.25)

Параметр λ характеризує об’ємне легування. Для кристалів легованих донорними домішками (n-тип) λ < 1, при легуванні акцепторними домішками (р-тип) λ > 1, а у напівпровіднику з власною провідністю λ=1. Як видно з наведеної на рис. 2.2. енергетичної діаграми величина визначається відстанню між рівнем Фермі та серединою забороненої зони в об’ємі кристала.

Використовуючи вирази (2.1) і (2.23) – (2.25), перший інтеграл рівняння Пуассона (2.22) можна записати у вигляді:

(2.26)

де

. (2.27)

Перший та другий доданки у виразі (2.27) визначаються внесками в об’ємний заряд вільних дірок та електронів відповідно, а третій – об’ємним зарядом нескомпенсованих домішок.

Із виразу (2.23) та наведеної на рис. 2.2. діаграми видно, що при вигині зон уверх, коли значення Y від’ємні, у приповерхневій області зосереджений позитивний об’ємний заряд Q_sc. У цьому випадку у виразі (2.27) береться знак “плюс”. При додатних значеннях Y, коли енергетичні зони вигнуті вниз і в приповерхневій області зосереджений негативний просторовий заряд, у виразі (2.27) береться знак “мінус”. Отже, при Y<0 у виразі (2.27) береться знак “плюс”, а при Y>0 – знак “мінус”.

Використовуючи вираз для першого інтеграла рівняння Пуассона можна визначити напруженість електричного поля Е_s на поверхні, об’ємний заряд у приповерхневій області Q_sc, а також заряд на вільній поверхні Q⁰_ss, який за величиною дорівнює заряду Q_sc, але протилежний за знаком (Q⁰_ss= – Q_sc). Напруженість електричного поля Е_s дорівнює

(2.28)

Зв’язок між Е_s та зарядом Q_sc в області просторового заряду за теоремою Остроградського-Гаусса визначається виразом

. (2.29)

Величину визначимо, використовуючи (2.23) та (2.26)

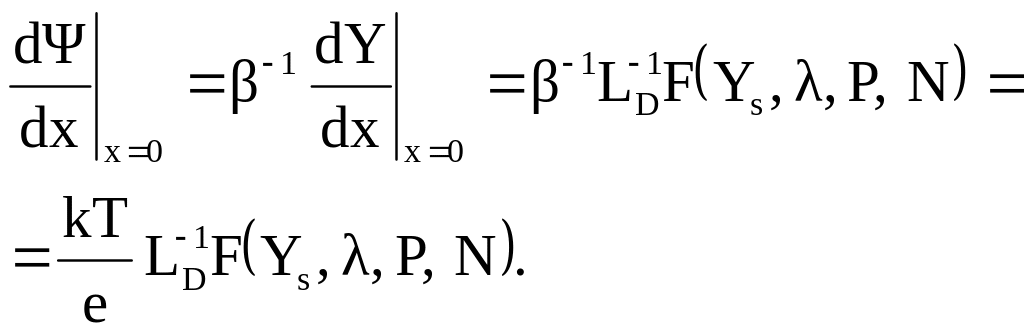(2.30)

Підставимо (2.30) у (2.29), отримаємо:

. (2.31)

Помножимо праву частину виразу (2.31) на величину і врахуємо (2.1)

(2.32)

Тут , де _s – значення електростатичного потенціалу, що відповідає середині забороненої зони на поверхні. Безрозмірна величина Y_s характеризує вигин зон у точці х = 0, тобто на поверхні кристала. Вона – важливий електрофізичний параметр поверхні.

Іноді в літературі для характеристики вигину зон використовують величину _s , яка показана на енергетичній діаграмі (рис. 2.2). Цю величину називають поверхневим потенціалом. На рис. 2.2 легко побачити, що величини _s  і Y_s зв’язані співвідношенням

. (2.33)

При теоретичних розрахунках залежності Q_sc, поверхневої провідності та інших величин від Y_s (чи _s) широко використовують рівноважний випадок, коли _n = _p = ₀ i P = N = 0. У цьому випадку, як випливає із (2.27), функція F залежить лише від Y_s та 

. (2.34)

Залежність електростатичного потенціалу  від координати х в ОПЗ у загальному випадку визначається другим інтегралом рівняння Пуассона.

Використовуючи вираз (2.26) другий інтеграл рівняння Пуассона можна записати у вигляді:

(2.35)

У загальному випадку через складність функції F(Y, , Р, N) хід потенціалу в ОПЗ можна обчислити лише за допомогою числового інтегрування. Але в ряді окремих часткових випадків можна одержати аналітичні вирази для описування форми приповерхневого потенціального бар’єра.