Управление и оптимизация / Novikov - Refleksiya i upravleniye 2013

Если при любых предпочтениях агентов r Î Ân сообщение ими достоверной информации является равновесием Нэша,

(2) " i N " r Î Ân " s Î Â1 fi(hi(r), ri) ³ fi(hi(r-i, s), ri),

то такой механизм называется неманипулируемым механизмом. Данное свойство далее будем называть неманипулируемостью.

Казалось бы, более сильным, чем (2), является требование того,

чтобы сообщение каждым агентом достоверной информации было его доминантной стратегией:

(3) " i Î N " ri, si Î 1 " s-i Î Ân-1 fi(hi(s-i, ri), ri) ³ fi(hi(s-i, si), ri).

Однако легко видеть, что определения (2) и (3) эквивалентны [207]. Это означает, что, так как в определениях (2) и (3) неманипу- лируемости механизмов планирования вектор r Î Ân типов агентов является «параметром», то неманипулируемость можно интерпрети- ровать следующим образом: механизм является неманипулируемым, если, каковы бы ни были истинные типы агентов, сообщение досто-

верной информации является доминантной стратегией каждого из них.

Рефлексивная неманипулируемость. Откажемся от предпо-

ложения о том, что вектор типов агентов является общим знанием, и

обобщим на этот случай задачу о неманипулируемости механизма планирования [122]. Пусть информированность i-го агента описыва- ется деревом Ii c элементами вида riσ Î Â1, σ Î S, причем ri – истин- ный тип i-го агента – достоверно ему известен, i Î N.

В этом случае агенты играют в рефлексивную игру, информаци- онное равновесие которой в данном случае определяется следующи- ми условиями (см. раздел 2.3):

1)структура информированности I имеет конечную сложность;

2)λ, μ Σ Iλi = Iμi Þ xλi* = xμi*;

3)" i Î N, " σ Î S

(4) s*	Arg max	f	(h (s*		,..., s*	, s	, s*	,..., s*	), r	) .
σi	si 1	i	i	σi1	σi,i −1	i	σi,i +1	σin	σi

В соответствии с (4) равновесное сообщение i-го агента (реаль- ного) зависит от структуры его информированности Ii, то есть

(5) si* = si* (Ii), i Î N.

161

Вчастном случае – если имеет место общее знание – выражение

(4)совпадает с определением равновесия Нэша.

Обозначим s*(I) = ( s1* (I1), s2* (I2), …,

маемое в соответствии с механизмом структуры информированности I:

sn* (In)). Решение x, прини- h(×), будет зависеть от всей

(6) x = h(s*(I)).

Обсудим теперь, что следует понимать под манипулируемостью в случае отсутствия общего знания.

Напомним, что в соответствии с (2) и (3) в условиях общего знания механизм является неманипулируемым, если, каковы бы ни были истинные типы агентов, сообщение достоверной информации является доминантной стратегией каждого агента.

Попробуем обобщить это определение на случай информацион- ного равновесия – потребуем, чтобы какова бы ни была структура информированности реального агента, сообщение достоверной

информации являлось бы для него компонентой информационного равновесия (4):

(7) r n, i N, Ii

ri Arg max

f

(h

(s*

(I

),..., s*

(I

), s

, s*

(I

),..., s*

(I

)), r ) .

si 1

i

i

i1

i

i,i−1

i

i

i,i+1

i

in

i

i

Легко видеть, что, если выполнено (3) (механизм является не- манипулируемым), то имеет место и (7). В другую сторону: так как

множество всевозможных структур информированности включает и структуру, соответствующую общему знанию, то, если выполнено (7), то механизм является неманипулируемым (должно иметь место (3)). Получили, что определения (3) и (7) эквивалентны.

Итак, можно сделать следующий качественный вывод: если в

рассматриваемом механизме у каждого агента при любом его типе существует доминантная стратегия (а это – очень сильное требова- ние, и класс удовлетворяющих ему механизмов чрезвычайно узок), то принимаемые им решения не зависят от структуры информиро- ванности.

Ослабления требования неманипулируемости можно добиться, введя определение рефлексивной неманипулируемости – существо- вания подструктур информированности riσ 1, i N, s Σ+, та-

162

ких, что при любых типах реальных агентов сообщение ими досто- верной информации является информационным равновесием.

Формально: будем называть механизм h(×) рефлексивно немани-

пулируемым, если существуют подструктуры информированности riσ Î Â1, s Î S+ , реальных агентов (i Î N), такие, что, каков бы ни был тип реального агента, сообщение достоверной информации является для него компонентой информационного равновесия:

(9)	" i Î N " ri Î Â1
	ri Î Arg max f		(h (s*	,..., s*	, s	, s*	,..., s*	), r ) ,
	si 1	i	i i1	i,i −1	i	i,i +1	in	i
(10)	" s Î S " j Î N

s*	Arg max f		(h	(s*	,..., s*	, s		, s*	,..., s*	), r	) .
iσj	s j 1	j	j	iσj1	iσj, j−1		j	iσj, j+1	iσjn	iσj

Понятно, что множество рефлексивно неманипулируемых меха- низмов не уже множества неманипулируемых механизмов (любой неманипулируемый механизм является рефлексивно неманипули- руемым), поэтому их характеризация (в том числе – поиск соответ- ствующих подструктур информированности) является актуальной задачей.

Обозначим EI – множество всевозможных (при всех допустимых структурах информированности) равновесных наборов действий реальных агентов, E-i = Proj-i EI, i Î N. Определение (9)–(10) можно сформулировать в следующем виде: механизм является рефлексивно неманипулируемым, если для i-го агента существует обстановка ~r−i Î E-i, такая, что:

~	Î Â	1	~	~	,	~	), ri), i Î N.
(11) " ri, ri			fi(hi( r−i	, ri), ri) ³ fi(hi( r−i		ri

Обозначим множество равновесий Нэша

(12)EN = {r Î Ân |" i Î N " ~ri Î Â1 fi(hi(r), ri) ³ fi(hi(r-i, ~ri ), ri)},

(13)X i0 = Proji EN, i Î N.

Далее до конца данного раздела будем предполагать, что струк- тура информированности агентов является конечной регулярной.

Справедливо следующее утверждение – достаточное условие рефлексивной неманипулируемости (необходимым условием явля-

ется (11)).

163

~r = ( ~r1 ,

Утверждение 2.16.1. Для того чтобы механизм планирования являлся рефлексивно неманипулируемым, достаточно, чтобы для любого i-го агента, i N, существовал набор типов

…, ~rn ) EN такой, что выполнено (11). При этом для построения

рефлексивно неманипулируемых механизмов достаточно ограни- читься рассмотрением агентов с не более чем вторым рангом реф- лексии.

Доказательство. Достаточно сформировать структуру информи- рованности i-го агента Ii (отметим, что структуры информированно- сти различных агентов можно строить независимо) такую, что:

(14) rijσk = ~rk , j ¹ i, для любого s Σ.

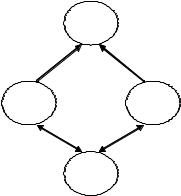
Это означает, что с точки зрения i-го агента все остальные счи- тают, что имеет место общее знание (см. Рис. 42).

Легко видеть, что с точки зрения i-го агента сообщение досто-

верной информации является равновесием игры его фантомных агентов, следовательно, выполнено (10), что с учетом (11) приводит к выполнению (9). ∙

i

ij ik

iji

Рис. 42. Граф рефлексивной игры с точки зрения i-го агента

Содержательно, представления i-го агента о типах оппонентов и их представлениях должны быть следующими. Агент должен быть, во-первых, уверен, что типы оппонентов таковы, что выполнено условие (11), обеспечивающее выгодность сообщения ими достовер- ной информации. Во-вторых, представления оппонентов с точки

164

зрения рассматриваемого агента должны быть таковы, что сообще- ние именно данной информации является равновесием их игры (см. условие (10)). Для этого достаточно, чтобы на нижнем уровне струк-

туры информированности имело место субъективное общее знание фантомных агентов.

Отметим конструктивность приведенного доказательства – оно содержит алгоритм построения конкретной структуры информиро- ванности (14), обеспечивающей рефлексивную неманипулируе- мость.

Приведем пример механизма планирования, который является манипулируемым, но при этом рефлексивно неманипулируемым.

Пример 2.16.1. Пусть имеются два агента с неотрицательными типами r1 и r2. (Напомним, что типом агента в данном случае являет- ся оптимальный для него план.) Рассмотрим механизм, который в зависимости от сообщений агентов s1 и s2 назначает им планы x1 и x2 соответственно по следующим формулам:

(15) x1 = s1 – s2 / 2, x2 = s2 – s1 / 2, s1, s2 ³ 0.

Решая систему уравнений

ìïs1 - s22 = r1,

í

ïïs2 - s1 = r2 , î 2

получаем равновесные по Нэшу стратегии (заявки) агентов:

s* (r1, r2) =	2	(2 r1 + r2),	s* (r1, r2) =	2	(2 r2 + r1).
1	3		2	3

Легко видеть, что механизм (15) является манипулируемым – при любых типах агентов, не равных одновременно нулю, по край- ней мере один из агентов сообщает заявку, не совпадающую с его типом. Однако при r1, r2 ³ 0 механизм является рефлексивно нема- нипулируемым. Действительно, достаточно убедить каждого агента в том, что с точки зрения его оппонента общим знанием является равенство нулю обоих типов. Иными словами, достаточно сформи- ровать структуру информированности riσ= 0, i =1, 2, σ Î S+ . Тогда

единственным информационным равновесием является набор si* = ri, si*σ = 0, i =1, 2, σ Î S+ .

Таким образом, в равновесии оба агента сообщают свои истин- ные типы.

165

В то же время, при r1, r2 > 0 механизм (15) не является рефлек- сивно неманипулируемым, так как какова бы ни была структура информированности (и, в частности, какова бы ни была ее глубина), каждый из агентов будет уверен в том, что сообщение оппонента будет отлично от нуля. ∙

Ряд прикладных механизмов планирования исследован (с точки

зрения стабильности взаимных представлений агентов о типах друг друга, при которых механизм обладает теми же свойствами) в [7, 32, 33, 85, 116 и др.].

166

ГЛАВА 3. СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ

ИУПРАВЛЕНИЕ

Внастоящей главе исследуются модели стратегической рефлек- сии. В разделе 3.1 рассматривается модель стратегической рефлек- сии в игре двух лиц, что в разделе 3.2 позволяет решить задачу о

максимальном целесообразном ранге стратегической рефлексии в

биматричных играх, а также определить и изучить т.н. игры рангов. Раздел 3.3 посвящен обсуждению конечности ранга рефлексии, порождаемой ограниченностью способностей человека по перера- ботке информации. Раздел 3.4 – описанию метода рефлексивных разбиений, используемого для решения задач рефлексивного управ-

ления.

3.1. СТРАТЕГИЧЕСКАЯ РЕФЛЕКСИЯ В ИГРАХ ДВУХ ЛИЦ

Рассмотрим последовательно, в порядке возрастания информи- рованности, рефлексивные модели принятия решений в играх двух лиц.

Нулевой ранг рефлексии. Проанализируем задачу принятия агентом решения в случае полного отсутствия информации о со- стоянии природы (напомним, что предположение о том, что целевые функции и допустимые множества являются общим знанием, счита- ется выполненным). Представляется разумным, с одной стороны, принцип принятия решений на основе максимального гарантирован- ного результата, в соответствии с которым i-ый агент выберет гаран- тирующую (по состоянию природы и действию оппонента) страте-

гию

(1)	1	xг	= arg max min	min fi(θ, xi, x-i).
		i	xi X i θ Θ	x−i X −i

С другой стороны, гипотетически принцип (1) принятия реше- ний не является единственно возможным – агент может рассчиты- вать, что его оппонент выберет не наихудшее действие, а собствен- ную гарантирующую стратегию (отметим, что каждый агент может вычислить гарантирующую стратегию оппонента). Тогда наилуч-

шим ответом будет

(2)	2	xг	= arg max min fi(θ, xi,	1	xг	).
		i	xi X i θ Θ		−i

Но аналогичным образом может рассуждать оппонент рассмат- риваемого агента. Если рассматриваемый агент допускает такую возможность, тогда его гарантирующей стратегией будет

(3)	3	xг	= arg max min fi(θ, xi,	2	xг	),
		i	xi X i θ Θ		−i

где 2 x−гi вычисляется в соответствии с (2) заменой индекса «i» на «-

i» и наоборот. Цепочку наращивания «ранга рефлексии» (предполо- жений агента о ранге рефлексии оппонента) можно продолжать и далее (см. аналогии в динамических моделях, рассматриваемых в [126]), определив рекуррентно

(4)	k	xг	= arg max min fi(θ, xi,	k −1	xг	), k = 2, 3, ...,
		i	xi X i θ Θ		−i

где 1 xiг , i = 1, 2, определяются (1). Набор действий типа (4) будем

называть множеством рефлексивных гарантирующих стратегий.

Рассмотрим иллюстративный пример.

Пример 3.1.1. Пусть целевые функции агентов имеют вид: f1(x1, x2) = x1 – x12 /2x2, f2(x1, x2) = x2 – x22 /2(x1 + δ),

где δ > 0. Относительно допустимых множеств предположим, что X1 = X2 = [ε; 1], 0 < ε < 1. Будем считать, что каждая из констант ε и δ много меньше единицы. Гарантирующие стратегии агентов приве- дены в Табл. 4.

Видно, что, во-первых, значения гарантирующих действий уве- личиваются с ростом «ранга рефлексии». Во-вторых, различным «рангам рефлексии» агентов соответствуют в общем случае различ- ные гарантирующие действия (отметим, что равновесием34 Нэша в данном примере является вектор (1; 1)). ∙

Табл. 4. Гарантирующие стратегии агентов в примере 3.1.1

k	1	2	3	4	5	6	7	...
k x1г	ε	ε + δ	ε + δ	ε + 2δ	ε + 2δ	ε + 3δ	ε + 3δ	...
k x2г	ε + δ	ε + δ	ε + 2δ	ε + 2δ	ε + 3δ	ε + 3δ	ε + 4δ	...

34 В качестве отступления заметим, что, если в рассматриваемом примере целевая функция второго агента имеет вид f2(x1, x2) = x2 + x22 /2x1, то у него существует доминантная стратегия (равная единице), и последовательность гарантирующих стратегий первого агента стабилизируется уже на втором члене: 1 xiг = ε, 2 xiг = 1/2. Если первый агент может вычислить доминантную стратегию своего оппонента, то представляется рациональным выбор им действия 2 xiг .

168

Вопрос о том, какое действие следует выбирать агенту, остается открытым. Единственно, можно констатировать, что, обладая ин-

формацией только о множестве возможных значений состояния природы, i-ый агент может выбирать одно из действий k xiг , i = 1, 2;

k = 1, 2, ..., определяемых выражениями (1)-(4).

Доопределить рациональный выбор агента в рассматриваемой модели можно следующим образом. Если агенту неизвестна целевая функция оппонента (что исключено в рамках предположения о том,

что целевые функции и допустимые множества являются общим знанием), то единственным его рациональным действием является выбор (1), то есть классический МГР. В рамках введенных предпо- ложений агенту известна целевая функция оппонента, а также из- вестно, что оппоненту известен этот факт и т.д. Поэтому с точки зрения агента нерационально использование классического МГР, и ему следует рассчитывать, как минимум, что оппонент будет ис-

пользовать МГР, что приведет к выбору 2 xiг . Но, опять же, в силу

того, что целевые функции являются общим знанием, агент может предположить, что такой ход его рассуждений может быть восста-

новлен оппонентом, что сделает целесообразным выбор 3 xiг и т.д. до

бесконечности. Следовательно, с точки зрения агента остается неоп- ределенность относительно «ранга рефлексии» оппонента35. Относи- тельно этого параметра он не имеет никакой информации (если у агента имеются некоторые убеждения по этому поводу, то может реализоваться соответствующее субъективное равновесие), что

делает рациональным использование гарантированного результата по «рангу рефлексии» оппонента:

(5) x’i = arg max	min	min fi(θ, xi,	j x−гi ).
xi X i	j =1,2,...	θ Θ

35 Другими словами, исходная игра может быть заменена на игру, в которой агенты выбирают ранги своей рефлексии. Для новой игры могут быть также построены рефлексивные аналоги и т.д. до бесконечности (см. примеры: «Пенальти» – во введении, «Игра в прятки» и «Снос на мизере» – в разделе 3.2). Одним из возмож- ных способов борьбы с подобной «бесконечностью» является использование гарантированного результата по рангу рефлексии оппонента. Другим возможным способом, эффективным для конечных игр, является определение максимального целесообразного ранга рефлексии агентов – см. раздел 3.2.

169

Отметим, что, во-первых, x’i может отличаться от классической гарантирующей стратегии 1 xiг , определяемой выражением (1). Во-

вторых, при использовании стратегии (5) факт наличия доминантной стратегии оппонента будет учтен агентом (см. сноску в примере

3.1.1).

ВТабл. 5 приведены значения целевой функции первого агента

впримере 3.1.1 в зависимости от «ранга рефлексии» оппонента и соответствующие действия оппонента. Видно, что при использова-

нии стратегии (5) выигрыш i-го агента равен ε + δ, что превышает выигрыш ε, получаемый при использовании классического МГР.

Табл. 5. Выигрыши первого агента в примере 3.1.1

j	1	2	3	4	5	6	7
2 f1(BR1( j x2г ), j x2г )	ε + δ	ε + δ	ε + 2δ	ε + 2δ	ε + 3δ	ε + 3δ	ε + 4δ
j x2г	ε + δ	ε + δ	ε + 2δ	ε + 2δ	ε + 3δ	ε + 3δ	ε + 4δ

Таким образом, рациональным в рассматриваемой модели мож- но считать использование агентом стратегии (4) или (5).

Первый ранг рефлексии. Предположим теперь, что агент об- ладает определенной информацией о состоянии природы, которую считает истинной, и больше ему ничего достоверно не известно.

В рамках существующей неопределенности в силу принципа де- терминизма у агента, осуществляющего стратегическую рефлексию, имеются две альтернативы – либо предположить, что его оппонент не обладает никакой информацией, либо считать, что последний обладает той же информацией, что и он сам36.

Если агент не вводит никаких предположений об информиро- ванности и принципах поведения оппонента, то он вынужден при- менять принцип максимального гарантированного результата (МГР)

– никакой дополнительной (по сравнению с рассмотренной выше моделью нулевого ранга рефлексии) информации об оппоненте у

36 Данный принцип (и его обобщения) будет широко использоваться ниже при определении конечных информационных структур – действительно, обладая ин- формацией Ii, i-ый агент может в случае неопределенности приписывать другим агентам только информированность, согласованную с Ii.

170