8.3. Приклади обчислення математичного сподівання двв.

1. Біномний розподіл ДВВ.

Теорема 1. Математичне сподівання М(Х) числа появи події А в п незалежних випробуваннях дорівнює добутку числа випробувань п на ймовірність р (0 < р < 1) появи події А в кожному випробуванні:

М(Х) = пр. (10)

Доведення.

Приклад 4. Ймовірність влучення в ціль при стрільбі гармати

дорівнює р = 0,6 . Знайти математичне сподівання М( X) загального числа влучень, якщо зроблено 10 пострілів.

Розв'язання. М ( X) = пр = 10 ∙ 0,6 = 6 (влучень).

2. Геометричний розподіл ДВВ.

Теорема 2. Якщо ДВВ X мас геометричний розподіл, то її

математичне сподівання М(Х) = ¹/_p , де р (0 < р < 1) - ймовірність

появи події в одному випробуванні.

Доведення. За умовою теореми ДВВ має геометричний розподіл,

тому P(X=k) = q^k-1 p, (k = 1,∞). Тоді

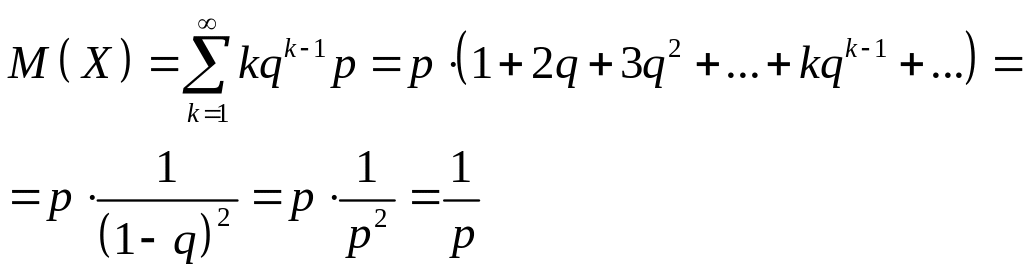
Пояснення. При 0 < q < 1 степеневий ряд 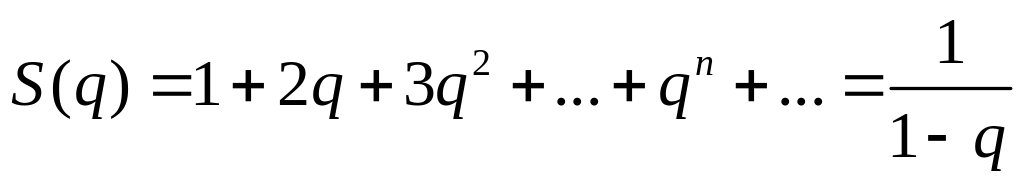можна почленно диференціювати, і сума одержаного ряду дорівнює похідній від суми ряду, тобто

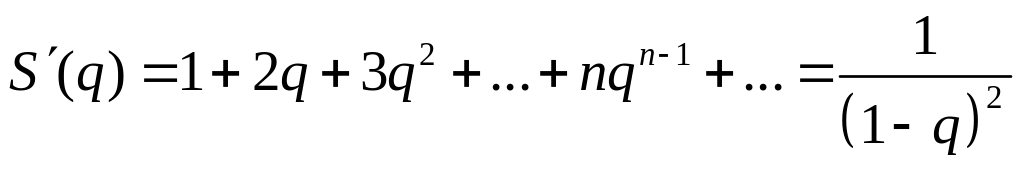
3. Розподіл Пуассона.

Теорема 3. Якщо ДВВ X має розподіл Пуассона з параметром А,

то її математичне сподівання М(Х) =λ

Доведення За умовою Д ВВ мас розподіл Пуассона з параметром λ, тому 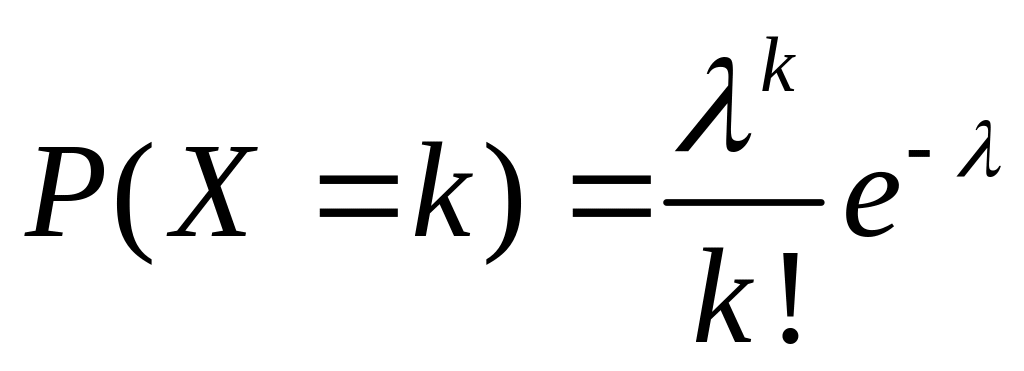(k = 0,∞). Отже,

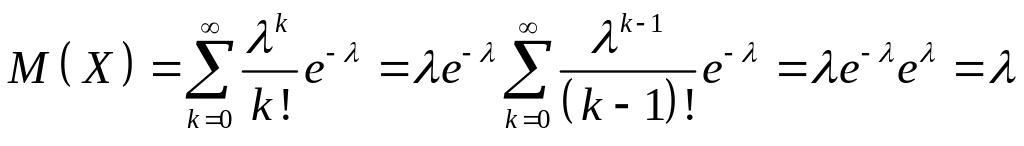
8.4. Відхилення випадкової величини від її математичного сподівання.

Математичне сподівання не дає повної характеристики випадкової величини, наприклад, не показує ніякі значення вона приймає, ні як вона розміщена навколо свого середнього значення. Розглянемо приклад.

Y	-100	100
Р	1 2	1 2

Приклад 5. Дві випадкові величини X та Y задано розподілами

X	-0,01	0,01
р	1 2	1 2

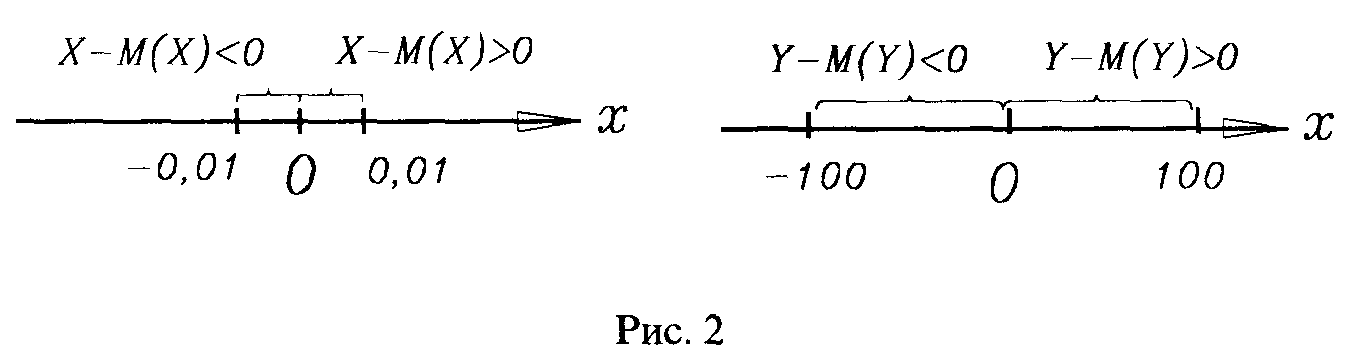
Знайдемо М(Х) і М(Y):

.

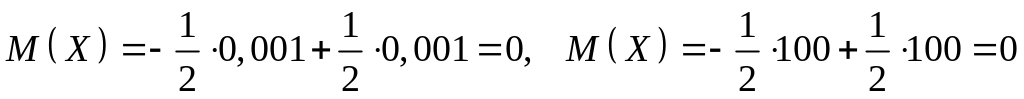Отже, математичні сподівання М( X) і М( Y) однакові, хоча значення X і Y суттєво відрізняються одне від одного, а в другому випадку і від .М(Y).

Введемо нову величину, що характеризує відхилення випадкової величини X від M( X).

Означення 5. Відхилення випадкової велечини X називається різниця між випадковою велечиною та її математичним сподіванням.

тобто X — М( X).

Теорема 4. Математичне сподівання відхилення випадкової величини від свого математичного сподівання дорівнює нулю:

M(X - M(X)) = 0.

Дійсно, згідно з властивостями М(Х) маємо.

M(X - M(X))= M(X) -M(M(X))= M(X) - M(X) = 0.

Отже, введена величина теж недостатньо характеризує розміщення значень Д ВВ. Тому в теорії ймовірностей розглядається квадрат відхилення

ДВВ.

Запитання для самоконтролю.

1. Що таке математичне сподівання ДВВ? Який ймовірнісний та механічний зміст математичного сподівання?

2. Назвіть та доведіть основні властивості математичного сподівання ДВВ.

3. Обчисліть математичне сподівання ДВВ, розподіленої за біномним законом.

4. Обчисліть математичне сподівання ДВВ, розподіленої геометрично.

5. Обчисліть математичне сподівання ДВВ, розподіленої за законом Пуассона.

6) Що таке відхилення ДВВ від її математичного сподівання? Чому дорівнює його математичне сподівання?