Структура лекції

1. Вступна частина:

   1. Оголошення теми, мети і завдань лекції.

   2. Ознайомлення з планом лекції, основною та додатковою літературою.

2. Виклад лекційного матеріалу (згідно плану та вимог до лекції).

І. Кортеж. Поняття пари.

Слово «кортеж» зустрічається в нашому житті. «Весільний кортеж» - це множина машин, що їдуть у певному порядку. Такі об’єкти як номера телефонів, машин, будинків, слова із певного числа букв охарактеризувати терміном «множина» не завжди можна, бо, по-перше, в номерах чи словах важливий порядок цифр (букв), а для множини порядок елементів не відіграє ролі, по-друге, в номерах або у словах цифри (букви) можуть повторюватися, у множинах кожен елемент входить один. Тому ввели нове поняття, яке відрізнялось від поняття множини. Це – кортеж або «розміщення». Семизначні номери телефонів Києва – це кортежі, букви в словах – це кортежі певної довжини.

Означення. Кортежем довжини k називається упорядкований набір k елементів, з яких деякі можуть бути і однаковими.

Два кортежі вважаються рівними тоді і тільки тоді, коли вони мають однакову довжину і на відповідних місцях у них стоять однакові елементи.

Пара – це кортеж довжини 2. (Н.: усі можливі кортежі довжини 2 із цифр 1, 2, 3 мають вигляд: (1, 1); (2, 2); (3, 3); (1, 2); (1, 3); (2, 1); (2, 3); (3, 1); (3, 2).

В початкових класах діти виконують задачу «Використовуючи цифри 1, 2, 3, утворити всі можливі двозначні числа». Шляхом підбору діти отримують:

11 12 13

21 22 23

31 32 33

Запис кожного отриманого числа складається з двох цифр, причому існує порядок їх слідування: наприклад, із цифр 1 та 2 утворено два різні числа 12 та 21.

У тому випадку, коли важливий порядок слідування елементів множини, в математиці говорять про впорядкований набір елементів. У даній задачі ми маємо справу з упорядкованими парами.

Упорядковану пару, утворену з елементів a та b, прийнято позначати (a, b), причому елемент a називають першою координатою (компонентою) пари, а елемент b – другою координатою (компонентою) цієї пари.

Пари (a, b) та (c, d) рівні тільки в тому випадку, якщо а = с та b = d.

В упорядкованій парі може бути, що a=b. Так, числа 11, 22, 33, можливо розглядати як упорядковані пари (1, 1), (2, 2), (3, 3).

ІІ. Декартовий добуток множин.

У процесі виконання цієї задачі із двох даних множин А та В утворено нову множну, елементи якої являються упорядковані пари чисел. Цю нову множину називають декартовим добутком множин А та В.

Означення. Прямим або Декартовим добутком множин А та В називається множина, елементами якої є усі упорядковані пари (а, b), в яких перша компонента належить множині А, а друга компонента належить множині В.

Декартів добуток множин А та В позначається АВ.

Операцію, за допомогою якої знаходять декартів добуток, називають декартовим множенням множин.

Декартів добуток не володіє переставною властивістю, тобто існують такі множини А та В, що АВВА.

Наприклад: множин: А = {1, 2, 3}, n (А) = 3

В = {а, с}, n (В) = 2.

Декартові добутки АВ = {(1, а); (1, с); (2, а); (2, с); (3, а), (3, с)},

n (АВ) = n (А)  n (В) = 23 = 6.

Декартів добуток множин не підчиняється комутативному і сполучному законам, але пов’язана з операцією об’єднання множин розподільною властивістю: для будь-яких множин А, В та С має місце рівність (АВ)С=(АС)(ВС).

Елементи декартового добутку двох скінчених множин зручно записувати за допомогою прямокутної таблиці. Наприклад, декартовим добуток множин А={1, 2, 3} та В={3, 5} можна представити у вигляді таблиці:

В А	3	5
1	(1, 3)	(1, 5)
2	(2, 3)	(2, 5)
3	(3, 3)	(3, 5)

У математиці розглядають не тільки впорядковані пари, але і впорядковані набори із трьох, чотирьох тощо елементів. Такі впорядковані набори називають ще кортежами. Так, (1, 5, 6) – кортеж довжини 3 (тобто в ньому три елементи), а (7, 8, 9, 4, 3) – кортеж довжини 5.

Використовуючи поняття кортежу, можна визначити поняття декартового добутку n множин.

Означення. Декартовим добутком множин А₁, А₂, …, А_n називається множина кортежів довжин n, утворених так, що перша компонента кортежу належить множині А₁, …, n-я – множині А_n .

Позначають декартів добуток множин А₁, А₂, …, А_n так: А₁А₂ …А_n.

Знайдемо декартовим добуток множин А₁, А₂, А₃, якщо А₁={2, 3}, А₂={3, 4, 5}, А₃={7, 8}.

Елементами декартового добутку А₁А₂А₃ будуть кортежі довжини 3, утворені так: перша компонента буде вибиратися із множини А₁, друга – із множини А₂, третя – із множини А₃. В результаті отримаємо: А₁ А₂А₃= {(2,3,7), (2,3,8), (2,4,7), (2,4,8), (2,5,7), (2,5,8), (3,3,7), (3,3,8), (3,4,7),(3,4,8), (3,5,7), (3,5,8)}

ІІІ. Поняття універсальної множини.

Ми розглядали приклади, де певна множина була найбільша, а інші розглядались, як її підмножини. Множина студентів у коледжі, множина трикутників, дійсних чисел – це приклади універсальних множин. Позначають вони I або U.

Н.: І – множина трикутників, А – множина рівнобедрених трикутників, В – множина рівносторонніх трикутників, С – множина гострокутних трикутників.

А І, В І, С І.

ІV. Доповнення підмножини.

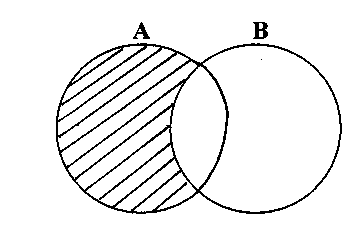
Означення. Доповнення множини А і В називається множина, яка містить тільки ті елементи множини А, які не належать множині В.

А\В

Якщо хА\В  хА, хВ

Н.: А={1, 2, 3, 5}, В={1, 5}, то А\В={2,3}

Операція, за допомогою якої знаходять доповнення підмножини називається різницею множин.

Означення. Різницею множин А і В називається множина, яка містить у собі усі елементи, що належать множині а і не належать множині В. Позначається А\В.

V. Поняття розбиття множин на підмножини, які попарно не перетинаються (на класи).

Поняття множини і операцій над множинами дозволяє нам уточнити наше уявлення про класифікацію.

Класифікація – це, дія, розподіл об’єктів по класам на основі схожості об’єктів всередині класу і відмінності їх від об’єктів інших класів.

Як правило, метою класифікації являється систематизація наших знань. Н.: у біології класифікація охоплює більше 1,5 млн. тварин. Класифікація дає можливість розглянути цю багатогранність в певній системі, виділить цікаві для нас види рослин чи тварин.

Широко використається класифікація в математиці.

Н.: натуральні числа діляться на парні та непарні; кути – гострі, прямі і тупі.

Будь-яка класифікація пов’язана з розподілом деякої множини на підмножини.

Вважають, що множина Х розбита на класи Х₁, Х₂, …Х_n, якщо:

1. Підмножини х1, х2, …Хn попарно на перетинаються.

2. Об’єднання підмножин х1, х2, …Хn співпадає з множиною х.

3. Підмножини не порожні.

Якщо не виконана хоча б одна з умов, класифікації вважають неправильною.

Н.: множину Х трикутників можна розбити на три класи: трикутники з гострими кутами, прямокутні, тупокутні. Дійсно, виділені підмножини попарно на перетинаються та їх об’єднання співпадає з множиною Х.

Однак, не всяка система підмножин даної множини представляє собою розбиття цієї множини.

Н.: якщо з множини Х трикутників виділити підмножини рівнобедрених, рівносторонніх і різносторонніх, то розбиття множини Х на класи ми не отримаємо, оскільки множина рівнобедрених та рівносторонніх трикутників перетинаються (всі рівносторонні трикутники являються рівнобедреними).

Отже, класифікація пов’язана з виділенням із множини його підмножин. Але, щоб виділити підмножину, достатньо вказати характеристичну властивість його елементів.

Розглянемо, наприклад, множину натуральних чисел. Її елементи мають різні властивості. Серед натуральних чисел є парні, непарні, кратні 3, кратні 5 тощо. Представимо, що нас цікавлять натуральні числа, які мають властивість – діляться на 3. Ця властивість дозволяє виділити із множини натуральних чисел підмножину чисел, кратних 3. Тоді, про останні натуральні числа можна сказати, що вони не кратні 3, тобто, отримуємо ще одну підмножину множини натуральних чисел.

Виділені множини не перетинаються, а їх об’єднання співпадає з множиною N натуральних чисел.

Таким чином, задання однієї властивості елементів множини натуральних чисел привело до розбиття цієї множини на два класи: клас чисел кратних 3 (його представниками являються, наприклад, 3, 6, 15), та клас чисел не кратних 3 (4, 5, 13).

Розбиття множин на класи за допомогою двох властивостей, тобто виділення із множини дві різних підмножини.

Розглянемо дві властивості натуральних чисел: «бути кратним 3» та «бути кратним 5». За допомогою цих властивостей із множини натуральних чисел можна виділити дві підмножини: А – підмножина чисел, кратних 3, і В – підмножина чисел, кратних 5. Ці підмножини перетинаються, але не один із них не є підмножиною другого.

Круг, який зображує множину N натуральних чисел, розбився на 4 не перетинаючись області. Кожна область зображує деяку підмножину множини N. Визначимо, які числа отримались у кожному із цих неперетинаючихся підмножин. Підмножина І – складається із чисел, кратних 3 і 5, підмножина ІІ – із чисел, кратних 3 та не кратних 5, ІІІ – із чисел, кратних 5 та не кратних 3, ІV - із чисел не кратних 3 та не кратних 5. Об’єднання цих чотирьох підмножин є множина N.

Отже, виділення двох властивостей натуральних чисел привело до розбиття множини натуральних чисел на 4 класи.

Але не слід думати, що задання двох властивостей елементів множини приводить до розбиття цієї множини саме на 4 класи. Так буває не завжди.

Н.: при допомозі двох властивостей «бути прямокутником» та «бути тупокутником» множина трикутників розбивається на 3 класи.

- клас прямокутних трикутників

- клас тупокутних трикутників

- клас трикутників, які не являються ні прямокутними, ні тупокутними трикутниками.

3. Заключна частина:

   1. 3.1. Загальний висновок.

   2. 3.2. Відповіді на запитання студентів.

   3. 3.3. Д/з: Стойлова Л.П., Пишкало А.М. Основы начального курса математики, п. 31 – 35, впр. 4 (C. 90).