The system of normal equations (6.76) has a solution X

given by

X = n""^"U = (A^TPA) ~¹ (A^TPL) (6.77)

T

if the normal equation matrix, N = A PA, has an inverse. Note that N is a symmetric positive definite matrix.²)

To discuss the influence of the weight matrix P on the solution vector X, let us use a different weight matrix, say P', such that

P' = yP (6.78)

where у is an arbitrary constant. Substituting (6.78) into (6.77) we get:

T -1 T X¹ = (A P'A) (A P'L)

= (а^ура)""¹ (A^TyPL) (6.79)

1 T -1 T -= - (A PA) у (A PL) Y

= X .

This result indicates that the factor к in equation (6.66) for computing the weight matrix P from can be chosen arbitrarily without any influ-ence on X, which really verifies the statement we have made earlier, in section 6.4.4.

It should be noted that the vector of discrepancies V as defined in (6.70), becomes after minimization of the vector of residuals (see 4.8) of the observed quantities. As such, it should be again denoted by a different symbol, say R, to show that it is no longer a vector of variables (function of X) but a vector of fixed quantities. Some authors use v for this purpose and this is the convention we are going to use (see also 6.4.2) . The values v^ are computed directly from equation (6.70) in the same units as these of the vector L. Then the adjusted observations will be given by L = L + V.

We should keep in mind that one of the main features of the parametric method of adjustment is that the estimate of the vector of unknown parameters, i.e. X, is a direct result of this adjustment as given by equation (6.77).

At this stage, it is worthwhile going back to the trivial

problem of adjustment - the sample mean. According to the equation (6.79),

we can choose the weights of the individual observations to be inversely

proportional to their respective variances with an arbitrary constant к

of proportionality. This indicates that the weights do not have to equal

n

to the experimental probabilities for which £ P. =1, as we required

i=l ¹

In sections 6.4.2 and 6.4.3. In this case, the observation equations will be

x = + v^, with weight p^,

Л, mm /4

x = &₂ + ^v2' with weight p₂,

x = I 4- v , with weight P . n n n

Or, in matrix form

AX = L + V ,

where

with weight matrix, P = diag (p, p , . _; p ).

Substituting in equation (6.77) we get the solution, i.e. the weighted mean of the sample, as

n

;6.8o)

s pi. . . _ i i

X

n

£ p.

i

i=l

equals to one.

which agrees with the result in section 6Л.2. > when Zpj

i=l

Formula (6.8o) is the general formula used to compute the weighted mean of a sample of weighted observations.

results h_n , h^ and h.

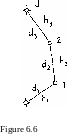Example 6.l6: Let us have a levelling line connecting two junction points, G and J, the elevations of which,H , H ,are known. The levelling line is divided into three sections d^, d^ and d^ long. Each level difference h^, h^ and h^ was observed^with

The observations h. are considered

uncorrelated with variances proportional to the corresponding lengths d., i = 1, 2, 3.

It is required to determine the adjusted values of the elevations of points 1 and 2, i.e. and respectively _ь using the parametric adjustment. Solution

From the given data we have:number of observations n=3 ; number of unknowns u = 2. Therefore, we have.one redund­ant observation. The independent relationships between the observation* and the unknowns are written as follows (each relation > corresponds to one observation .)t

^hl	^= ^Hi	- hg ,
^h2	^= ^H2	"^Hl •
^h3	^= ^HJ

The above relations can be rewritten in the general form

used in the previous development:

A x = L 3,2 2,1 ЗД

where X = (H^, Hg) and

^Hl = ^hl ^{+ H}G = ^Ll > -E_± + H₂ = h₂ = l₂ j

H		^(hl ^+ ^HG^)
1
	=	2
EL		.^(h3-^Hj^}.
L 2,

~^H2 ^{= h}3 " ^HJ ^{= L}3 ' Putting this in matrix form, we get 1 0 -1 1 0 -1

The corresponding set of observation equations are: H₁₌H_G+ (n_1+Vl) .

-н_х + н₂ = (h₂ + v₂) ,

H₂ = -Hj + (h₃ + v₃) .

These observation equations can be written in matrix form as:

v = a x - l ,

3,1 3,2 2,1 3,1

where:

(h_x '+ h_g)

V = 3,1

X = 2,1

L =

(h₃ - _Hj)

and the design matrix A is given by

1 0

3,2

We assumed that the observed values h^, h^ and h^ are uncorrelated. We will also assume that HL and H_T are errorless, Hence:

E- = diag (S-² , , ) .

2

But S- is proportional to d^, i = 1, 2, 3; i

thus

Zj- = к diag (d_l5 dg, d^). Further ₅ we choose к =1 and we get

P = к Zjf¹ = diag (i-, |-, |-) .

Applying the method of least-squares the normal equations are

Г

T

N = A PA =

where

a N X	=	U
2,2 2 51	2
i -i	0		^-1 ^dl
0 1 L	-1		0

о 0 ^d3

1 0

-1 1

0 -1

This gives

N 2,2

_{d2 ' 4}

and

T —

U = A PL

1-10 0 1-1

0 0

=T~ 0

T- 0

0 v~

(_{4 +}

(Eg -

Hence

A ^{+ H}G

U =

^d2

h.

_{h„ - H,}

N U

2,2 2,1

The solution X is given Ъу

r¹

2,1

where

-1 ^dl ^d2 ^d3 ^{N =} (d_n+ d + dj

1_ d.

^d2 ^dl ^d2 J

Performing the multiplication N^-1U and realizing that

X = (H . H ),we obtain: l' 2

d,

H.

_{1 " HG + El + Ed. (HJ " HG ~f V»}

11 ¹

^H2 ^{= H}J

Now, we compute the residuals v^ from the equation V ■ AX - L and find

Finally, we compute the adjusted observations from L = L + V ,

Remembering that EL and H_ are assumed errorless we get:

VJ J

^hi ⁼ \ ⁺ V i = 1_? 2, 3.

A local levelling network composed of 6 sections ^shown in Figure 6.7;vas observed. Note that the arrow heads indicate the direction of increasing elevation . The following table summarizes the observed differences in heights lu along with the corresponding length of each section.

Section	i , Stations		- h. i	length Ji.
No.	from	to	(m)	(km) ^1
1	a	с	6.16	k
2	a	d	12.57	2
3	с	d	6Л1	2
h	a	b	1.09	h
5	b	d	11.58	2
6	b	с	5.07	k

Assume that the variances S- , i = 1, 2, ... ^ 6, are

. i

proportional to the corresponding lengths £^. The elevation

H of station a is considered to be 0 metres. It is

a

required to adjust this levelling net by the parametric method of adjustment and deduce the least-squares estimates

A /4

, H_Q , and for the elevations H^, and of the points b, с , and d.

Solution:

From the given data we have - number of independent obser- . vations: n = 6, number of unknowns: u = 3. Hence we have 3 redundant observations_y i.e. 3 degrees of freedom . Our mathematical model in this case is linear, i.e.

A X = ■ L j

6,3 3,1 6,1

where

X = (H H , H _я) *

зд ■ ^ ^{c d}

The 6 independent observation equations will be ( one equation for each observed quantity):

⁵l^+Vl ^{= H}c-^Ha ^{= H}c-°-^{0 = H}c'

⁵2^+V2 ^{= H}d-^Ha ^{= H}d-°-^{0 = H}d'

^й3 ⁺ Y^=Hd-^Hc >

4 ⁺ \ = *b " ^Ha ^e =b " °'° = =b '

^E5 ^{+ y}5"^Ha-V

- ^£6^+V6^:"^Hc-V-

The above set of equations can be rewritten in the following

form, after substituting the values of 1ь :

v H - 6.l6 *

1 с

^v₂ ⁼ ^d ^12-57 >

v_o = -H + H, 6.Ul >

3 с d

v. = -у ₊ H_d - 11.58 ,

v₆= _g_{b +} S_c - 5.0T