Вопрос 17. Топологические пространства

Основные понятия теории метрических пространств- предельная точка, точка прикосновения, замыкание множества вводились с помощью понятия окрестности точки. Окрестность точки давала важный пример так называемого открытого множества.

Можно встать на другой путь и, не вводя понятия расстояния, аксиоматически определить в данном множестве М систему открытых множеств. Этот путь приводит к более широкому, чем метрические пространства, классу топологических пространств.

Определение. Пусть - некоторое множество. Топологией в называется любая система подмножеств , обладающая следующими свойствами:

1.

2. (объединение любого количества подмножеств из принадлежит ).

3. 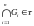(пересечение конечного числа подмножеств из лежит в ).

Определение. Множество и система подмножеств образуют топологическое пространство 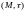, которое обозначим .

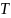Определение. Множество 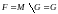(то есть дополнение открытого множества ) называется замкнутым.

Из законов двойственности имеем:

Это означает, что любое пересечение замкнутых множеств - замкнутое множество и объединение конечного числа замкнутых множеств - тоже замкнутое множество.

Определение. Совокупность 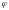открытых множеств называется базой топологического пространства , если любое открытое множество в есть объединение некоторых подмножеств из .

Таким образом, топология состоит из множеств, получаемых в результате объединений элементов базы.

Определение. Назовем окрестностью точки x в топологическом пространстве 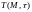любое открытое множество , для которого .

Введённые для метрических пространств определения предельной точки, свойства замкнутых множеств, понятие замыкания множества дословно переносятся на топологические пространства. На топологическое пространство также легко переносятся понятие сходящейся последовательности:

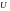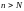последовательность , , сходится к для любой окрестности точки x существует такое, что для всех имеем .

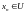Однако свойства общих топологических пространств могут значительно отличаться от изученных свойств метрических пространств. Если добавить некоторые дополнительные аксиомы, то свойства полученных топологических пространств будут более похожими на привычные свойства метрических пространств.

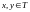
Например, добавим аксиому отделимости Хаусдорфа: для любых двух точек 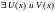- окрестности такие, что .

В заключение отметим, что метрические пространства представляют собой топологические пространства (в которых открытые множества – объединения окрестностей точек). Но не всякое топологическое пространство является метрическим. Топологическое пространство, топологию в котором можно задать с помощью расстояния, называется метризуемым.

Вопрос 20. Пространство . Компактные множества в

1. Пространство .

- арифметическое n-мерное пространство, состоящее из точек ;

это метрическое пространство с расстоянием ,

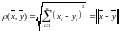где 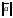- норма вектора , определяется как .
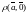