2. Примерная памятка для самоанализа урока учителем

1. Какова характеристика реальных учебных возможностей учащихся? Какие особенности учащихся при планировании данного урока?

2. Каково место данного урока в теме, разделе, курсе? Как он связан с предыдущими, на что в них опирается? Как этот урок работает на последующие уроки, темы, разделы? В чем специфика этого урока? Каков его тип?

3. Какие задачи решались на уроке:

- образовательные,

- воспитательные,

- задачи развития?

- Была ли обеспечена их комплексность? Взаимосвязь? Какие задачи были главными, стержневыми? Как учтены в задачах особенности класса, отдельных групп школьников?

4. Почему выбранная структура урока была рациональна для решения этих задач? Рационально ли выделено место в уроке для опроса, изучения нового материала, закрепления, домашнего задания и т. п.? Рационально ли было распределено время, отведенное на все этапы урока? Логичны ли «связки» между этапами урока?

5. На каком содержании (на каких понятиях, идеях, положениях, фактах) делался главный акцент на уроке и почему? Выбрано ли главное, существенное?

6. Какое сочетание методов обучения избрано для раскрытия нового материала? Дать обоснование выбора методов обучения.

7. Какое сочетание форм обучения избрано для раскрытия нового материала и почему? Необходим ли был дифференцированный подход к учащимся? Как он осуществлялся и почему именно так?

8. Как организован был контроль усвоения знаний, умений и навыков? В каких формах и какими методами осуществлялся? Почему?

9. Как использовался на уроках учебный кабинет, какие средства обучения? Почему?

10. За счет чего обеспечивалась высокая работоспособность учащихся в течение урока?

11. За счет чего на уроке поддерживалась хорошая психологическая атмосфера общения? Как было реализовано воспитательное влияние личности учителя?

12. Как и за счет чего обеспечивалось на уроке и в домашней работе учащихся рациональное использование времени, предупреждение перегрузки учащихся?

13. Запасные методические «ходы» на случай непредвиденной ситуации.

14. Удалось ли полностью реализовать все поставленные задачи? Если не удалось, то какие и почему? Когда учитель планирует восполнение нереализованного?

3. Заполнить таблицу размерности n*n:

1 1 1 … 1

0 2 2 … 2

……….

0 0 0 … n

program lab39;

type mas=array[1..10, 1..10] of integer;

var n,i,j:integer;

a:mas;

begin

writeln('Vvedite razmernost matrici (<10): ');

readln(n);

for i:=1 to n do

for j:=1 to n do

begin

if j<i then a[i,j]:=0

else a[i,j]:=i;

end;

for i:=1 to n do

begin

for j:=1 to n do

write(a[i,j],' ');

writeln;

end;

end.

Билет №12

1. Условный экстремум: функция Лагранжа, метод множителей Лагранжа.

Конечномерной экстремальной задачей с ограничениями типа равенств называется задача в E_n:

Пусть X E_n. Найти

F₀(x)extr; (1)

при ограничениях: F_i(x)=0, i=1,…,m, x=(x₁, x₂, …, x_n), m<n, x  X. (2)

Далее считаем, что все функции F_i (i=0, 1, … ,m) в X непрерывно дифференцируемы (в том смысле, что все частные производные F_i / x_i (k = 1, … , n) существуют и непрерывны в X).

В связи с этим вводится понятие условного экстремума.

Пусть Y множество точек x, для которых выполняется равенства (2). По определению точка x^*X есть точка локального условного минимума (максимума) функции F₀(x) при наличии ограничений (2), если x^*Y и существует  > 0 такое, что для всех x Y, удовлетворяет неравенству:

имеет место

F₀(x) F₀(x^*), (в случае минимума)

F₀(x) F₀(x^*), (в случае максимума).

Точка локального условного максимума или минимума называется точкой локального экстремума.

По определению точка x^*  X есть точка (глобального) условного минимума (максимума) функции F₀(x) при наличии ограничений (2), если x^*Y и имеет место для всех x  X

F₀(x) F₀(x^*), (в случае минимума)

F₀(x) F₀(x^*), (в случае максимума).

Множество всех точек минимума и максимума функции на множестве Y принято называть точками экстремума функции на этом множестве или, просто, точками экстремума.

Отметим одну теорему из математического анализа:

Теорема Вейерштрасса.

Если функция u = f(x), xM (M  Rⁿ), непрерывна на замкнутом ограниченном множестве M, то она достигает на этом множестве своих точных верхней и нижней граней (то есть решение задачи f(x)  max (min) существует).

Следствие. Если функция u = f(x) непрерывна на Rⁿ и lim f(x) = +  при x   (lim f(x) = -  при x  ), то f достигает своего абсолютного минимума (максимума) на любом замкнутом подмножестве R^*.

Это теорема и ее следствие часто используется при решении экстремальных задач и выступают самостоятельно и независимо от приведенных ниже методов.

Метод множителей Лагранжа является классическим методом решения экстремальных задач с ограничениями.

Классический подход к решению задачи (1), (2) дает метод множителей Лагранжа. Суть этого метода в следующем. Вводится функция Лагранжа

λ = (λ₀, λ_1, … _, λ_m) (3)

от переменных x₁, x₂, …, x_n, λ₀, λ_1, … _, λ_m, λ  E_m+1.

Оказывается, если x^* = (x₁^*, x₂^*, …, x_n^*) – точка локального минимума или максимума функции F₀(x) на множестве X, то необходимо существуют числа (λ₀, λ_1, … _, λ_m), не равные все одновременно нулю, называемые множителями Лагранжа, также, что

, i = , (4)

то есть векторы

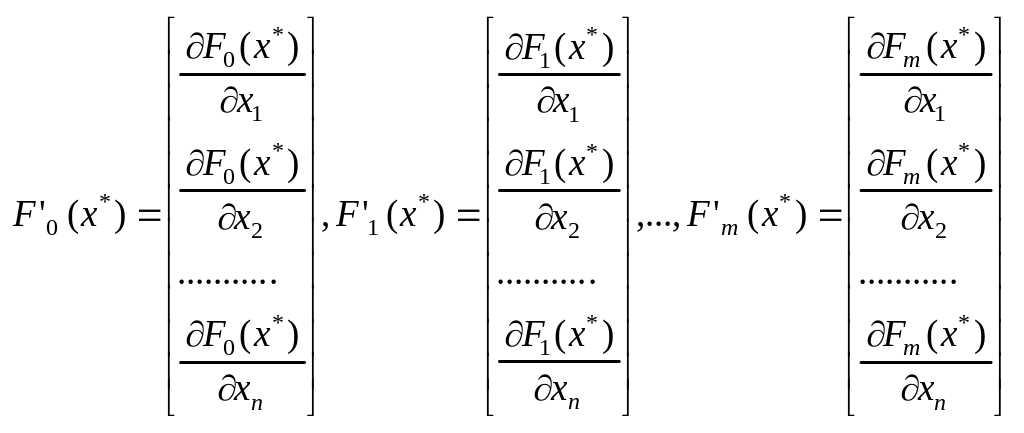
будут в точке x^* линейно зависимы.

Таким образом, для определения x^*, λ^* получается n+m уравнений:

с n+m+1 неизвестными. Следует учесть, что множителями Лагранжа определены при этом с точностью до пропорциональности. Если известно, что λ₀≠0, то можно, умножив все λ_i на константу, добиться равенства λ₀=1. Тогда число уравнений сравнятся с числом неизвестных. Однако заметим, что не исключен случай λ₀=0. Случай λ₀≠0 обосновывается следующим образом:

Для того чтобы λ₀≠0, достаточно, чтобы векторы F’₁(x^*), … , F’_m(x^*) были линейно независимы.

Действительно, векторы F’₀(x^*), F’₁(x^*), … , F’_m(x^*) образуют линейно зависимую систему. В нашем утверждении ее подсистема F’₁(x^*), … , F’_m(x^*) линейно независима, поэтому F’₀(x^*) можно линейно выразить через F’₁(x^*), … , F’_m(x^*), но тогда λ₀≠0.

Из этого следует правило решения задачи (1), (2).

Правило решения экстремальной задачи с ограничениями типа равенств.

1. Составить функцию Лагранжа

2. Выписать необходимое условие экстремума

(*)

3. Рассмотреть n уравнений (*) вместе с m уравнениями ограничениями

(**)

Полученная система содержит n+m уравнений с n+m+1 неизвестными x₁, x₂, …, x_n, λ₀, λ_1, … _, λ_m.

Несмотря на то, что система содержит число неизвестных на одно больше, чем число уравнений, данную систему можно свести к системе с n+m неизвестными, рассмотрев случаи λ₀=0 и λ₀≠0 (Чаще всего полагают λ₀=1 или λ₀=-1, когда λ₀≠0). Тогда в (*) – (**) число уравнений будет равно числу неизвестных.

4. Найти стационарные точки, то есть допустимые решения системы уравнений (*) – (**), в которой не все множители Лагранжа равны нулю.

Отыскать решение среди всех стационарных точек или доказать, что решения нет.