6 Декартові координати у просторі. Кути між прямими і площинами.

М етод координат - це спосіб визначення положення точки, фігури або тіла за допомогою чи­сел. або інших символів. Числа, за допомогою яких визначається положення точки, називають її координатами.

. Нехай х, у, z — три попарно перпендикулярні координатні прямі, які перети­наються в точці О (рис. 248 або рис. 68 із підручника). Ці координатні прямі називаються координатними осями: вісь х, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно, точку О називають почат­ком координат.

Кожна вісь точкою О розбивається на дві півосі — додатну, позначе­ну стрілкою, і від'ємну.Площини, які проходять через х і у, х і z, у і z, називають координат­ними площинами і позначають відповідно: ху, хz, уz. Координатні пло­щини розбивають весь простір на вісім частин, які називають октан­тами. Візьмемо довільну точку А і проведемо через неї площину, паралельну уz (рис. 249). Вона перетинає вісь х у деякій точці А₁. Координатою х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка ОА₁; додатне, якщо точка А₁ лежить на додатній півосі х, від'ємне, якщо вона лежить на від'ємній півосі і дорівнює нулю, якщо точка А, збі­гається з точкою О. Аналогічно означаємо координати у і г точки А. Координати точки записуватиме­мо в дужках поряд із позначенням точки: А(х; у; z), інколи познача­тимемо точку просто її координата­ми (х; у; z).

Якщо задано систему координат у просторі, то кожній точці просто­ру можна поставити у відповідність три впорядковані дійсні числа х, у, z, і навпаки: кожній трійці чисел х, у, z — єдину точку простору

.

Вивчаються в 10 кл. Крім взаємно перпендикулярних осей х та у вводиться вісь z. Точка має вже три координати (х;у;z).

Кутом між прямою та площиною називається кут між цією прямою і її проекцію (ортогональною) на площину.

Якщо пряма перпендикулярна до площини, то кут між нею й площиною вважається таким, що дорівнює , а між паралельними прямою та площиною таким, що дорівнює .

Кут між прямою та площиною і кут між цією прямою й перпендикуляром до площини в сумі дорівнюють

На рисунку

Кут між паралельними площинами вважається таким, що дорівнює .

Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної площини.

Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок).

Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz.

Прямі Ox, Oy, Oz називаються координатними осями (Ox — вісь абсцис, Oy — вісь ординат, Oz — вісь аплікат).

Точка їх перетину О — початок координат, площини Oxy, Oxz, Oyz — координатні площини.

Точка О розбиває кожну з осей координат на дві півпрямі — півосі. Домовимось одну півось називати додатною, а другу — від’ємною.

Візьмемо тепер довільну точку А й проведемo через неї площину, паралельну площині Oyz. Вона перетинає вісь Ox у деякій точці . Координатою х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка .Це число додатне, якщо точка лежить на додатній півосі Оx, і від’ємне, якщо точка лежить на від’ємній півосі. Якщо точка збігається з точкою О, то вважаємо, що Аналогічно означаємо координати y і z точки A. Координати точки записуватимемо в дужках поряд із буквеним позначенням точки: .Якщо точка A не належить жодній із координатних площин, то ці площини разом із трьома паралельними їм площинами, які проходять через точку А, обмежують прямокутний паралелепіпед.

7. Об’єми многогранників. Загальні властивості об’ємів многогранників.

Кожне геометричне тіло займає частину простору.

Об'ємом геометричного тіла будемо називати додатне число, яке характеризує частину простору, що займає геометричне тіло, і за­довольняє таким умовам:

1. Рівні тіла мають рівні об'єми.

2. Якщо тіло розбите на кілька частин, то його об'єм дорівнює сумі об'ємів усіх цих частин.

3. Об'єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці.

Куб, довжина ребра якого дорівнює одиниці довжини, називають одиничним.Об'єм одиничного куба приймають за одиницю об'єму, називаючи таку одиницю кубічною.Наприклад: кубічний сантиметр — це об'єм куба, ребро якого дорів­нює 1.

Виміряти об'єм, геометричного тіла — значить знайти число, яке показує, скільки одиничних кубів міститься в даному тілі.

Тіла, які мають рівні об'єми, називаються рівновеликими. На рис. 143 тіла а—д рівновеликі.

М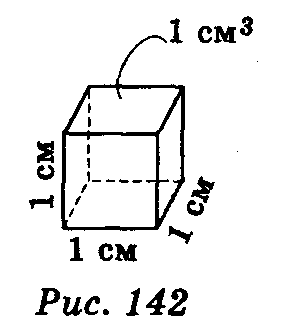 и будемо далі розглядати лише прості тіла — тіла, які можна розбити на скінчене число трикутних пірамід. Вивчені многогранники: призми, піраміди, зрізані піраміди — є простими тілами.

Перше уявлення про об'єми тіл і їх обчислення учні дістають у курсі математики 5 класу у зв'язку з вивченням прямокутного паралелепіпеда. В 11 класі вони повертаються до вивчення об'ємів на дедуктивній основі. В умовах роботи за підручником О. В. Погорєлова за аналогією з введенням поняття площі фігури в курсі планіметрії запроваджується поняття об'єму спочатку простих тіл. Так само формулюється означення об'єму простого тіла як додатної величини, числове значення якої має три властивості. Далі доводиться формула об'єму прямокутного пара­лелепіпеда. В останньому виданні підручника подано інший, коротший спосіб доведення цієї формули, ніж у попередніх, але теж з використанням ідеї граничного переходу.

Практика свідчить про те, що доведення формул об'єму похилого паралелепіпеда методом перетворення його додаткови­ми побудовами в прямокутний, як і доведення формули об'єму призми, не викликають в учнів особливих труднощів, якщо до того ж використати заздалегідь виготовлені моделі, що ілюстру­ють етапи перетворення. Важче сприймається учнями доведення формули об'єму трикутної піраміди.

Об’єм прямокутного паралелепіпеда дорівнює добутку площі основи на висоту паралелепіпеда.

Об’єм похилого паралелепіпеда дорівнює добутку площі основи на висоту.

Об’єм будь-якої призми дорівнює добутку площі її основи на висоту.

Об’єм похилої призми дорівнює добутку площі перпендикулярного перерізу на довжину бічного ребра.

Об’єм будь-якої піраміди дорівнює одній третій добутку площі її основи на висоту.

Об’єм будь-якої зрізаної піраміди дорівнює одній третій добутку висоти піраміди на суму площ двох її основ і кореня квадратного з добутку площ основ піраміди

У класах з поглибленим вивченням математики можливий ін­ший методичний варіант використання визначеного інтеграла для обчислення об'ємів тіл, що вивчаються в шкільному курсі. Спочатку вводяться поняття довільного циліндра і ко­нуса. Призма і піраміда в такому разі є окремими випадками ци­ліндра і конуса. Попередньо вводиться теорема про об'єм прямо­го циліндра. Спочатку вона обґрунтовується наочними міркуван­нями, а відтак доводиться строго.

Далі формулюється теорема про вираження об'єму простої фі­гури Т інтегралом, тобто

, де S(x)

Після цього доводять теореми про об'єм циліндра (зокрема, призми), об'єм конуса (зокрема, піраміди), кулі, тіл обертання.