Контрольные вопросы

1. В чем состоит геометрический способ вычисления вероятности событий?

§ 4. Аксиоматическое определение вероятности событий

4.1. Аксиоматическое построение теории вероятностей

Аксиоматическое построение теории вероятностей было предложено А. Н. Колмогоровым [3]. Исходным понятием этой теории является множество различных элементов, называемых элементарными собы­тиями. Это множество может быть конечным или бесконечным, несчетным или счетным. В последнем случае его можно записать в виде последова­тель­ности

,

где ( ) – элементарное событие.

На основе него строится множество подмножеств множества . Элементы множества называют случайными событиями. Над ними определяют действия сложения, умножения и взятия противоположного события. Суммой двух множеств является множество элементов, каждый из которых является элементом хотя бы одного из складываемых множеств. Произведением двух множеств (событий) называется множество элементов, каждый из которых входит в состав каждого из перемножаемых множеств. Противо­положным множеству называется множество , состоящее из всех элементов множества , не являющихся элементами множества . В состав множества включают также пустое множество , не содержащее ни одного элемента.

На множестве определяется функция вероятности , удовлетворяю­щая следующим аксиомам.

Аксиома 1. Каждому случайному событию ставится в соответствие неотрицательное число

, (1)

называемое его вероятностью.

Аксиома 2. . (2)

Аксиома 3. Если события попарно несовместны, т.е. (где и ), то

. (3)

4.2. Свойства функции вероятности

Из этих аксиом получаются следующие следствия:

(см. формулу (1.2.4)); (1)

(см. (1.2.5)); (2)

то (см. формулу (1.2.6)); (3)

(см. формулу (1.2.7)); (4)

(5)

Формула (5) называется теоремой сложения вероятностей произвольных событий.

. (6)

Настоящее свойство следует из свойств, выраженных соотношениями (5) и (3).

1. Обобщая свойство (6) на произвольное число событий, получаем

. (7)

Отметим сначала, что свойства 1-3 классической функции вероятности, представленные формулами (1.2.1)–(1.2.3), составляют содержание аксиом и выполняются автоматически. Приступим к доказательству остальных свойств функции вероятности.

1. .

Доказательство

Очевидно

.

Т.к.

,

то

.

Следовательно,

. 

2. .

Доказательство

Очевидно

.

Т.к.

,

то

. 

3. Если , то .

Доказательство

Пользуясь свойствами операций над событиями, приведенными в табл. 2.6.1, получаем следующую цепочку соотношений

.

Поскольку , то выполняется соотношение . Это обстоятельство позволяет завершить цепочку тождественных преобразований в виде

Т.к.

,

то, вычислив функцию вероятности от обеих частей последнего ра­венства, получим

. 

4. .

Доказательство

Т. к. согласно аксиоме 1 , то из формулы (2) следует, что . Снова, учитывая аксиому 1, получаем . Окончательно

. 

5. - теорема сложения вероятностей произвольных событий.

Доказательство

Пусть события и не являются несовместными. Для доказательства настоящей теоремы воспользуемся аксиомой 3. Для этого событие представим в виде суммы несовместных событий. Возможны три следующих представления:

1. ;

2. ;

3. .

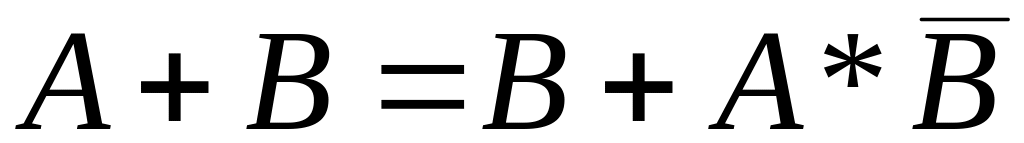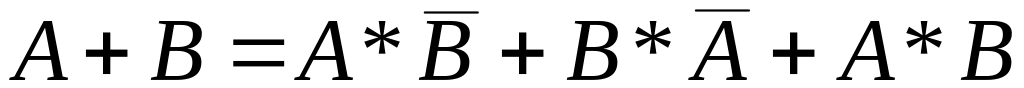В справедливости этих соотношений можно убедиться или с помощью диаграмм Венна или аналитически. Действительно, например, для первого из соотношений получаем

.

Поскольку сложение событий обладает свойством коммутативности, то справедливость второго равенства следует из справедливости первого. Для обоснования третьего разложения суммы выполним следующие преобразования

.

Применяя аксиому 3 к трем разложениям суммы на частные случаи, получим

1. ;

2. ;

3. .

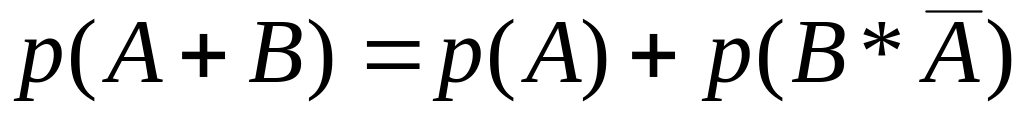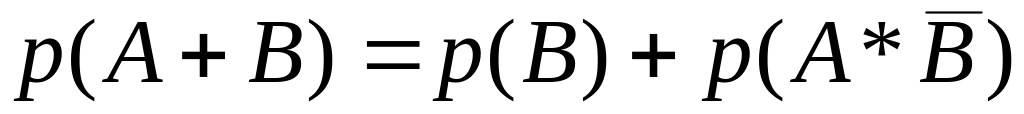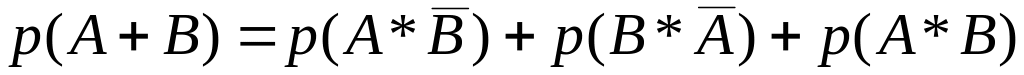Выражая из первых двух уравнений вероятности и и подставляя их в третье, получим

.

Из последнего равенства после тождественных преобразований получаем следствие 5.