Операционное исчисление Содержание:

1. Функция оригинал и изображение по Лапласу

2. Теоремы преобразования Лапласа

3. Методы определения оригинала по известному изображению

4. Решение дифференциальных уравнений и систем операционным методом

5. Примеры решения задач

6. Вопросы и задачи для самостоятельной работы

1. Функция оригинал и изображение по Лапласу

Функцией- оригиналом - называют функцию действительного аргумента

удовлетворяющую условиям:

1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.

2) функция при возрастает не быстрее показательной функции, т.е. существ.уют такие постоянные что

3) на любом конечном отрезке положительной полуоси функция и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.

Простейшей функцией - оригиналом является единичная функция Хевисайда

(1)

Если функция не удовлетворяет условию то произведение уже ему удовлетворяет, т.е. будет оригиналом.

Для простоты записи множитель опускается, например, пишут вместо вместо и т.д.

Изображением функции по Лапласу (преобразованием по Лапласу) называют функцию комплексной переменной определяемую соотношением

(2)

Интеграл (1.2) называют интегралом Лапласа.

Функция определяется в полуплоскости и является в этой области аналитической функцией.

То, что функция комплексной переменной является изображением по Лапласу функции действительного аргумента обозначается или

Изображение элементарных функций получается непосредственно с помощью интеграла (2).

Пример 1 Найти изображение по Лапласу функции

РЕШЕНИЕ

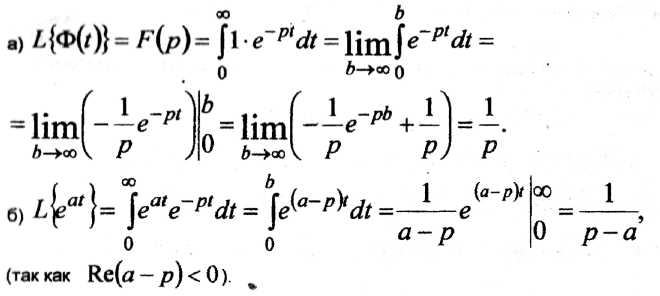
Таким образом, получаем

Преобразование, основанное на интеграле Лапласа (2), обладает линейными свойсгыами.

1. Преобразование суммы функций равно сумме преобразований этих функций

2 Постоянный множитель можно выносить за знак преобразования:

Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:

(3)

Пример 2. Найти изображение функции

РЕШЕНИЕ

Используем формулу (2) для функции Тогда

2. Теоремы преобразования Лапласа

1. Теорема подобия Если то для любого постоянного а > 0

(4)

Пример 3. Найдем Из примера 2 _.По Формуле (4)

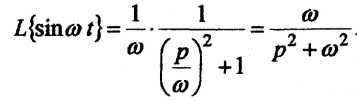
2. Дифференцирование оригинала Если то

(5)

Методом индукции на основании формулы (5) получены формулы изображения высших производных:

(6)

(7)

(8)

Пример 4. Определим Так как

то по формуле (5) получим:

3. Дифференцирование изображения. Если то т.е. дифференцирование изображения сводится к умножению на оригинала. В общем случае,

(9)

Пример 5. Определить изображения функций

РЕШЕНИЕ

Так как

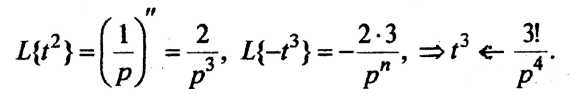
В общем случае

4. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р:

(10)

Пример 6. Найти изображение функци

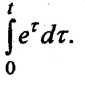
РЕШЕНИЕ Так как то по формуле (10)

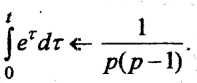
5. Интегрирование изображения. Интефирование изображения равносильно делению на t оригинала (если существует конечный предел

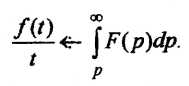(11)

Пример 7. Найдем изображение функции

Так как то по формуле (11) получаем

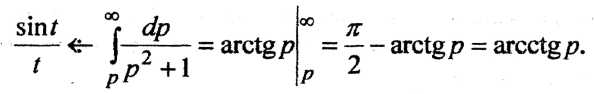
6. Теорема смещения При умножении оригинала на изображение получается смещение аргумента на

(12)

Пример 8. В примерах 3, 4, 5 найдены изображения функций По формуле (12) находим:

7. Теорема запаздывания. "Включение" оригинала с запаздыванием на равносильно умножению изображения на

(13)

В данной формуле важно подчеркнуть, что функция поэтому она умножена на единичную функцию Хевисайда с запаздыванием . График единичной функции Хевисайда с запаздывающим аргументом показан на рисунке 1.

Изображение

к примеру 9

Функция Хевисайда с запаздыванием применяется для записи кусочно-аналитического оригинала и определения его изображения.

Пример 9. Функция - оригинал задана в виде

Выписать функцию одним выражением и найти ее изображение.

РЕШЕНИЕ

График функции изображен на рисунке 2.

Чтобы можно было применить формулу (13), второе слагаемое в последнем выражении преобразуем:

Тогда

Применим к последнему выражению формулу (13):

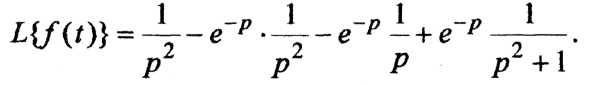
На основе рассмотренных теорем и примеров к ним можно составить таблицу преобразования Лапласа. В таблице приведены наиболее часто встречающиеся преобразования. Здесь - различные постоянные.

Таблица 1 — Преобразования Лапласа

Продолжение таблицы 1