
- •11. Анализ парных наблюдений в политологии: постановка задачи, применение критерия знаков. (Бочарова а)
- •12. «Задача о двух выборках»: постановка задачи. Критерий Стьюдента: алгоритм решения, ограничения метода. Пример использования в политологии.(Бочарова а)
- •X (демократии): 3, 6, 2, 11, 7, 5, 15.
- •13. Коэффициент корреляции Пирсона: содержательный смысл, формула расчета. Проблема устойчивости. Примеры применения в политологии (прошлый год)
- •Общие положения
- •Алгоритм действий
- •Vs h1: модель лучше константы.
- •Vs h1: β1 мнк с крышкой ≠ 0.
10. Понятие выборочной оценки. Точечная и интервальная оценка. Понятие «доверительный интервал». Методы расчета доверительного интервала для среднего нормальной совокупности. Применение в политологии. (Баданова Р)
Выборочные оценки. Оценкой неизвестного параметра Z называют любую функцию n переменных от выборки:
Z n = f (x1, x2, …x n)
Поскольку оценка является функцией от случайного вектора (выборки), она сама является случайной величиной, распределение которой зависит от числа наблюдений n и оцениваемого параметра Z.
Существуют следующие виды оценок:
Оценка неизвестных параметров распределения:
точечные оценки параметров распределения, например оценка математического ожидания, дисперсии, моментов распределения,
интервальные оценки – доверительные интервалы – интервалы, в которых находятся параметры распределения с доверительной вероятностью.
Пусть
неизвестен параметр распределения .
Любая функция
.
Любая функция
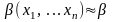 на выборке
на выборке
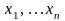 называется точечной оценкой
.
Оценки тоже являются случайными
величинами.
называется точечной оценкой
.
Оценки тоже являются случайными
величинами.
Требования к оценкам:
Несмещенность
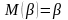
Состоятельность

Эффективность (по сравнению с другими оценками) – если дисперсия оценки меньше дисперсий других оценок.
Можно
показать, что несмещенная оценка
состоятельна, если ее выборочная
дисперсия стремится к нулю при
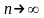 .
.
Интервальные оценки – доверительные интервалы – интервалы, в которых находятся параметры распределения с доверительной вероятностью, также являются оценками неизвестных параметров распределения, как и выборочные оценки или гистограмма
Доверительный интервал – это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром; содержит этот параметр с заданной вероятностью. Иными словами, это диапазон колебаний истинных значений; он показывает диапазон вокруг значения статистики, в котором находится истинное значение этой статистики с определенным уровнем доверия (надежности).
Величины, полученные в исследованиях на выборке, отличаются от истинных величин в целом вследствие влияния случайности. Так, 95% доверительного интервала означает, что истинное значение величины с вероятностью в 95% лежит в пределах рассчитанного интервала. Доверительные интервалы помогают сориентироваться, соответствует ли данный диапазон значений представлениям о ситуации в целом. Величина ДИ характеризует степень доказательности данных, в то время как значение р указывает на вероятность отклонения нулевой гипотезы.
Доверительный
интервал – интервал
![]() где
где
![]() такой, что
такой, что
![]()
Х1, …, Хn – независимая выборка,
![]() - неизвестный
параметр,
- неизвестный
параметр,
![]() - доверительная
вероятность, значение которой выбирается
заранее (это определяется конкретными
практическими приложениями; часто берут
значения 0.9, 0.95, 0.99).
- доверительная
вероятность, значение которой выбирается
заранее (это определяется конкретными
практическими приложениями; часто берут
значения 0.9, 0.95, 0.99).
Доверительные интервалы для среднего задают область вокруг среднего, в которой с заданным уровнем доверия содержится «истинное» среднее выборки. Можно построить доверительный интервал. для любого р-уровня: например, если среднее равно 23, а нижняя и верхняя границы для р=0,5 равны 19 и 27 соответственно, то можно заключить, что с 95% вероятностью среднее выборки больше 19 и меньше 27.
![]() - доверительный
интервал по Стьюденту, где
- доверительный
интервал по Стьюденту, где
- среднее значение генеральной совокупности,
![]() - ошибка среднего
арифметического, вычисляемая по формуле
- ошибка среднего
арифметического, вычисляемая по формуле
![]() ,
,
 ,
,
T
– число Стьюдента (табличное значение,
которое находится исходя из уровня
доверительной вероятности
![]() и числа степеней свободы k
= n).
и числа степеней свободы k
= n).
Пример:
Желая узнать, сколько часов в неделю
дети проводят у телевизора, социологическая
служба обследовала 100 учеников некого
города, в результате чего оказалось,
что в среднем это число равно
![]() 27,5.
Из прошлой практики известно, что
стандартное отклонение (
27,5.
Из прошлой практики известно, что
стандартное отклонение (![]() X)
генеральной
совокупности равно 6 (часов). Найдем
доверительный интервал с доверительной
вероятностью 0,95 для числа часов в неделю,
проводимых ребенком у телевизора.
X)
генеральной
совокупности равно 6 (часов). Найдем
доверительный интервал с доверительной
вероятностью 0,95 для числа часов в неделю,
проводимых ребенком у телевизора.
Поскольку доверительная вероятность b = 0,95, из таблицы находим T = 0,96, и границы интервала доверия будут такими:
ẋ
± T*![]() ,
,
Доверительный интервал имеет вид (26.32; 28.68)
11. Анализ парных наблюдений в политологии: постановка задачи, применение критерия знаков. (Бочарова а)
У математической статистики есть две крупные задачи – оценивание (делаем вывод по выборке о генеральной совокупности) и проверка статистических гипотез (гипотез о характере распределения случайных величин).
Критерий знаков (sign test) — статистический критерий, позволяющий проверить нулевую гипотезу, что выборка подчиняется биномиальному распределению с параметром p=1/2. Критерий знаков можно использовать как непараметрический статистический критерий для проверки гипотезы об отсутствии сдвига (отсутствия эффекта обработки) в двух связных выборках (исследованиях одной и той же выборки до и после какого-то события).
Также называется «задача об одной выборке».
Дж. Арбетнот. 1712 г. Ненаблюдаемая гетерогенность
Можно ли списать разницу в наблюдениях на фактор случайности или нет?
H0: нет никаких различий между двумя связными выборками. P(Z> 0)=P(Z<0)=1/2.
H1 (альтернативная, конкурирующая гипотеза): выборки различаются P(Z> 0)≠P(Z<0).
Допущение: если происходим маловероятное событие при Р0, мы рассматриваем его как невозможное при H0. Определяем уровень значимости. Пусть альфа = 0,05.
Допустим, исследуются электоральные предпочтения на фокус-группе до и после просмотри агитационных материалов и их обсуждения.
i |
Мнение до |
Мнение после |
1 2 3 4 5 6 7 8 9 … n |
+ - 0 _ _ _ + - - … |
+ + - - + - 0 + - -
|
>15
< 10
n = 25 (все, у кого отношение изменилось: и в худшую, в лучшую стороны).
Допустим, изучаем тех. У кого отношение улучшилось (примем их за S).
S – B (25; 0,5),
аппроксимация нормальности,
ES = np = 25*0,5 = 12,5
Переходим с стандартному нормальному распределению.
Ψ = (S – ES) / (DS)0,5 = (S – 0,5n) / 0,5 (n)0,5 = (2S – n) / (n)0,5
Определяем доверительную зону (зону высоковероятных значений). При выбранном уровне значимость [ -1,96; 1,96].
Рассчитываем наблюденное значение статистики.
В нашем случае S = 15.
Ψ = (2*15 – 25) / 5 = 1.
Критерий: отвергать Ho в пользу H1 на уровне значимости альфа, если наблюденное значение статистики критерия не попало в доверительную зону (или по модулю превысило значение процентной точки).
В рассматриваемом случае нет оснований отвергнуть нулевую гипотезу (следовательно, различий нет, ролик нейтрален).
12. «Задача о двух выборках»: постановка задачи. Критерий Стьюдента: алгоритм решения, ограничения метода. Пример использования в политологии.(Бочарова а)
Проблема, связанная с задачей сравнения двух выборочных совокупностей, часто встречающаяся.
Например, в политологии существует давно известное «условие М.С. Липсета», заключающееся в том, что уровень демократического развития тем выше в стране, чем успешнее ее экономическое развитие. Однако, к примерку, совсем по-иному трактует эти два процесса не менее авторитетные исследователь С. Хантингтон, предположивший в книге «Политический порядок в меняющихся обществах», что для экономической модернизации необходима стабильность и порядок, допускающий ограничение демократических свобод. Известно, что многие исследователи (Р. Барро, А. Пшеворский, А., Лимонджи и др.) проводили исследования, направленные на выявление различий в экономическом развитии демократий и автократий.
Для изучения этого вопроса необходимо иметь две выборки (демократии и автократии) и воспользоваться одним из статистических методов, например, критерием Стьюдента (и сравнить их средние значения).
t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Критерий Стьюдента является параметрическим методом (основан на дополнительном предположении о нормальности выборки данных).
Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
H0: F=G.
H1: F≠G (гипотеза сдвига).
Т.е. отвечаем на вопрос, можно ли сказать, что ax < ay (т.е. среднее первой выборки меньше среднего второй выборки)? А просто средние не берем, так как это робастная статистика, а просто медиану не берем, т.к. это все случайные числа (а критерий уходит от фактора случайности). ВЕРНО?
Рассмотрим на примере задачи.
Допустим, выборки: ВВП на д.н. (тыс. долл.)
