
- •Екзаменаційний білет № 21
- •Поверхневi iнтеграли. Формули Грiна, Стокса, Остроградського.
- •Постановка задачі багатокритеріальної оптимізації. Метод послідовних поступок.
- •Екзаменаційний білет № 22
- •Криволiнiйнi iнтеграли. Умови незалежностi криволiнiйного iнтегралу вiд шляху iнтегрування..
- •22.2 Прийняття рішень в умовах ризику та невизначеності. Критерій Севіджа.
- •Екзаменаційний білет № 23
- •Основнi рiвняння прямої та площини у просторi.
- •Прийняття рішень в умовах конфлікту. Обережні стратегії.
- •Екзаменаційний білет № 24
- •24.1 Критерiй сумiсностi системи лiнiйних рiвнянь.
- •24.2Прийняття рішень в умовах конфлікту. Рівновага за Нешем.
- •Екзаменаційний білет № 25
- •25.1Лiнiйна залежнiсть та ранг системи векторiв, методи обчислення рангів.
- •Ранг матриці:
- •Методи обчислення рангів
- •25.2 Класифікація задач і процедур системного аналізу.
- •Екзаменаційний білет № 26
- •Лiнiйнi оператори скiнченно-вимiрних просторiв та їх матрицi.
- •Поняття складності системної задачі, спектри складності, трансобчислювальна складність.
- •Екзаменаційний білет № 27
- •27.1Власнi вектори та власнi числа лiнiйних операторiв.
- •27.2 Розкриття невизначеностей у задачах системного аналізу.
- •Розкриття ситуаційної невизначеності
- •3. Розкриття невизначеності в задачах взаємодії
- •Екзаменаційний білет № 28
- •28.1Лiнiйнi оператори простої структури.
- •28.2 Інформаційний аналіз системних задач.
- •Екзаменаційний білет № 29
- •29.1Лiнiйнi оператори дiйсних евклiдових просторiв.
- •29.2Сценарний аналіз як методологічна основа передбачення.
- •Екзаменаційний білет № 30
- •30.1Зведення квадратичних форм до канонiчного вигляду.
- •Метод Лагранжа.
- •30.2Метод аналізу ієрархій.
Екзаменаційний білет № 21
Поверхневi iнтеграли. Формули Грiна, Стокса, Остроградського.
Нехай
Ф – гладка обмежена двостороння поверхня
(якщо нормаль поверхні не змінює напрямку,
то поверхня наз-ся двосторонньою). Нехай
на цій поверхні задана ф-ція f(M), і крім
того в кожній точці М задана функція і
нормаль. Поверхню Ф розіб’ємо на n частин
і в кожній частині виберемо точку Мі
і складемо суму:
 ,
де
,
де
 –
елемент площіі поверхні (величина площі
і-тої ячейки розбиття Ф). Перейдемо до
границі при n,
тоді, якщо
–
елемент площіі поверхні (величина площі
і-тої ячейки розбиття Ф). Перейдемо до
границі при n,
тоді, якщо
 ,
то
,
то
 називається
поверхневим інтегралом 1-го роду.
Поняття поверхневого інтегралу 1-го
роду поширюється і на замкнуті поверхні.
називається
поверхневим інтегралом 1-го роду.
Поняття поверхневого інтегралу 1-го
роду поширюється і на замкнуті поверхні.
Нехай
Ф – гладка двостороння поверхня.
Зафіксуємо одну із сторін цієї поверхні
і розглянемо вектор-функцію
 ,
задану на Ф. Позначимо через
,
задану на Ф. Позначимо через
 проекцію
вектора F на напрямок нормалі
проекцію
вектора F на напрямок нормалі
 в точці
в точці
 .
Інтеграл
.
Інтеграл
 називається
поверхневим інтегралом
2-го роду від вектор-функції
F за вибраною стороною поверхні і
записують його так:
називається
поверхневим інтегралом
2-го роду від вектор-функції
F за вибраною стороною поверхні і
записують його так:
 .
Отже, за визначенням
.
Отже, за визначенням
 =
= .
При переході до іншої сторони поверхні
цей інтеграл змінює свій знак на
протилежний.
.
При переході до іншої сторони поверхні
цей інтеграл змінює свій знак на
протилежний.
Формула Гріна.
Якщо
функції P(x,y), Q(x,y) – неперервні в замкнутій
області D і мають неперервні частинні
похідні в цій області і існують невласні
інтеграли від кожної з функцій, то має
місце формула Гріна:
 .
.
Частинні
випадки формули Гріна:
Q(x,y)=х, P(x,y)=-y. Тоді
 .
.
Формула Стокса.
Теорема.
Нехай в деякому околі двосторонньої
поверхні S функції
 )
– неперервні разом з своїми частинними
похідними першого порядку,
)
– неперервні разом з своїми частинними
похідними першого порядку,
 замкнений
контур, який є межею поверхні S. Тоді має
місце формула Стокса:
замкнений
контур, який є межею поверхні S. Тоді має
місце формула Стокса:

 .Орієнтація
поверхні повина відповідати орієнтації
кривої:
.Орієнтація
поверхні повина відповідати орієнтації
кривої:
 .
.
x=x,
y=y, z=z(x,y),
 -
область, куди проектується.
-
область, куди проектується.

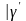 -
межа області
-
межа області

вектор
нормалі зад поверхні z=z(x,y):

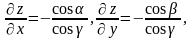 =
=
= .
.
 - аналогічно першому, потім знаходимо
середнє арифметичне і отримаємо нашу
формулу.
- аналогічно першому, потім знаходимо
середнє арифметичне і отримаємо нашу
формулу.
Ця формула узагальнює формулу Гріна на просторовий випадок.
Формула Остроградського.
Теорема.
Функції
 )
– неперервні в замкнутій області V
разом зі своїми похідними
)
– неперервні в замкнутій області V
разом зі своїми похідними
 ,
тоді :
,
тоді : ,
S–поверхня, яка обмежує об’єм V, n- вектор
нормалі до зовнішньої сторони,
,
S–поверхня, яка обмежує об’єм V, n- вектор
нормалі до зовнішньої сторони,
 -
вектор ф-я.
-
вектор ф-я.
 .
.
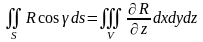 -
доведемо. Розіб’ємо елем тіло на скінч
кількість елем тіл для інтегр по x, y. Всі
межі мають Лебегову міру 0, отже на
інтеграл не впливають, всі інт по внутр
поверхні =0. Достатньо довести формулу
для тіла елем для інтегрув по x,y.
-
доведемо. Розіб’ємо елем тіло на скінч
кількість елем тіл для інтегр по x, y. Всі
межі мають Лебегову міру 0, отже на
інтеграл не впливають, всі інт по внутр
поверхні =0. Достатньо довести формулу
для тіла елем для інтегрув по x,y.
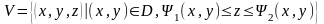 ,
,
 ,
,
 =|
=| =0,s1-верхня
основа,s2-нижня основа,s3-бічна поверхня.|=
=0,s1-верхня
основа,s2-нижня основа,s3-бічна поверхня.|= .
.
Постановка задачі багатокритеріальної оптимізації. Метод послідовних поступок.
Постановка задачі багатокритеріальної оптимізації. Будемо розглядати скінченно вимірні задачі багатокритеріальної максимізації:

де
Х – множина альтернатив, яка є множиною
з простору
 ;
; –
вектор критеріїв, який задається
відображенням
–
вектор критеріїв, який задається
відображенням
 –
множина індексів критеріїв, m – кількість
критеріїв. У таких задачах множина
альтернатив Х, як правило, виділяється
з якоїсь ширшої множини
–
множина індексів критеріїв, m – кількість
критеріїв. У таких задачах множина
альтернатив Х, як правило, виділяється
з якоїсь ширшої множини
 за
допомогою обмежень, що найчастіше
представляються у вигляді нерівностей:
за
допомогою обмежень, що найчастіше
представляються у вигляді нерівностей:

де –
числові функції, які визначені на D. При
цьому вважається, що і вектор критеріїв
–
числові функції, які визначені на D. При
цьому вважається, що і вектор критеріїв
 також визначений на D.
також визначений на D.
У
ролі множини D, як правило, виступає або
весь простір
 , або деяка його специфічна підмножина,
наприклад, невід'ємний ортант
, або деяка його специфічна підмножина,
наприклад, невід'ємний ортант
 ,
утворений усіма векторами з невід'ємними
компонентами:
,
утворений усіма векторами з невід'ємними
компонентами:
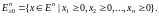
Практично,
множина D виділяється з
 за допомогою найпростіших і очевидних
обмежень на змінні.
за допомогою найпростіших і очевидних
обмежень на змінні.
Особливістю методу є те, що критерії багатокритеріальної задачі повинні бути попередньо впорядковані за зменшенням їхньої важливості, після чого вибір розв'язку задачі здійснюється шляхом виконання багатокрокової діалогової процедури. Діалогова процедура послідовних поступок складається з одного попереднього і m основних кроків (нагадаємо, що m – це кількість критеріїв).
0
– крок. Критерії впорядковуються за
зменшенням їхньої важливості (будемо
вважати, що
 )
за думкою ОПР.
)
за думкою ОПР.
і
– й крок ( ). Розв'язується однокритеріальна задача:
). Розв'язується однокритеріальна задача:

Позначимо
через
 її оптимальний розв'язок. Далі обчислюється
оцінка
її оптимальний розв'язок. Далі обчислюється
оцінка
 .
ОПР аналізує отриману оцінку й у випадку,
коли вона його не задовольняє, визначає
величину поступки
.
ОПР аналізує отриману оцінку й у випадку,
коли вона його не задовольняє, визначає
величину поступки
 за i-м критерієм, на яку він може погодитися
з метою покращення показників за іншими,
менш важливими критеріями. Якщо крок
не є останнім ( i <m ), то визначається
"уточнена" множина альтернатив
за i-м критерієм, на яку він може погодитися
з метою покращення показників за іншими,
менш важливими критеріями. Якщо крок
не є останнім ( i <m ), то визначається
"уточнена" множина альтернатив
 і
здійснюється перехід на наступний крок.
У протилежному випадку – альтернатива
і
здійснюється перехід на наступний крок.
У протилежному випадку – альтернатива
 вибирається як розв'язок багатокритеріальної
задачі і процедура закінчується.
вибирається як розв'язок багатокритеріальної
задачі і процедура закінчується.
На m-му кроці ОПР повинна чи погодитися з отриманою альтернативою, чи повторно виконати процедуру. У цьому випадку ОПР збагачується знанням про взаємозв'язок поступок за критеріями та значеннями менш важливих критеріїв.
Варто зауважити, що метод не обмежує можливості ОПР у виборі ефективних альтернатив.
