Понятие графа. Подграф графа. Компонента связности графа. Точка сочленения. Дерево. Паросочетание. Гамильтонов цикл и гамильтонов граф. Взвешенный граф.
Граф задается двумя множествами: непустым множеством X и множеством U, содержащим пары элементов из множества X. Граф, заданный на множествах Х и U, обозначается G=(X,U). Если элементы в парах U не упорядочены, то граф называется неориентированным, в противном случае – ориентированным, или орграфом. Элементы множества X называют вершинами графа, а множества U – ребрами для неориентированного графа и дугами для орграфа. На плоскости граф задается в виде точек (вершин) и линий, соединяющих некоторые из них (ребер или дуг).
Подграфом графа G называется граф G1 с множеством вершин Х1 и множеством ребер U1 такой, что Х1 ∈ X, U1 ∈ U.
Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа.
Вершина графа, удаление которой повышает число компонент связности, называется точкой сочленения. Под удалением вершины понимается удаление самой вершины и всех инцидентных ей ребер.
Деревом называется связный граф без циклов.
Регулярный граф, все вершины которого имеют степень 1, называется паросочетанием.
Гамильтоновым циклом называется гамильтоновая цепь, начало и конец которой совпадают. Граф называется гамильтоновым, если в нем имеется гамильтонов цикл.
Граф называется взвешенным, если каждому его ребру, или каждой вершине, или и тем и другим поставлено в соответствие некоторое число, называемое весом.
Ориентированный граф. Путь и длина пути в графе. Элементарный путь и контур. Заходящие и исходящие дуги. Полустепень исхода и полустепень захода вершины. Матрица смежности графа. Матрица инциденций. Сеть. Двухполюсная транспортная сеть, условия ее существования.
Для ориентированных графов в основном все определения сохраняются, однако имеются некоторые отличия. Последовательность дуг, в которой конец предыдущей дуги совпадает с началом следующей, называется путем. Длина пути определяется количеством в нем дуг. Путь называется простым, если в нем дуга не встречается дважды, в противном случае он является составным.
Путь, в котором никакая вершина не встречается дважды, называется элементарным. Путь, который начинается и заканчивается в одной и той же вершине, называется контуром.
Для ориентированного графа вместо степени вершины вводится понятие полустепеней исхода и захода. Если вершина является началом дуги, то дуга называется исходящей из вершины, если концом, то – заходящей. Полустепенью исхода вершины d – (x) называется число дуг, исходящих из этой вершины, полустепенью захода d+(x) – число дуг, заходящих в вершину.
При решении задач на компьютере граф лучше представлять в виде матриц, операции с которыми удобно проводить на компьютере. Известно несколько типов матриц, позволяющих задавать граф: смежности, инциденций, пропускных способностей.
Сетевой график (сеть) - это связный взвешенный ориентированный граф без петель и контуров.
При построении сетевого графика необходимо соблюдать ряд правил:
1. В сетевом графике рекомендуется иметь одно исходное и одно завершающее событие (по аналогии с рассмотренным ранее понятием сети). Если это не так, то необходимо вводить фиктивные события и работы .
2. В сетевом графике не должно быть «хвостовых» событий (кроме исходного), которым не предшествует хотя бы одна работа. Обнаружив в сети такое событие, необходимо определить исполнителей предшествующих им работ и включить эти работы в сеть.
3. В сетевом графике не должно быть «тупиковых» событий, т.е. событий, из которых не выходит ни одна работа, за исключением завершающего события.
4. В сетевом графике не должно быть циклов, контуров и петель. При возникновении циклов и контуров, что довольно часто встречается в сложных сетях, необходимо вернуться к исходным данным и путем пересмотра состава работ добиться их устранения.
5.Любые два события должны быть связаны не более чем одной работой-стрелкой. То есть, не должно быть параллельно выполняемых работ. Они или объединяются или вводятся фиктивные события и работы, которые изображаются на сетевом графике пунктиром.
Понятие и предмет теории массового обслуживания. Составляющие СМО: каналы, заявки и процедуры обслуживания. Однородные каналы СМО. Фаза обслуживания.
Каждая система массового обслуживания (СМО) состоит из определенного числа обслуживающих единиц (станков, приборов, компьютеров, машин, работников и т.д.), которые называются каналами обслуживания. По количеству каналов СМО подразделяют на одноканальные и многоканальные системы.
СМО делятся на два основных класса:
1. СМО с отказами. Заявка, поступающая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем в процессе обслуживания не участвует. Примером СМО с отказами служит телефонная сеть, в которой заявка на телефонный разговор покидает СМО в том случае, когда соответствующий канал занят.
2. СМО с ожиданиями (очередью). Заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание. СМО с ожиданием подразделяются на разные виды в зависимости от того, как организована очередь: с ограниченной или неограниченной длиной ожидания, с ограниченным временем ожидания и т.д. Большое значение для классификации СМО имеет дисциплина обслуживания, определяющая порядок выбора заявок из числа поступивших и порядок распределения их между свободными каналами. По этому признаку обслуживание заявок может быть организовано по принципу «первый пришел – первый обслужен» или по принципу «первый пришел – последний обслужен» (такой порядок обслуживания характерен при отгрузке однородной продукции со склада). Кроме перечисленных дисциплин обслуживания следует отметить обслуживание с приоритетом. При этом приоритет может быть абсолютным, когда более важная заявка вытесняет из обслуживания обычную заявку или относительным, когда важная заявка получает лишь лучшее место в очереди. Заявки клиентов на обслуживание в СМО поступают, как правило, не регулярно, а случайно, образуя так называемый поток заявок (или требований). Процесс работы СМО также носит случайный характер, т.е. представляет собой случайный процесс.
Под случайным (стохастическим, вероятностным) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностным законом.
Процесс называется процессом с дискретными состояниями, если его возможные состояния S1, S2, S3, ..., Sn, ... можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно.
Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а являются случайными.
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это означает, что состояние СМО меняется скачком в случайные моменты появления каких- либо событий (появление новой заявки, приоритета обслуживания, окончания обслуживания).
Случайный процесс называется марковским, или случайным процессом без последствий, если для любого момента времени tо(t нулевое) вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент tо и не зависят от того, когда и как система пришла в это состояние. Если процесс функционирования СМО является марковским, то анализ ее функционирования существенно упрощается.
Приведем пример марковского процесса.
Пусть S – счетчик пройденного автомобилем расстояния. Состояние системы в момент t характеризуется числом километров, пройденных автомобилем до данного момента. Допустим, что в момент времени tо счетчик показывает Sо. Тогда вероятность того, что в момент t > to счетчик покажет то или иное число километров S1, зависит только от Sо, но не зависит от того, каким были показатели счетчика до момента tо. В ряде случаев предысторией рассматриваемых процессов можно пренебречь и применять для их изучения марковские модели. При анализе случайных процессов с дискретным состоянием удобно пользоваться так называемым графом состояний. Обычно состояния системы обозначаются вершинами ориентированного графа, а возможные переходы из состояния в состояние ориентированными дугами, соединяющими вершины.
Пример. Построим граф состояний следующего случайного процесса: устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное случайное время. Для того чтобы решить эту задачу, перечислим возможные состояния системы:
So – оба узла исправны;
S1 – первый узел ремонтируется, второй исправен;
S2 – первый узел исправен, второй ремонтируется;
S3 – оба узла ремонтируются (см. рис. 1).
Дуга, направленная из So в S1 означает переход в момент отказа
первого узла; из S1 в So – переход в момент окончания ремонта этого узла.
На графе отсутствуют стрелки из So в S3 и из S1 в S2. Это объясняется
тем, что выходы узлов из строя предполагаются независимыми друг от друга
и вероятностью одновременного выхода из строя двух узлов (переход от So в
S3) или одновременного окончания ремонтов двух узлов (переход из S3 в So)
можно пренебречь.
Рис. 1. Пример
графа состояний системы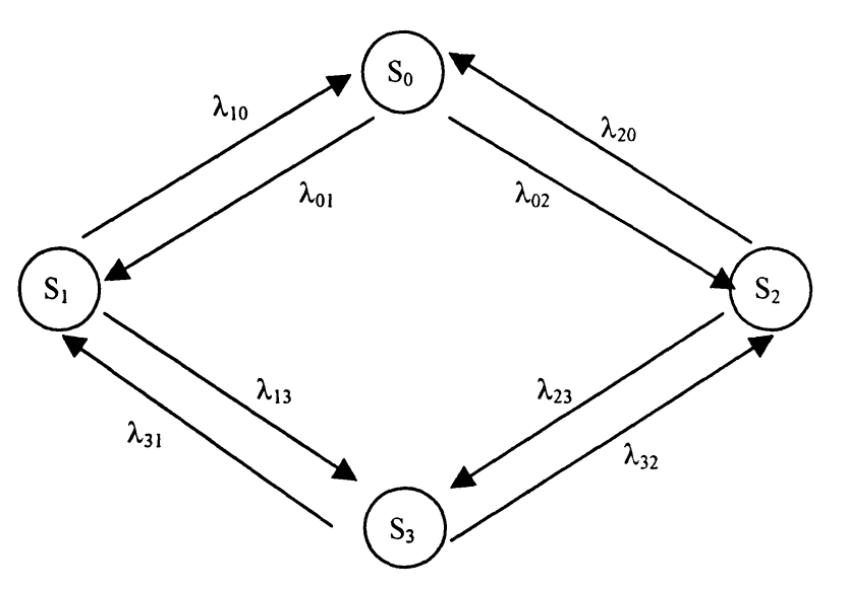
Потоки событий. Регулярность и стационарность потоков. Потоки без последействия. Ординарность потоков. Пуассоновский поток событий. Формула Пуассона для вычисления вероятности события.
Процесс поступления в систему массового обслуживания заявок является вероятностным. Он предоставляет собой поток однородных или неоднородных событий, поступающих через случайные промежутки времени (например, поток вызовов на телефонной станции, поток отказов компьютеров, поток покупателей и т.д.). Поток характеризуется интенсивностью λ – частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.
Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени.
Например, поток изделий на конвейере сборочного цеха в том случае, если он движется с постоянной скоростью, является регулярным.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока есть величина постоянная λ (t) = λ. Поток автомобилей на городском проспекте не является стационарным в течение суток, но его можно считать стационарным в течение какого-то временного интервала, например, в часы пик. В этом случае, хотя количество автомобилей, проходящих в единицу времени, будет различным в разные часы, их среднее число будет постоянным и не будет зависеть от времени.
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени τ1 и τ2 – число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
Например, поток пассажиров, входящих в метро, практически не имеет последействия. А поток покупателей, отходящих от кассы с покупками, уже имеет последействие. Это следует из того, что интервал времени между отдельными покупателями не может быть меньше, чем минимальное время обслуживания каждого из них.
Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени Δt двух и более событий пренебрежительно мала по сравнению с вероятностью попадания одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами.
Например, поток поездов, подходящих к станции, ординарен, а поток вагонов неординарен. Вероятность того, что событие произойдет один раз на интервале Δt для ординарного потока пропорциональна dt и равна λ dt.
Поток событий называется простейшим, если он одновременно стационарен, ординарен и не имеет последствий. Определим распределение вероятностей для такого потока (т.е.найдем величины pn (τ), n = 0, 1,...,k).
Для любого промежутка времени τ имеем:
P0 (τ) + p1 (τ) +…+ pk (τ) +…= 1. (1)
Кроме того, для промежутка Δt
p0 (Δt) + p1 (Δt) +…+ pk (Δt) +…= 1. (2)
Но, по предположению об ординарности при Δt → dt величины
pk (Δt), k = 2, 3,... – бесконечно малые по сравнению с Δt, поэтому
p0 (dt) + p1 (dt) = 1. (3)
Так как
p1 (dt) = λ dt, то p0 (dt) = 1 – λ dt. (4)
Теперь вычислим вероятность pn (τ + dt) того, что в интервале τ + dt произойдет n событий Е. Для того чтобы в интервале τ + dt событие Е произошло n раз, должен осуществиться один из взаимоисключающих
случаев:
а) n событий Е в интервале τ и 0 событий Е в интервале dτ, следующем непосредственно за τ , вероятность этого случая равна pn (τ) (1 – λ dτ);
б) (n – 1) событий Е в интервале τ и 1 событие в интервале dτ, соответствующая вероятность равна pn – 1(τ) (1– λ dτ).
Таким образом, по формуле полной вероятности
pn (τ + dt) = pn (τ) (1 – λ dτ) + pn – 1(τ) (1 – λ dτ) + 0(dτ), (5)
где 0(dτ) – бесконечно малые высшего порядка по сравнению с dτ.
pn (τ + dt) – pn (τ) = – λ pn (τ) dτ + λ pn – 1(τ) dτ, (6)
или
(pn (τ + dτ) – pn (τ))/ dτ = d pn (τ)/ dτ – λ pn (τ) + λ pn – 1(τ) = – λ [ pn (τ) – pn – 1(τ) ] , (7)
где n = 1, 2,…
Если n = 0, то из (7) с учетом того, что pn – 1(τ) = 0, получим
d pn (τ)/ dτ = p0 (τ) = – λ p0 (τ) . (8)
Дифференциальные уравнения (7), (8) описывают состояния простейшего потока.
Дополним их очевидными начальными условиями:
p0 (0) = 1, pn (0) = 1, n = 1, 2,… (9)
Решая (8) с учетом (9), получим
p0 (τ) = е – λτ . (10)
Для нахождения решения системы (7) используем преобразование
Лапласа-Карсона. Для этого положим
ψn (S) = L { pn(τ) } = S ∫ 0бескpn(τ) е – S τ dτ, n = 0, 1,…
Применив это преобразование к (7), приходим к системе
алгебраических уравнений
S ψn (S) = – λ [ψn (S) – ψn – 1 (S)] или ψn (S) = λ/(λ + S) ψn – 1 (S)
Так как ψn (S) = λ/(λ + S) то
ψ1 (S) = λ /(λ + S) ψ0 (S) = λ S/ (λ + S)2
ψ2 (S) = λ2/(λ + S )3 ,…, ψn (S) = λn S/(λ + S) n + 1
Используя таблицы соответствий преобразования Лапласа, найдем окончательно:
p0 (τ) = е – λt ; p1 (τ) = λ τ е – λt / 1! ,…, pn (τ) = (λ τ)n e – λt/ n!
Как видим, нами получено распределение Пуассона, причем величина
λ τ есть среднее число событий Е в интервале τ .
Таким образом, ординарный поток заявок без последействий описывается распределением (законом) Пуассона. Следует отметить, что простейший поток в теории массового обслуживания играет такую же роль, как и нормальный закон в теории вероятностей. Главная его особенность заключается в том, что при сложении нескольких независимых простейших потоков образуется суммарный поток, который также близок к простейшему.
Непосредственной подстановкой получаем
pn + 1(τ)/ pn (τ )=λ τ /n + 1 или pn + 1(τ) = (λ τ/ n + 1) pn(τ)
Процесс многократного появления однородных событий Е через случайные интервалы времени при выполнении условий стационарности, ординарности и отсутствия последействия называется процессом Пуассона.
Найдем распределение интервала времени Т между произвольными двумя соседними событиями простейшего потока. В соответствии с (10) вероятность того, что на участке времени длиной t не появится ни одного из последующих событий, равна
p (T ≥ t) = e – λt , а вероятность противоположного события, т.е. функция распределения случайной величины Т, есть F(t) = p(T < t) = 1 – e – λt . (18)
Плотность вероятности случайной величины есть производная ее функции распределения (рис. 2), т.е. φ (t) = F′(t) = λ e – λt . (19)
Распределение, задаваемое плотностью вероятности (19) или функцией распределения (18), называется показательным, или экспоненциальным. Таким образом, интервал времени между двумя соседними произвольными событиями имеет показательное распределение, для которого математическое ожидание равно среднему квадратичному
отклонению случайной величины и обратно по величине интенсивности
потока λ :
а =1/ λ (20)
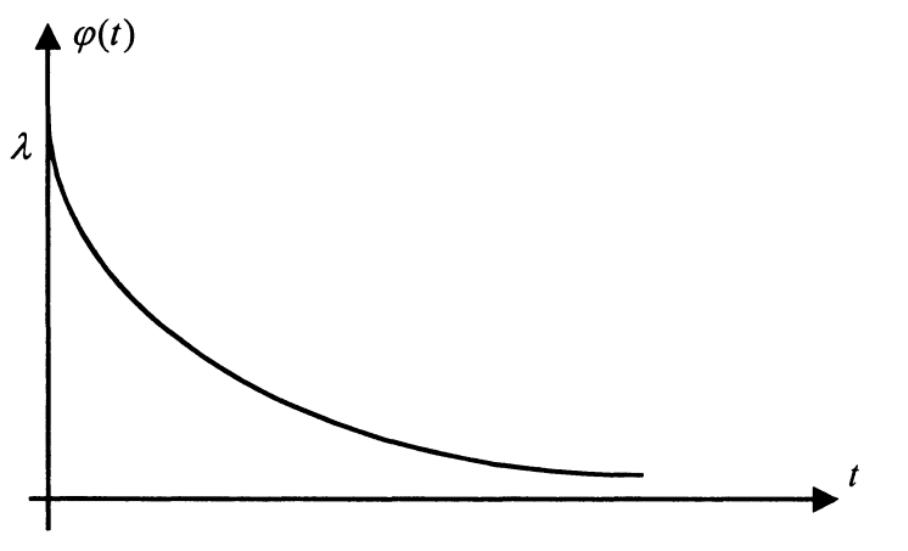
Рис. 2. Плотность вероятности случайной величины φ (t) = λ e – λt
Важнейшее свойство показательного распределения состоит в следующем: если промежуток времени, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части промежутка (Т – τ): он будет таким же, как и закон распределения всего промежутка Т. Для простейшего потока с интенсивностью λ вероятность попадания на элементарный (малый) отрезок времени Δt хотя бы одного события потока равна, согласно (18),
pΔt = p(T < Δt) = 1 – e – λΔt ≈ λ Δt.