0. экстраполяции

1. интерполяции

2. теорема Котельникова.

   Допустимая погрешность оценивается в равномерной и среднеквадратической метриках.

   1. Постановка задачи.

   Непрерывные сигналы в системе обобщенных координат Х,Т описываются непрерывными функциями x(t). Переход от аналогового представления сигнала к цифровому может дать больше преимущества при передаче, хранении и обработке информации. Этот переход связан с дискретизацией сигнала по уровню Х и по времени Т.

   В результате дискретизации по времени сигнал непрерывного аргумента f(t) заменяется сигналом f(t_i) дискретного аргумента

   , где - шаг дискретизации.

   По множеству мгновенных значений сигнала f(t_i) выполняется восстановление аналогового сигнала в виде его оценки:

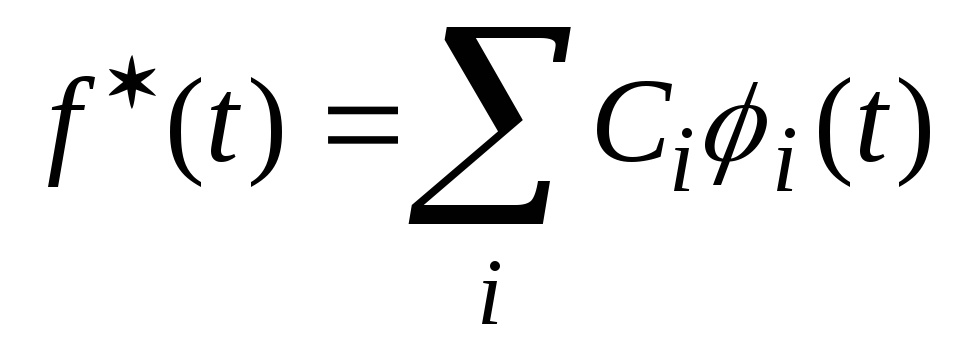   , где C_i - коэффициенты разложения

   - базисные функции.

   Когда исходный сигнал представляется в виде выборок, т.е. подвергается дискретизации,

   C_i= f(t_i).

   Погрешность e, возникающая в результате замены сигнала f(t) åãî оценкой f^*(t) – это погрешность дискретизации. Используются два вида показателей точности дискретизации:

   - равномерный 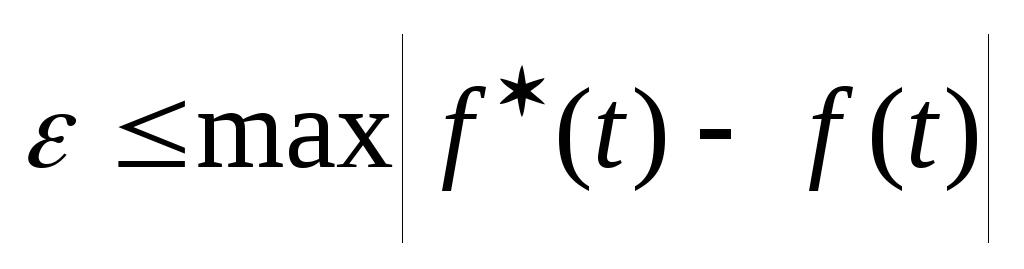(1)

   - среднеквадратический 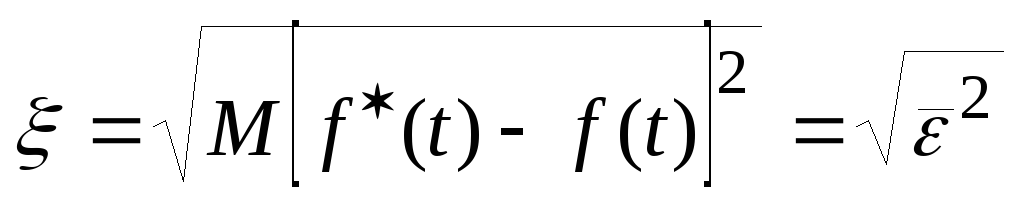(2)

   (М – знак математического ожидания).

   Для восстановления дискретизированных сигналов используются способы с интерполяцией и экстрополяцией. В качестве восстанавливающих функций применяют: ряд Котельникова, ряд Фурье, полиномы Чебышева, Лежандра, Уолша и степенные полиномы.

   Интерполяционный способ восстановления осуществляется чаще всего с помощью интерполяционного полинома Лагранжа:

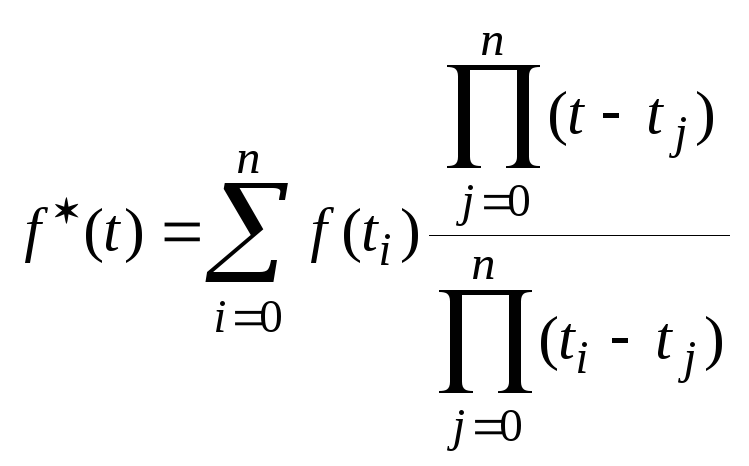   (3)

   где n – степень полинома

   t₀; t_i; t_j – узлы интерполяции.

   Способ с экстраполяцией осуществляется с помощью ряда Тейлора:

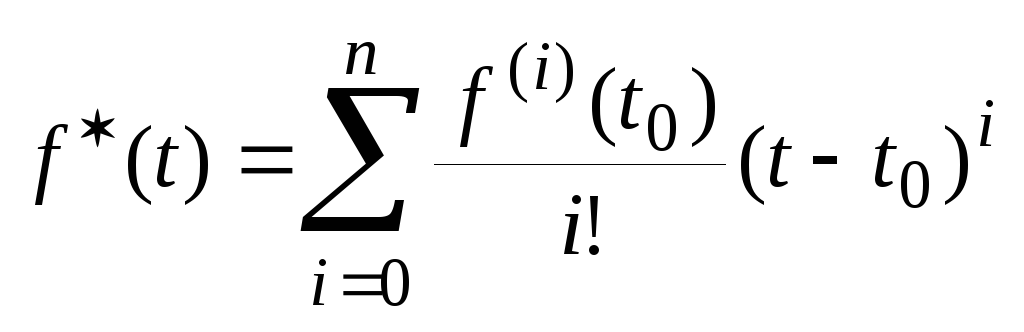   (4)

   В соответствии с заданием приведем также ряд Котельникова, который теоретически может быть использован для восстановления дискретизированного сигнала:

   (5)

   где к – номер отсчета (дискрета времени)

   DТ – интервал (шаг) дискретизации

   Fm – максимальная частота спектра сигнала.

   При любом из рассмотренных способов восстановления сигнала существенным является выбор величины шага дискретизации DТ. При большой величине DТ падает точность дискретизации. При малой его величине возникает избыточность информации, которая ведет к усложнению аппаратуры. Величину шага дискретизации DТ выбирают по допустимой погрешности дискретизации e.

   Ниже бедет показано, что для определения величины DТ по допустимой величине e используются производные от корреляционной функции сигнала и величина наибольшей частоты Fm (полосы частот) спектра сигнала.

   Нам задана корреляционная функция сигнала

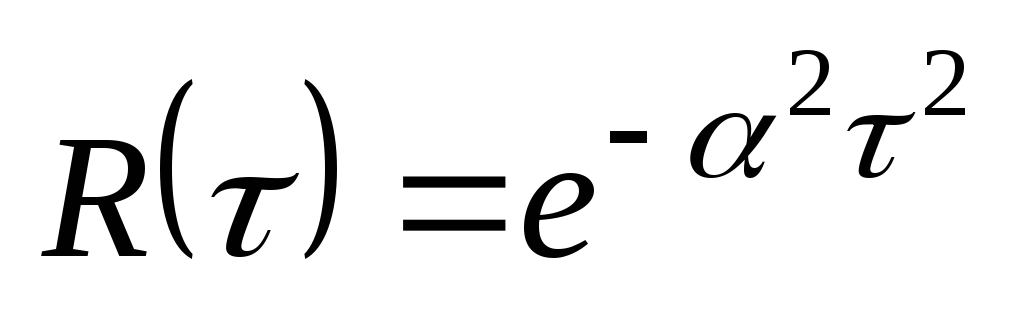   (6)

   Данные же о максимальной частоте (полосе частот) спектра отсутствуют.

   Для определения Fm по заданной корреляционной функции можно использовать теорему Винера-Хинчина

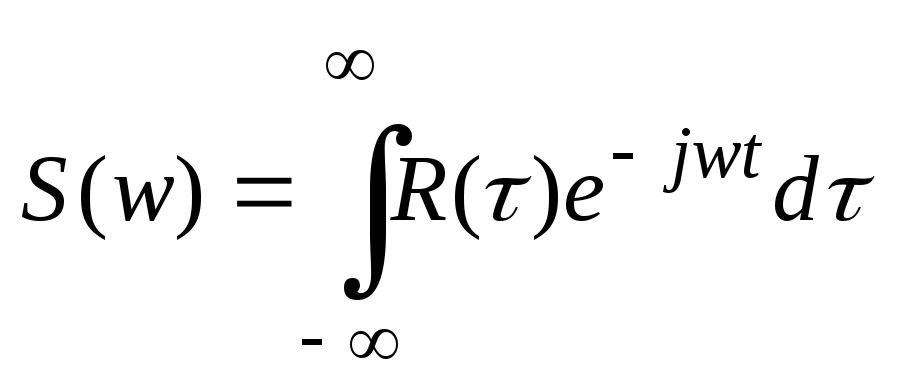   (7)

   где S(w) – спектральная плотность мощности сигнала.

   При этом подходе следует вычислить спектральную плотность мощности S(w). Затем вычисляется полная мощность сигнала, как

   (8)

   и, наконец, определяется полоса w_m спектра сигнала из

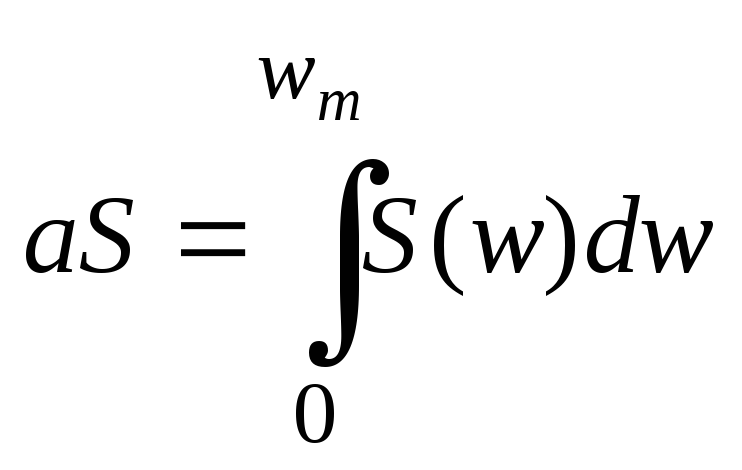   (9)

   где a – значимый уровень, например a=0,9 èëè 0,99.

   В этом варианте задача усложняется тем, что при определении S(w) èç (7):

   

   интеграл не выражается в элементарных функциях и может быть определен только численно.

   Удобнее использовать разработанный в теории измерительной техники метод Железнова . Сущность метода в следующем. Метод позволяет установить связь между корреляционной функцией стационарного случайного процесса и так называемой эффективной полосой частот сигнала. Метод Железнова справедлив для случайных процессов у которых корреляционная функция имеет ограничение: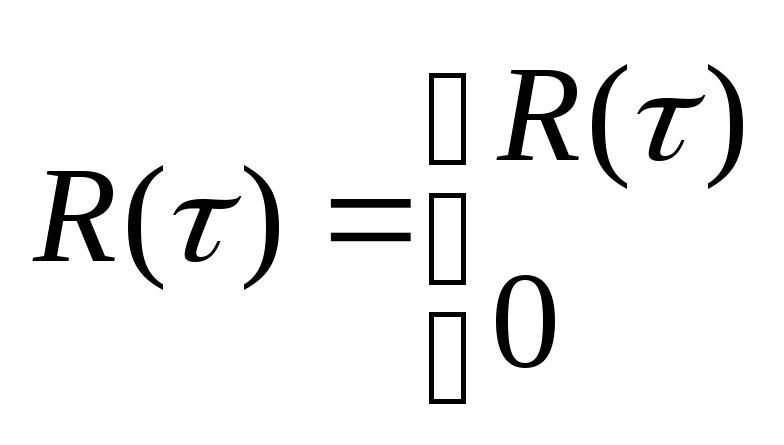

   (10)

   где t₀ – интервал корреляции.

   Это означает, что соседние значения непрерывного сигнала f(t₁) и f(t₂) отсчитанные через промежуток 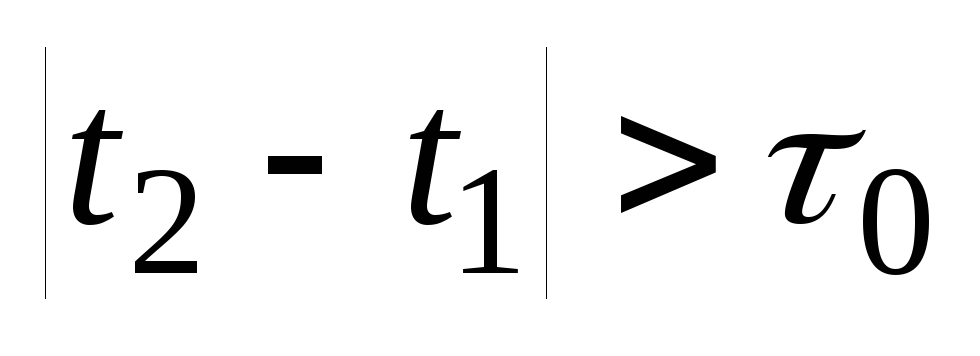, могут считаться независимыми. В этом методе вводится понятие эффективной полосы частот сигнала Dw_эфф ,определяемой по его спектральной плотности (рис.1):

   Dw_эфф=

   В этом методе

   Df_эфф= 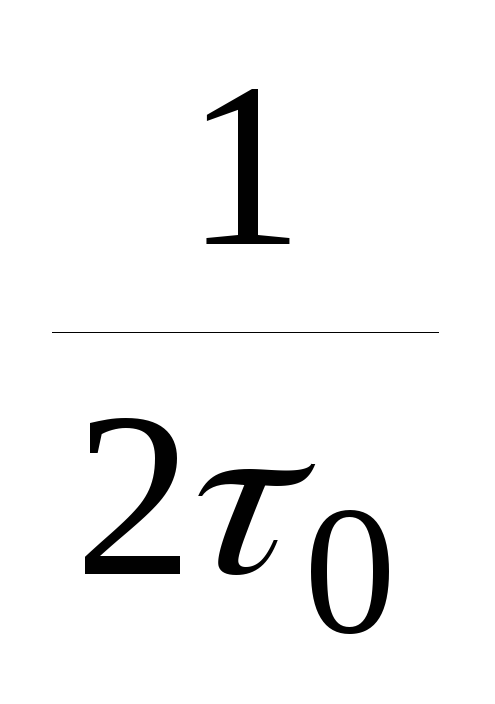или Dw_эфф=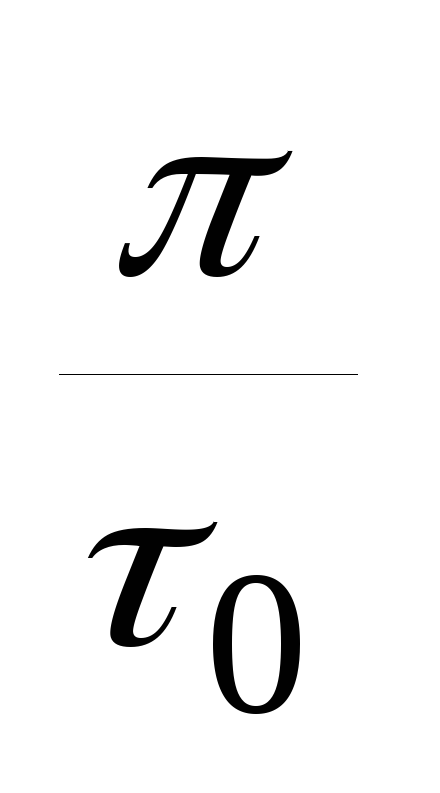 (11)

   Определим по методу Железнова полосу частот спектра заданного ССП.

   Заданная функция корреляции может считаться удовлетворяющей условию (10). Это видно из графиков (рис. 2) для функции

   

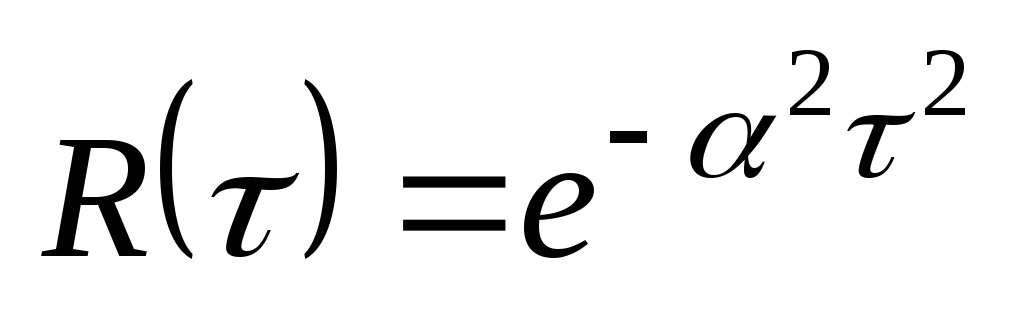
   Зададим порог, при котором будем считать R(t)=0

   

   и решим это уравнение относительно t

   

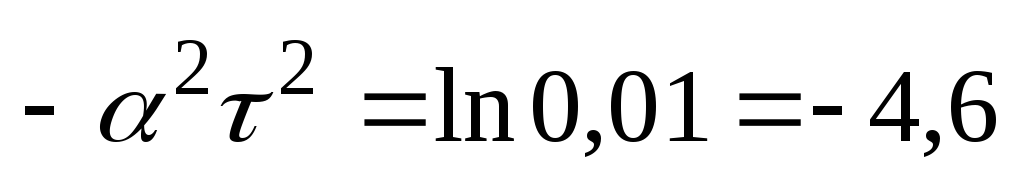
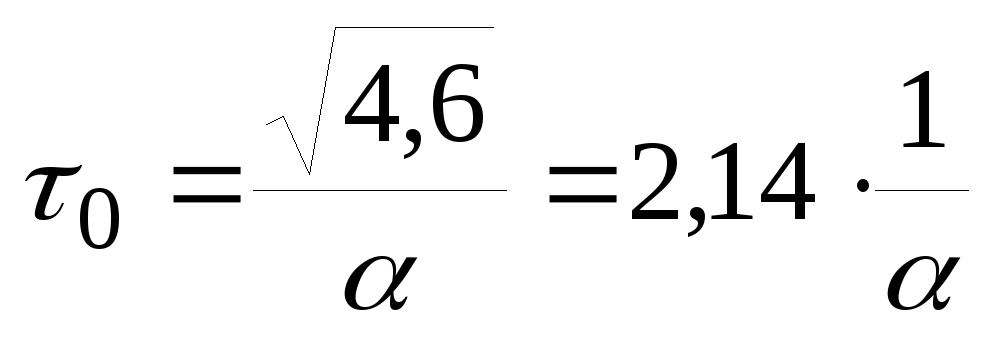   (12)

   Из (11) и (12):

   Dw_эфф==1,46a (13)

   Выбор эффективной полосы таким способом вносит погрешность дополнительно к погрешности дискретизации. Поэтому примем полосу частот спектра в виде:

   w_m=1,46ba (14)

   где b>1.

   2. Определение шага дискретизации при восстановлении сигнала интерполяцией.

   2.1. Равномерный показатель точности дискретизации.

   2.1.1. Интерполяция полиномом нулевой степени

   Из выражения интерполяционного полинома Лагранжа (3) для n=0 при t=t_k ,т.е. на к-том узле дискретизации, расположенном в начале интервала дискретизации:

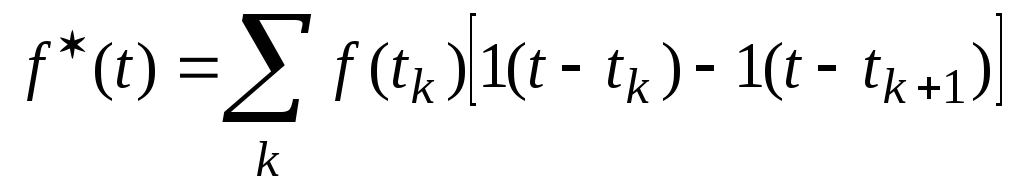   (15)

   Оценка максимальной погрешности интерполяции:

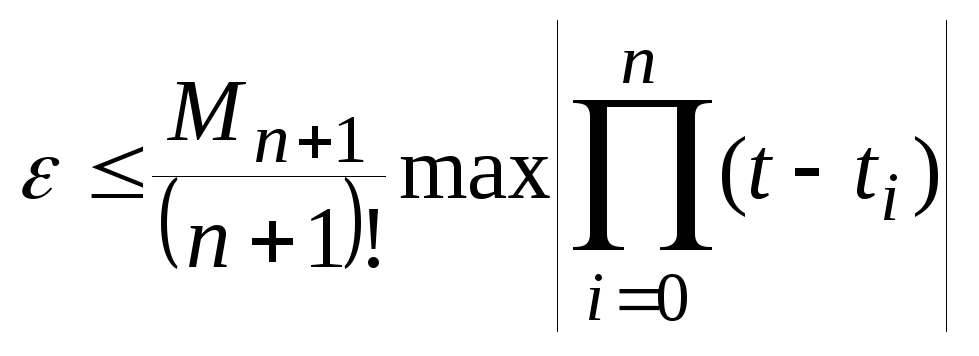   (16)

   где M_n+1 – максимум модуля (n+1)^й производной сигнала.

   При n=0 максимальная погрешность на к-том интервале

   

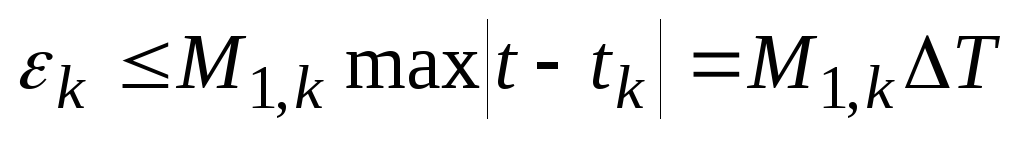
   Максимальная погрешность на всем интервале задания сигнала:

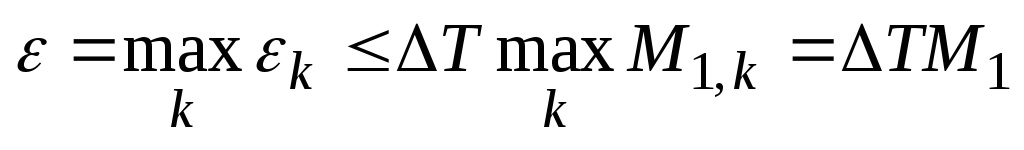   (17)

   где М₁ – максимум модуля 1^-ой производной сигнала на всем интервале.

   Из (17) шаг дискретизации:

   (18)

   Значение М₁ для заданного сигнала неизвестно. Оценка М₁ определяется с помощью неравенства Бернштейна:

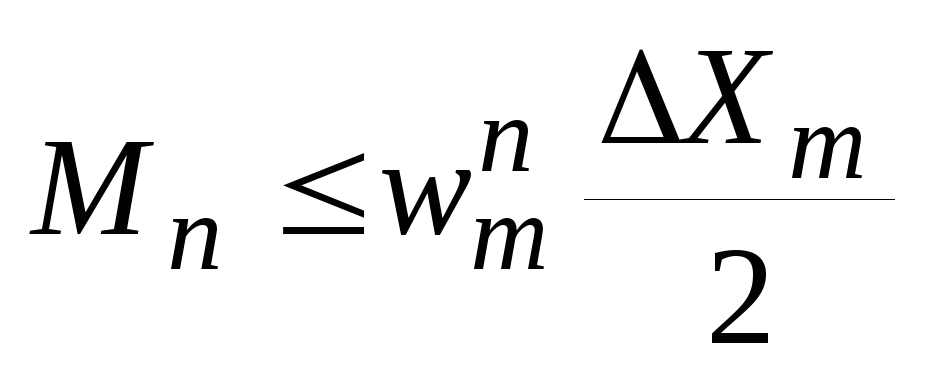   ,где w_m=2pFm – ширина спектра сигнала

   DX_m – диапазон изменения сигнала

   Тогда при n=0 из (18) и (19)

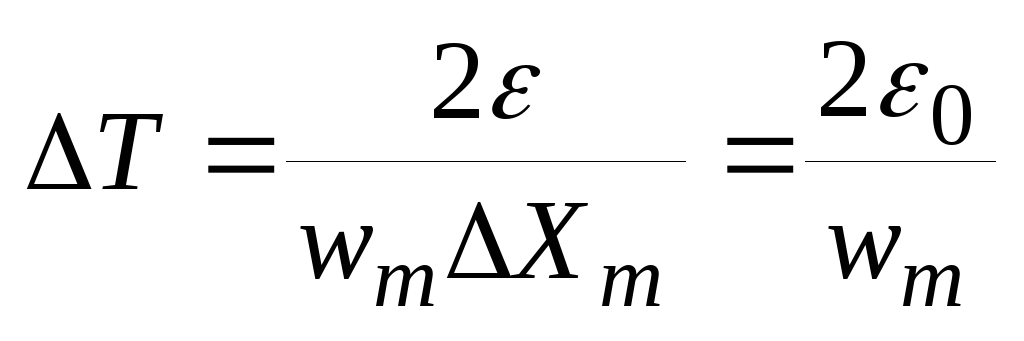   (20)

   где - нормированная погрешность восстановления.

   Для заданного сигнала из (20) и (14)

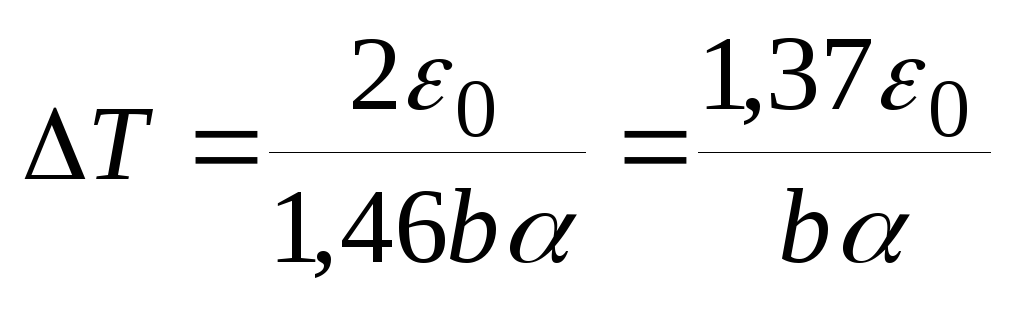   (21)

   2.1.2. Интерполяция полиномом первой степени.

   Из (3) для n=1 оценка сигнала имеет вид:

   

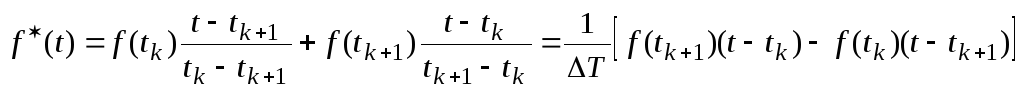
   где

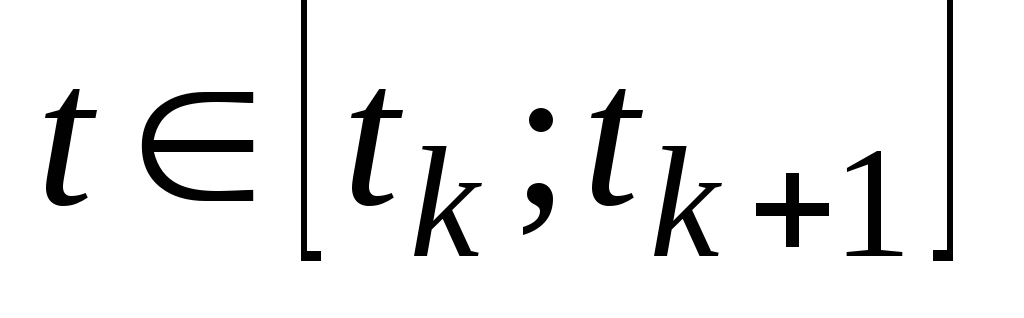
   На рис.4 показано восстановление сигнала интерполяцией с n=1.

   Из (16) погрешность восстановления на интервале :

   

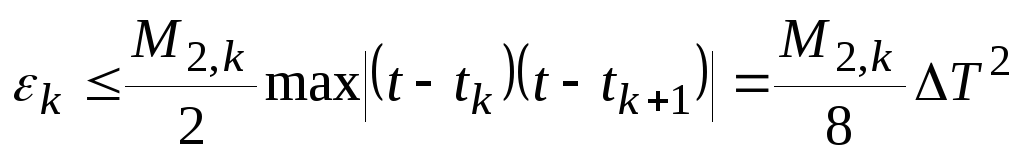
   и на всем интервале восстановления

   

   Откуда

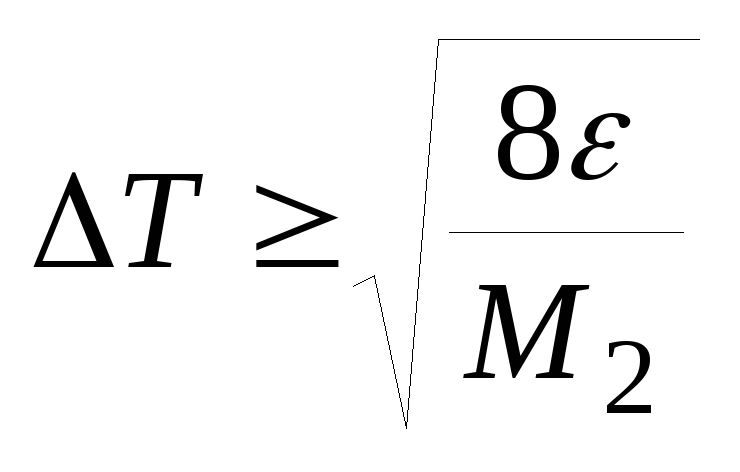   (22)

   Из неравенства Бернштейна (19)

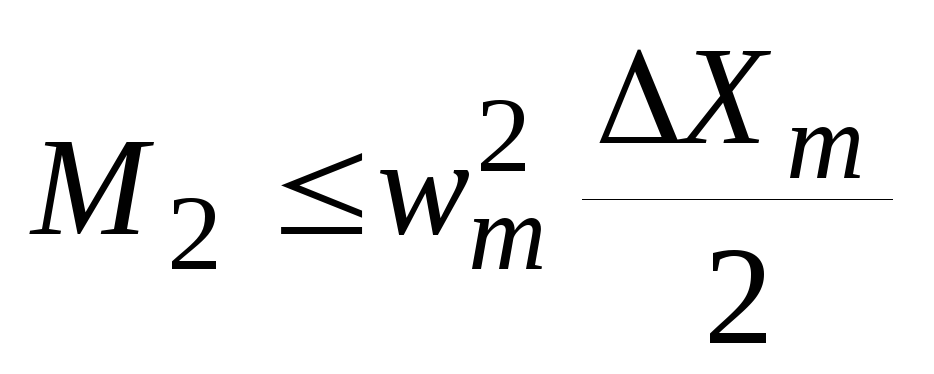   (23)

   С учетом (23):

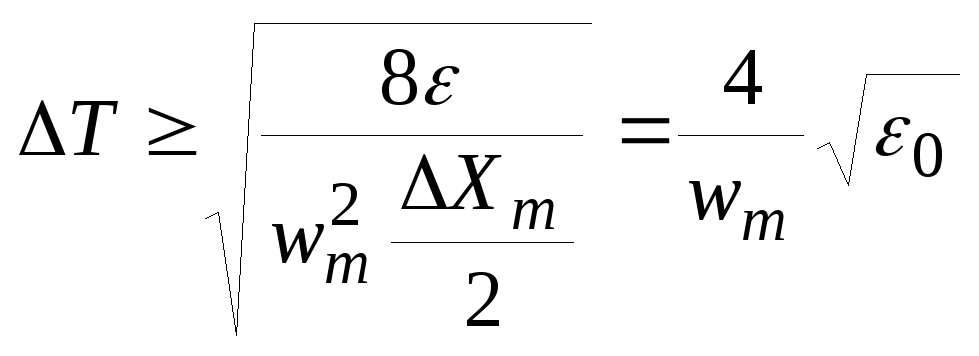   (24)

   где 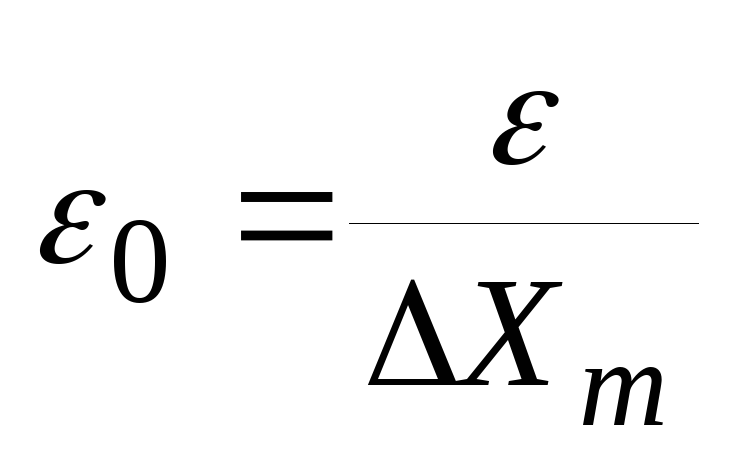- нормированная погрешность восстановления.

   Для заданного сигнала шаг дискретизации с учетом (14)

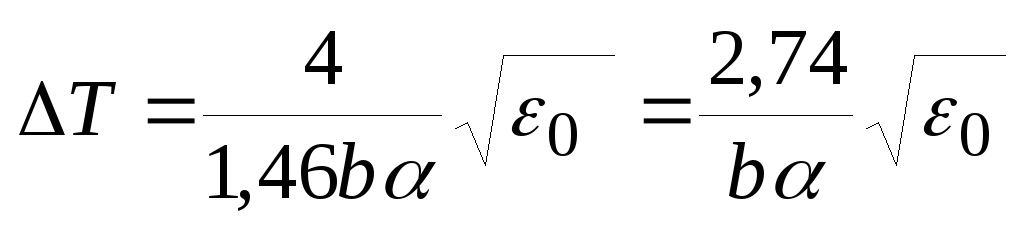   (25)

   2.2. Среднеквадратический показатель точности дискретизации.

   2.2.1. Интерполяция полиномом первой степени.

   Текущая погрешность восстановления (см.рис 3)

   

   где

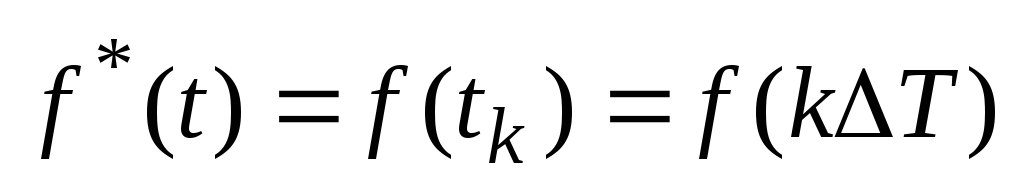
   Ссредняя квадратическая погрешность восстановления определяется усреднением по множеству реализаций как

   

   В показано, что для дифференцируемого сигнала шаг дискретизации определяется как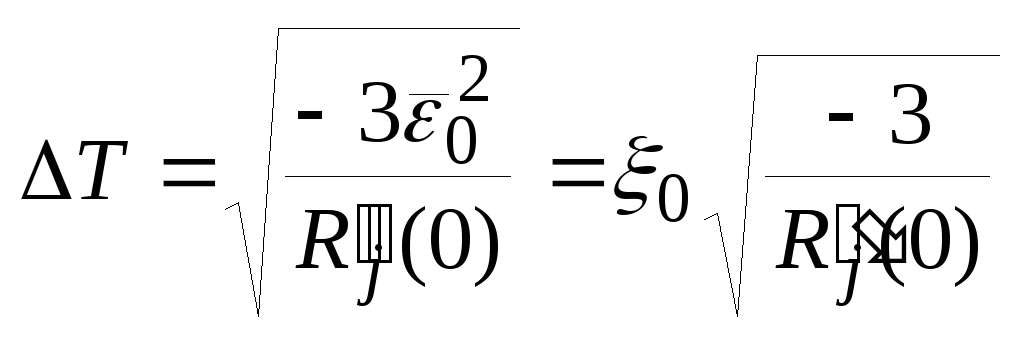

   (26)

   где

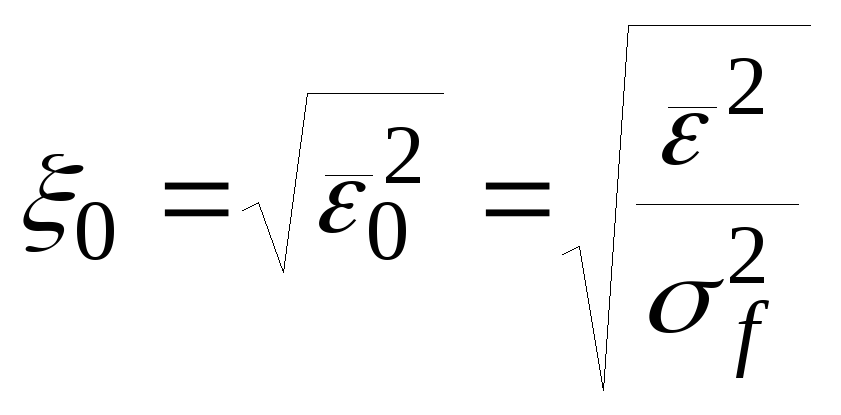
   R_f – нормированная корреляционная функция сигнала

   s_f² – дисперсия сигнала

   Условием дифференцируемости случайного сигнала, является равенство нулю 1^-îé производной его корреляционной функции при t=0.Проверим это условие.

   

   

   

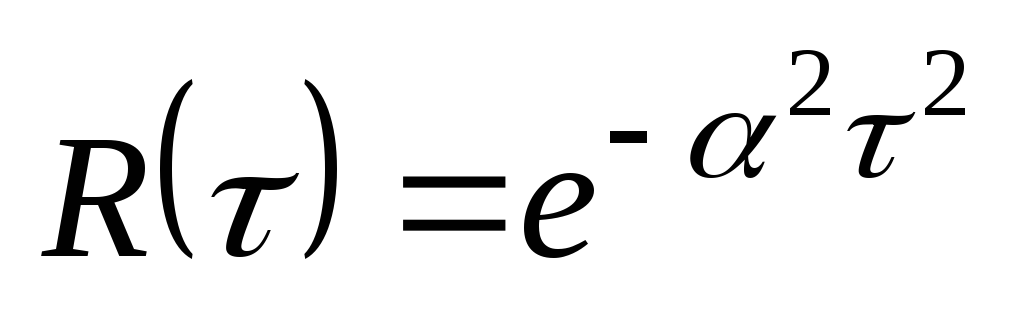
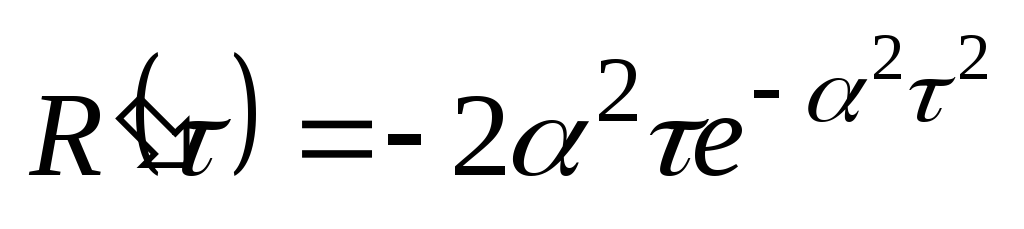
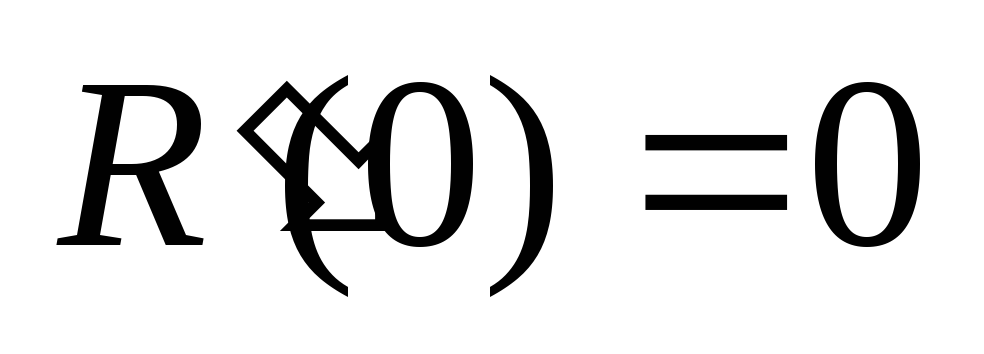
   т.е. заданный сигнал является дифференцируемым.

   Определяем 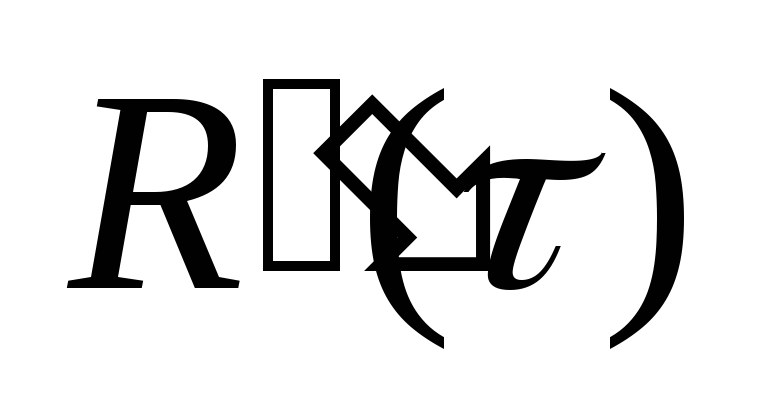для подстановки в (26):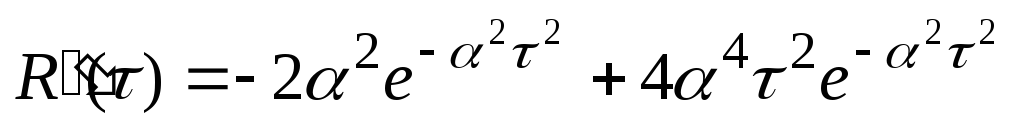

   

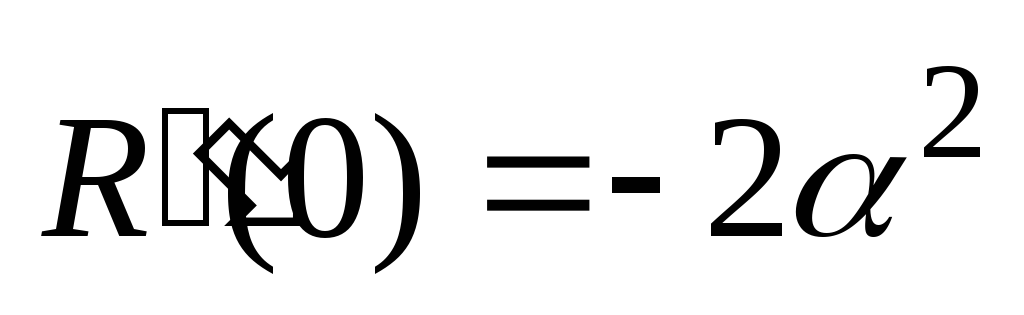   (27)

   Шаг дискретизации получаем из (26) и (27)

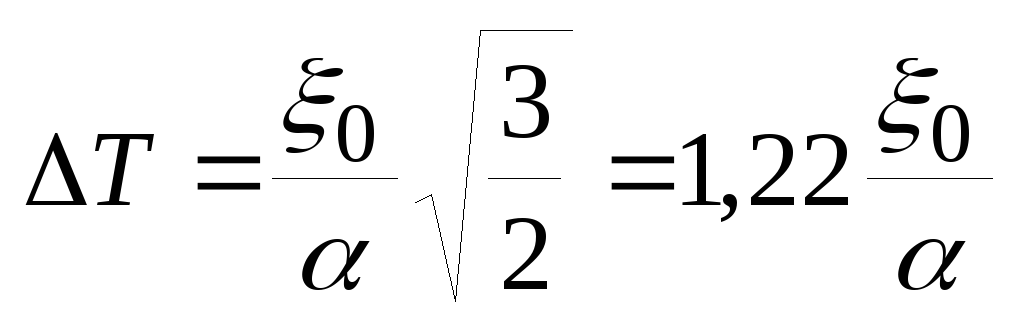   (28)

   2.2.2. Интерполяция полиномом первой степени.

   В приведено выражение для шага дискретизации при интерполяционном восстановлении сигнала полиномом 1^-ой степени при степени дифференцирующего сигнала m=1.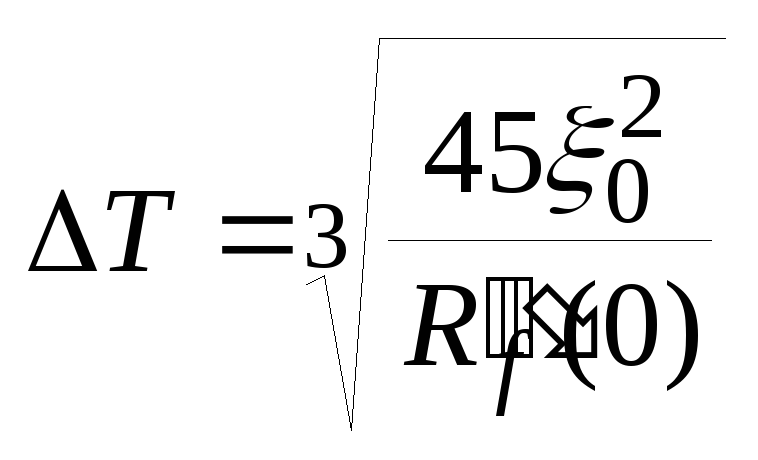

   (29)

   Находим 3^ю производную от заданной корреляционной функции:

   т.е.

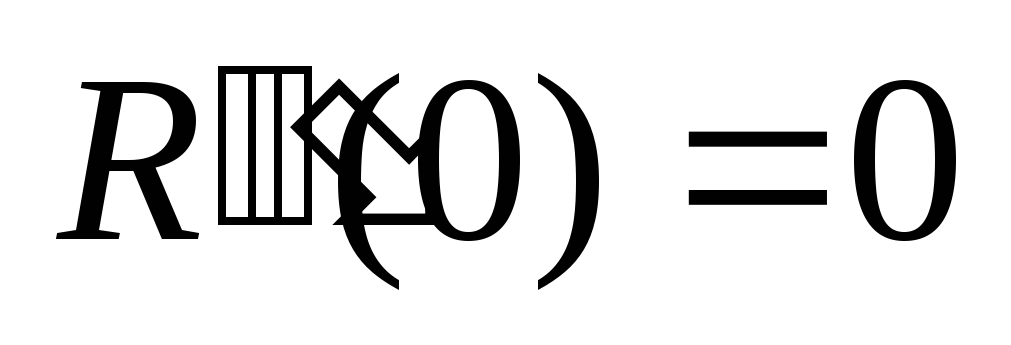
   В этом случае не удается оценить шаг аппроксимации в зависимости от среднеквадратической ошибки.

   3. Определение шага дискретизации при восстановлении сигнала экстрополяцией.

   3.1. Равномерный показатель точности дискретизации.

   3.1.1. Экстрополяция полиномом нулевой степени.

   т.к. экстрополяция осуществляется рядом Тейлора:

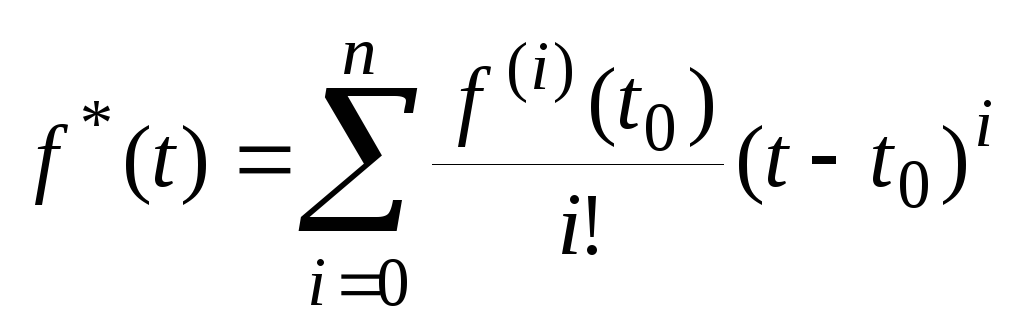   (30),

   то при n=0 для к-ого узла 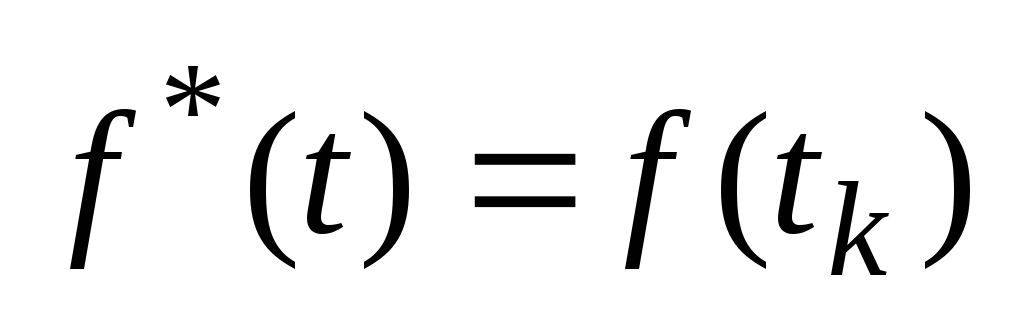и разницы с интерполяцией полиномом нулевой степени нет (см. п.2.1.1.). Поэтому и в случае экстрополяции имеем шаг дискретизации, согласно (21):

   

   3.1.2. Экстрополяция полиномом 1^-ой степени.

   В случае линейной экстрополяции (n=1) оценка сигнала на интервале 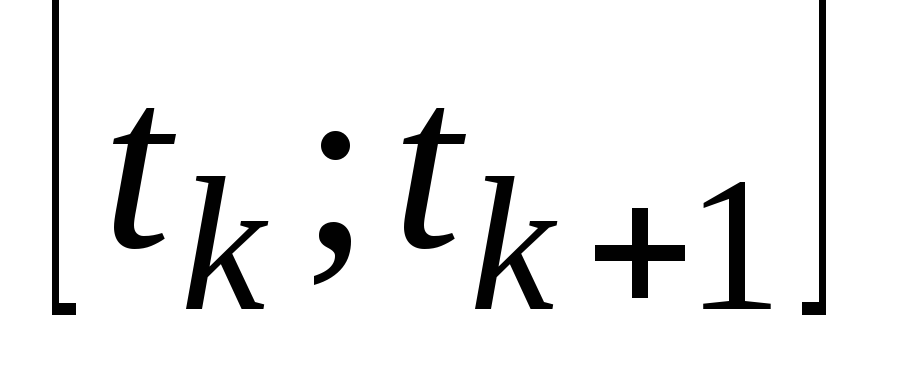, согласно (30) имеет вид: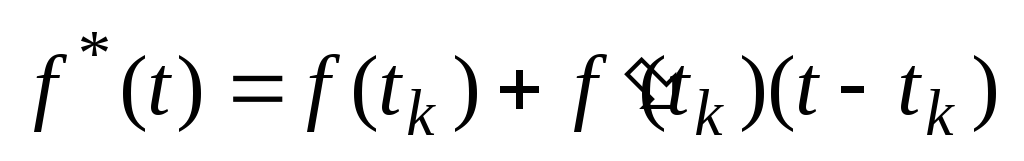

   

   Пример линейной экстрополяции показан на рис.5.

   Ошибка экстрополяции на к-том интервале из (16):

   

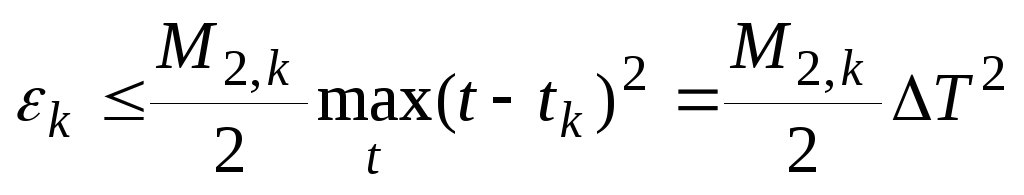
   На всем интервале восстановления

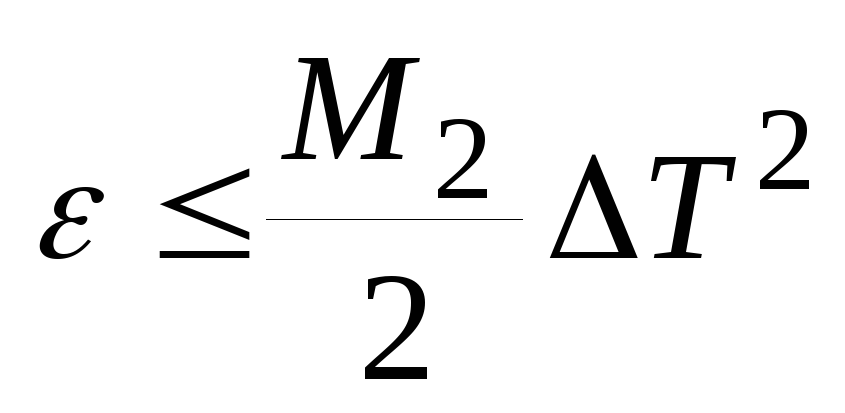   и шаг дискрретизации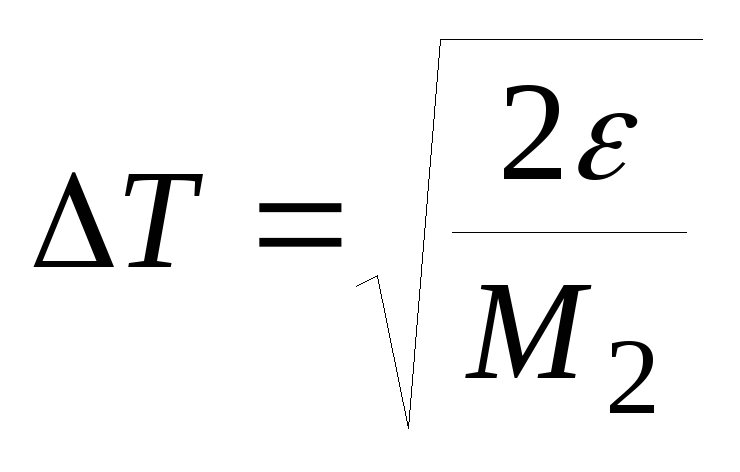

   Вновь используем неравенство Бернштейна (23):

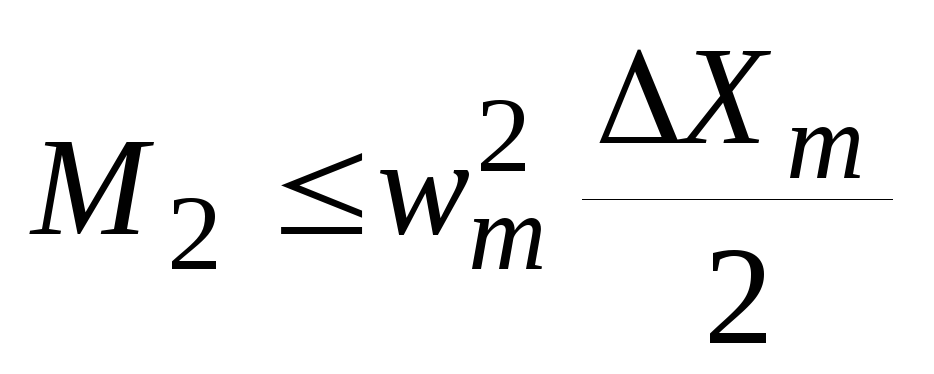   , тогда

   (31).

   где - нормированная погрешность восстановления.

   С учетом (14), где w_m=1,46ba

   (32)

   т.е. шаг при линейной интерполяции в 2 раза больше шага при линейной экстрополяции.

   3.2. Среднеквадратический показатель точности дискретизации.

   При экстрополяции полиномом нулевой степени, поскольку оценка сигнала 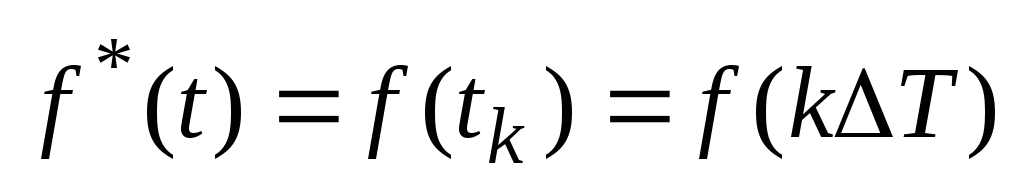не отличается от оценки при интерполяционном восстановлении, шаг дискретизации оценивается аналогично(см.п.2.2.1.)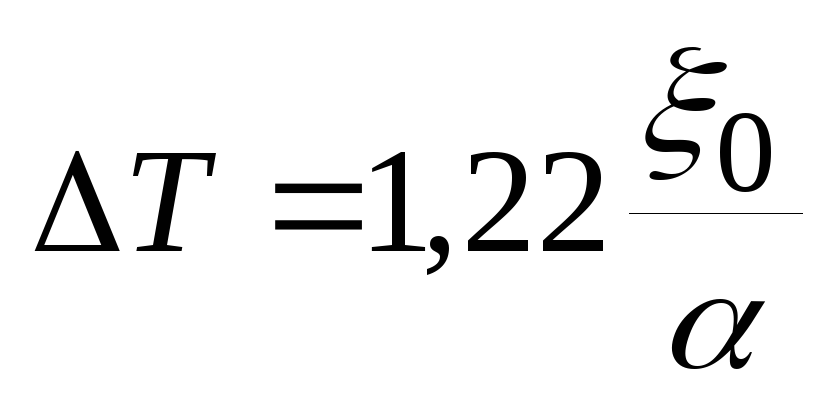

   

   При линейной экстрополяции для шага дискретизации в приводится выражение:(для однократно дифференцируемого сигнала)

   

   и т.к. для заданного сигнала , оценить шаг дискретизации не удается.

   4. Определение шага дискретизации при восстановлении сигнала по теореме Котельникова.

   Теорема Котельникова утверждает, что сигнал, описываемый функцией f(t) с ограниченным спектром, полностью определяется последовательностью своих значений, взятых через моменты времени

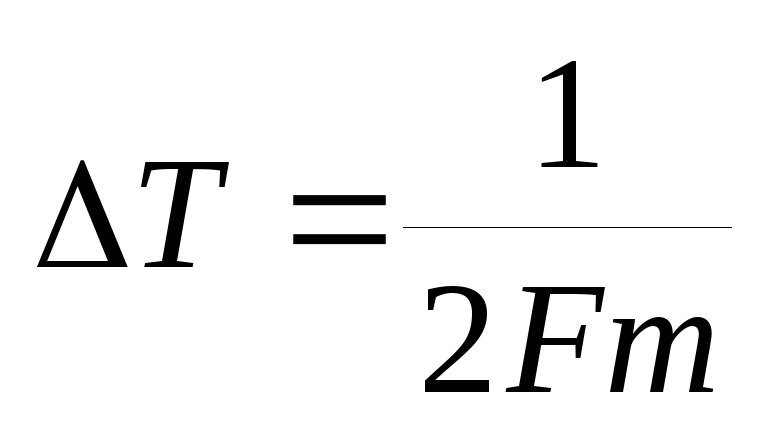   (33)

   где Fm – ширина спектра сигнала.

   При этом

   

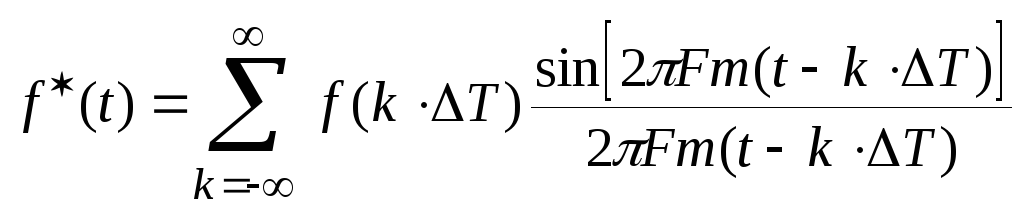
   Из (14) w_m=1,46ba

   т.е.

   Тогда необходимый шаг дискретизации:

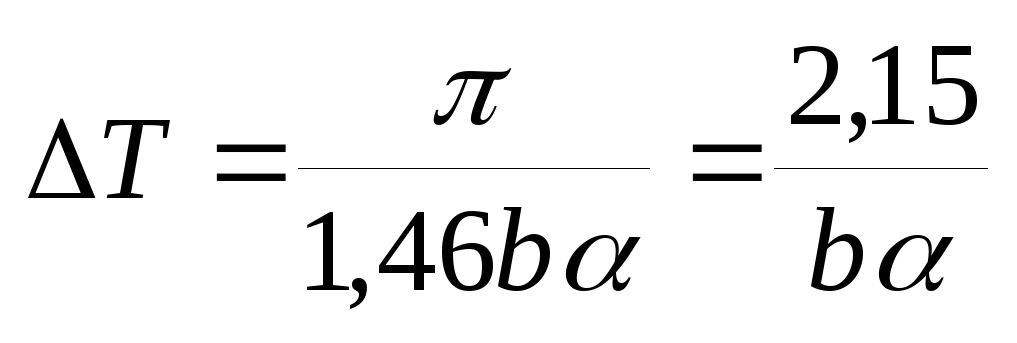   (34)

   При восстановлении сигнала по теореме Котельникова необходимыми условиями являются:

3. ограниченный спектр сигнала (верхняя частота спектра Fm)

4. неограниченная длительность сигнала

При этих условиях восстановление сигнала происходит безошибочно , если шаг дискретизации выбран как . Выбор другого шага бедет противоречить теореме Котельникова. Т.к. заданный сигнал имеет ограниченный спектр (см.п.1.), то предпологая, что его длительность бесконечна, шаг дискретизации определяется из (34).