
- •Джиргалова с.Б., Киреева о.В., Тугульчиева в.С.
- •Лабораторная работа №1 Первообразная. Неопределенный интеграл.
- •Лабораторная работа №2 Методы интегрирования (Замена переменной. Интегрирование по частям.)
- •Замена переменной.
- •Интегрирование по частям.
- •1)Обычно в интегралах вида
- •3) Интегралы вида
- •Варианты
- •Лабораторная работа №3 Интегрирование рациональных выражений. Метод неопределенных коэффициентов.
- •Лабораторная работа № 4 Интегрирование рациональных дробей. Метод Остроградского.
- •1. В чем заключается метод Остроградского и когда им пользуются? лабораторная работа №5 Интегрирование тригонометрических функций.
- •Варианты
- •Лабораторная работа №6 Интегрирование некоторых выражений, содержащих радикалы
- •Интегрирование выражений вида
- •Интегрирование биноминальных дифференциалов.
- •III. Интегрирование выражений вида . Подстановки Эйлера.
- •Лабораторная работа №7 Определенный интеграл. Свойства определенного интеграла. Вычисление определенных интегралов.
- •Варианты
- •Лабораторная работа №8. Замена переменной в определенном интеграле и интегрирование по частям.
- •Интегрирование по частям в определенном интеграле.
- •Варианты
- •Лабораторная работа №9. Геометрические приложения определенного интеграла . Площадь плоской фигуры.
- •Лабораторная работа №10 Геометрические приложения определенного интеграла. Длина дуги кривой.
- •Литература:
Лабораторная работа №9. Геометрические приложения определенного интеграла . Площадь плоской фигуры.
Площадь
фигуры, ограниченной графиком непрерывной
функции
![]() =
,
(
0),
двумя прямыми
=
,
=
и осью OX
, или площадь криво-линейной трапеции,
ограниченной дугой графика функции
=
,
=
,
(
0),
двумя прямыми
=
,
=
и осью OX
, или площадь криво-линейной трапеции,
ограниченной дугой графика функции
=
,
![]() в (рис.1), вычисляется по формуле :
в (рис.1), вычисляется по формуле :
![]() (1)
(1)
 рис
1.
рис
1.
Площадь
фигуры , ограниченной графиками
непрерывных функции
![]() и
и
![]()
![]() и двумя прямыми
=
,
=
(рис.2), определяется по формуле :
и двумя прямыми
=
,
=
(рис.2), определяется по формуле :
![]() (2)
(2)

 рис.
2
рис.
2
Пример1.
Найти площадь фигуры, лежащей в правой
полуплоскости и ограниченной окружностью![]() и параболой
и параболой
![]()
Решение:
найдем
точки пересечения кривых ( рис.3), решив
систему уравнений :![]()
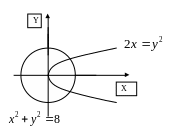 рис.
3
рис.
3
Используя
симметрию относительно оси OX
, найдем искомую площадь как удвоенную
сумму площадей криволинейных трапеций
,ограниченных соответственно дугами
параболы
,
0x2
и окружностью.![]()
S=
=![]()
Иногда удобно использовать формулы , аналогичные (1) и (2) , но по переменной (считая x функцией от ), в частности
![]() (3)
(3)
Если
фигура ограничена кривой, имеющей
параметрические уравнения
=
![]() ,
=
,
прямыми
=
,
=
и осью OX,
то площадь вычисляется по формуле :
,
=
,
прямыми
=
,
=
и осью OX,
то площадь вычисляется по формуле :
 (4),
(4),
где
пределы интегрирование находятся из
уравнений
![]() на
отрезке
на
отрезке
![]() .
.
Формула
(4) применима также для вычисления площади
фигуры, ограниченной замкнутой кривой
( изменения параметра t
от
![]() до
до
![]() должно
соответствовать обходу контура по
часовой стрелке).
должно
соответствовать обходу контура по
часовой стрелке).
Пример2.
Найти площадь петли кривой![]()
Решение:
Найдем точки пересечения кривой с
координатами осями. Имеем : x=0
при t=![]() ;
y=0
при t=0,
t=
;
y=0
при t=0,
t=![]() .Следовательно,
получаем следующие точки:
.Следовательно,
получаем следующие точки:
![]() при
t=1;
при
t=1;
![]() при t=-1;
при t=-1;
![]() при
t=0;
при
t=0;
![]() при t=
.
при t=
.
Точка
является точкой самопересечения кривой.
При
![]()
При
![]() (рис.4).
(рис.4).
График
функции
![]() ;
;
![]() ,
,
![]() при
при
![]()

Площадь фигуры находим как удвоенную площадь верхней ее половины:
![]() Площадь
фигуры, ограниченной графиком непрерывной
функции
Площадь
фигуры, ограниченной графиком непрерывной
функции
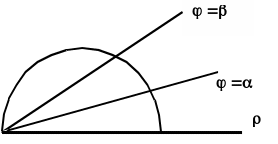
![]() и двумя лучами
и двумя лучами
![]() где
где
![]() - полярные координаты, или площадь
криволинейного сектора , ограниченного
дугой графика функции
,
- полярные координаты, или площадь
криволинейного сектора , ограниченного
дугой графика функции
,
![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]() (5).
(5).
Пример
3. Найти площадь лунки , ограниченной
дугами окружностей
![]() Окружности пересекаются при
Окружности пересекаются при
![]() ;
рассматриваемая фигура ( рис.5) симметрична
относительно луча
.
;
рассматриваемая фигура ( рис.5) симметрична
относительно луча
.
График
функции
![]() ;
;
![]() ,
,
![]() при
при
![]()
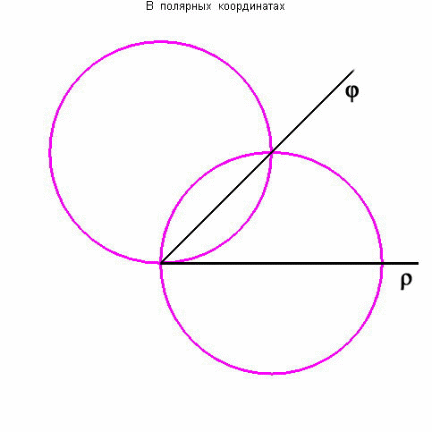
Следовательно,
ее площадь можно вычислять так:
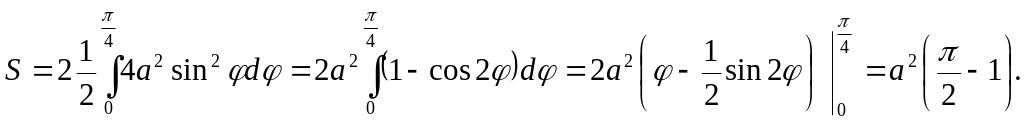
ВАРИАНТЫ
Вычислить площадь фигуры, ограниченной данными линиями:
В-1.
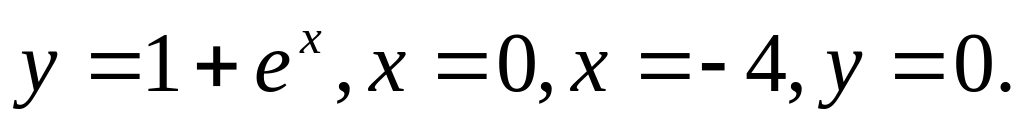
 и
ее асимптотой.
и
ее асимптотой.Кардиоидой
 .
.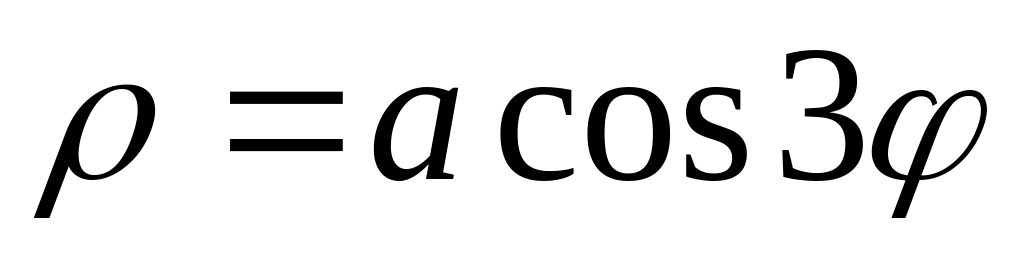 .
.
В-5.
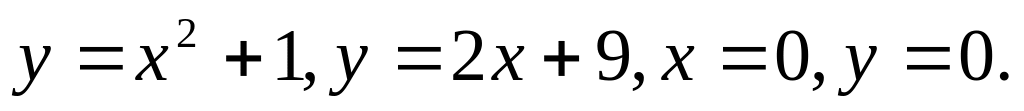
 и
касательные к ней , проведенные через
токи
и
касательные к ней , проведенные через
токи
одной аркой циклиды


В-3.

 касательной
к ней в точке
касательной
к ней в точке
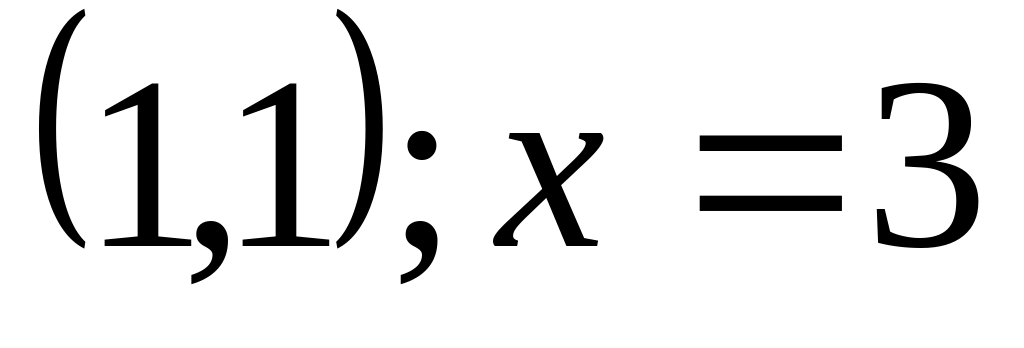 и осью OX.
и осью OX.Астроидой

 (
Бернулли ) .
(
Бернулли ) .
В-4.
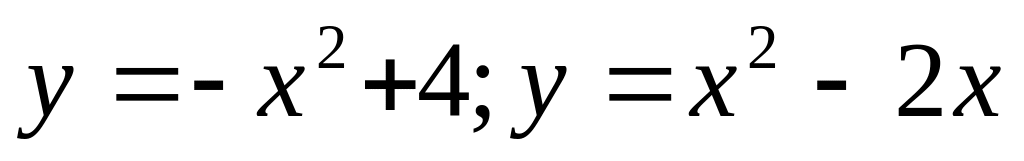
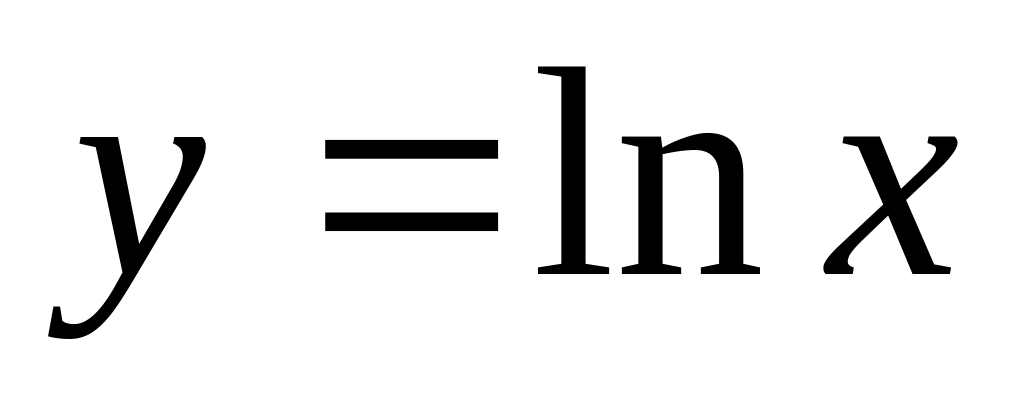 ,
касательной к ней в точке x=e
и осью OX.
,
касательной к ней в точке x=e
и осью OX.Петли линии
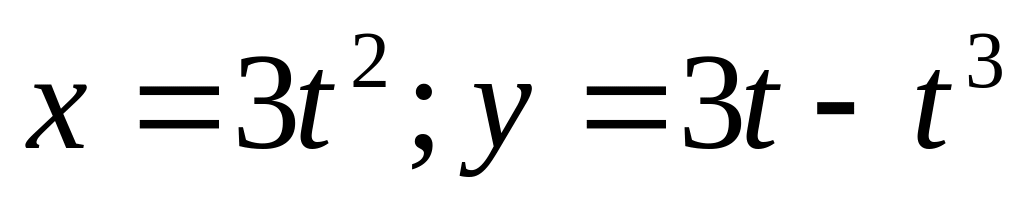 .
.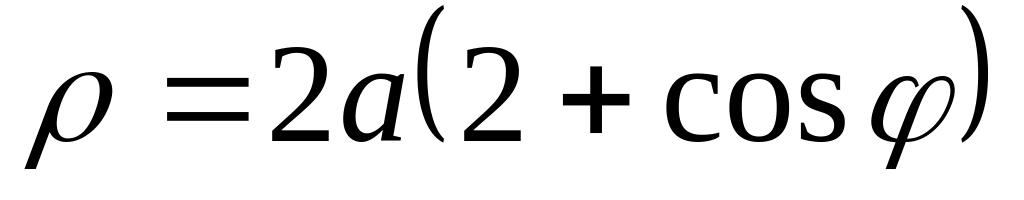 (
улитка Паскаля )
(
улитка Паскаля )
В-5.
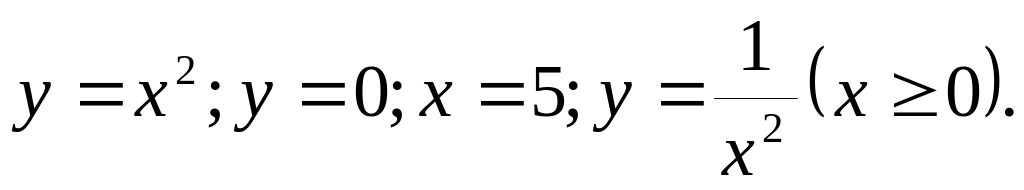
 ,
касательной к ней в точке
,
касательной к ней в точке
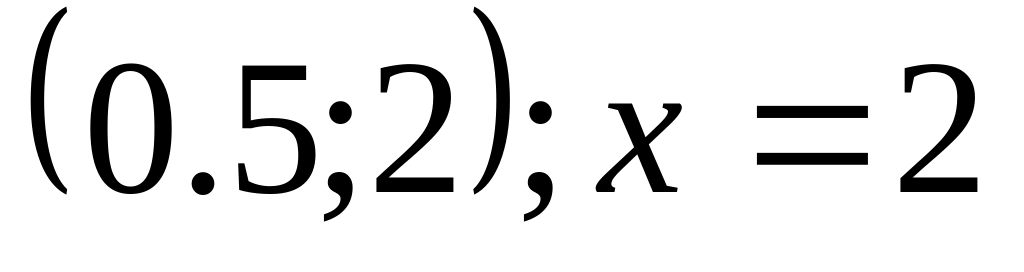 .
.Одной арки циклоиды
 и OX.
и OX.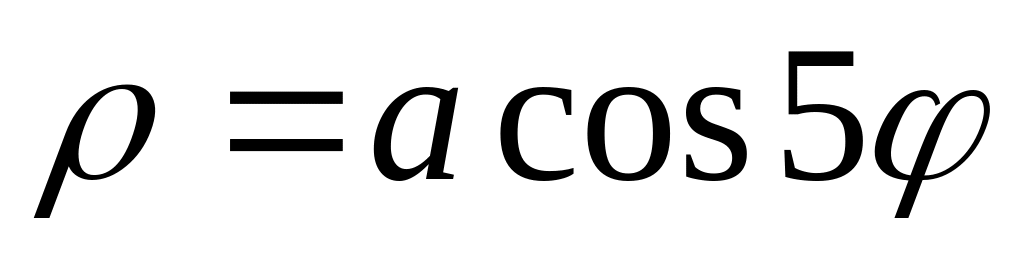 .
.
В-6.
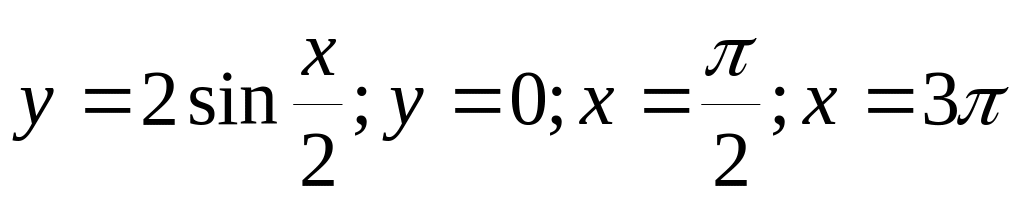
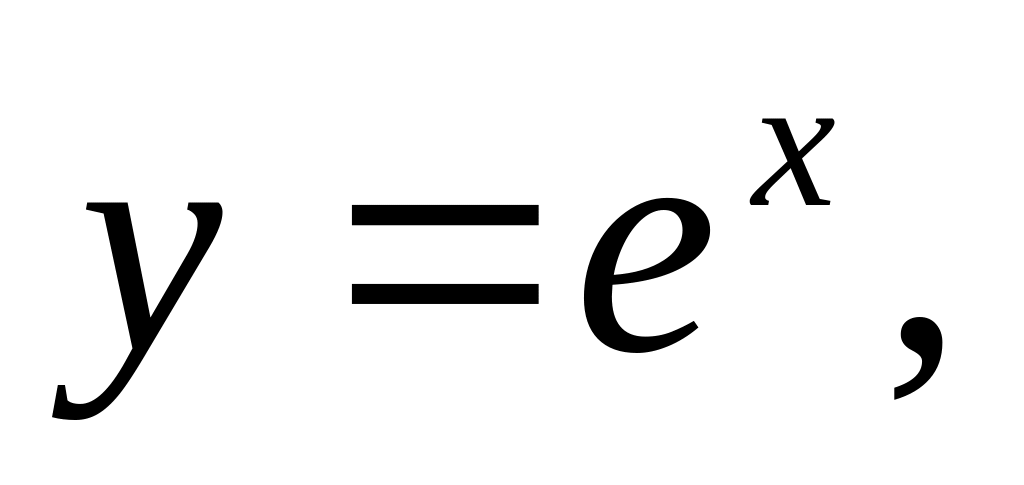 касательной
к ней в точке
касательной
к ней в точке
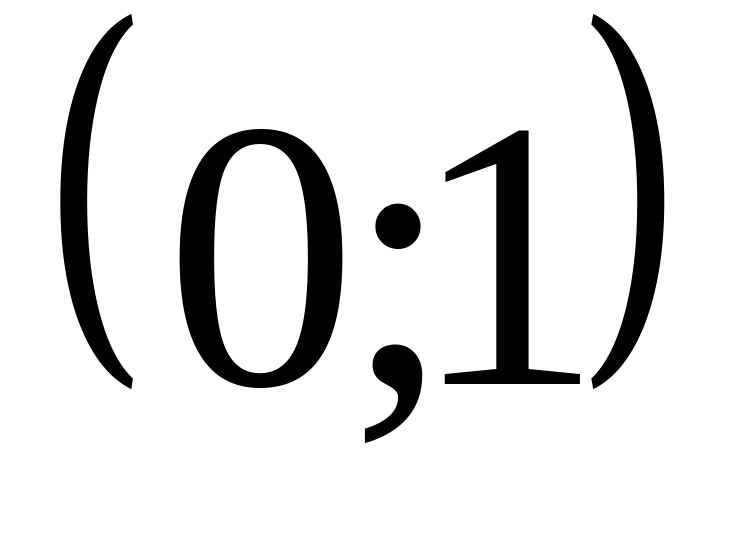 и x=1.
и x=1.Петли линии
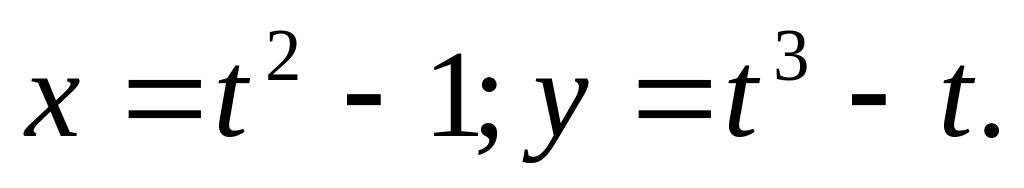
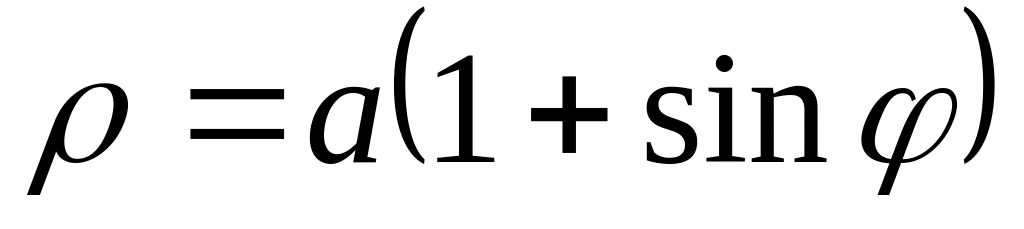 (кардиоида)
(кардиоида)
В-7.

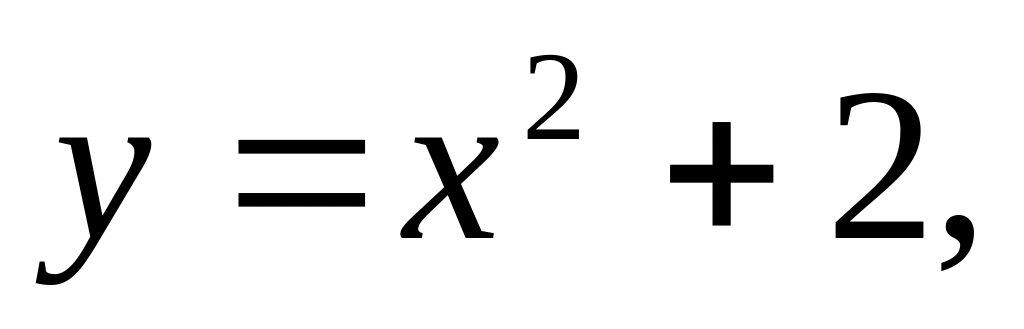 касательной
к ней в точке M
касательной
к ней в точке M к осью ординат.
к осью ординат.Петли кривой
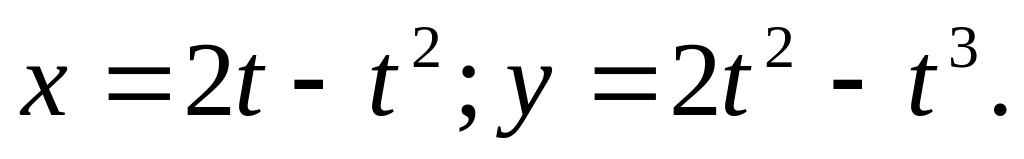
 (
лепестковая роза).
(
лепестковая роза).
В-8.
Параболой
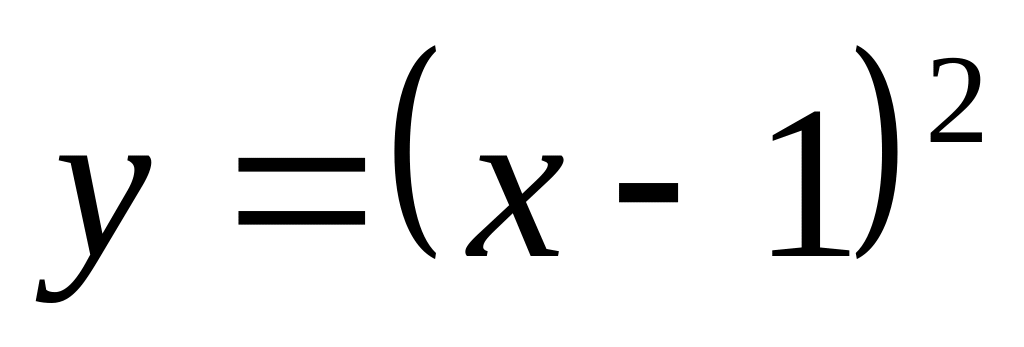 и гиперболой
и гиперболой
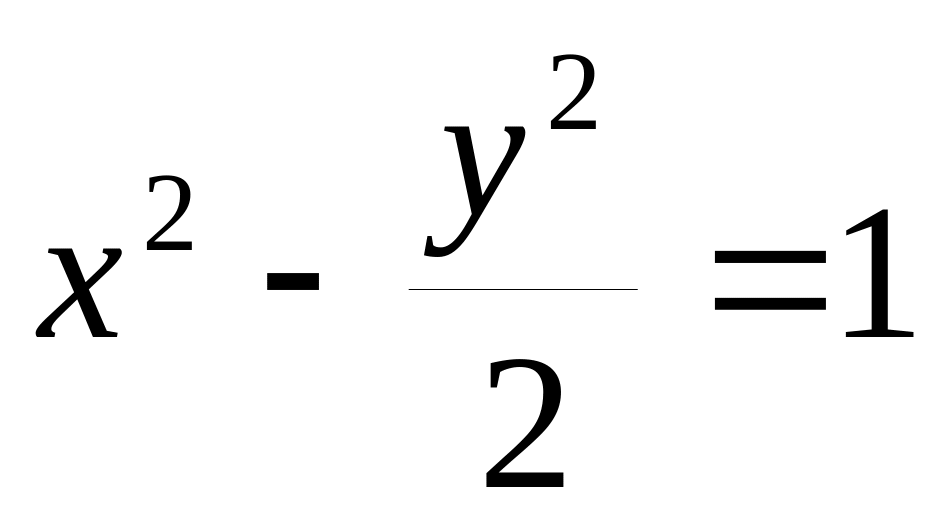


 (в
не круга
(в
не круга
 )
)
В-9
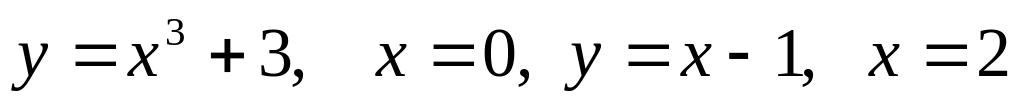
Найдите площадь фигуры, ограниченной графиком функции
 и касательными к этому графику,
проведенными через точку
и касательными к этому графику,
проведенными через точку
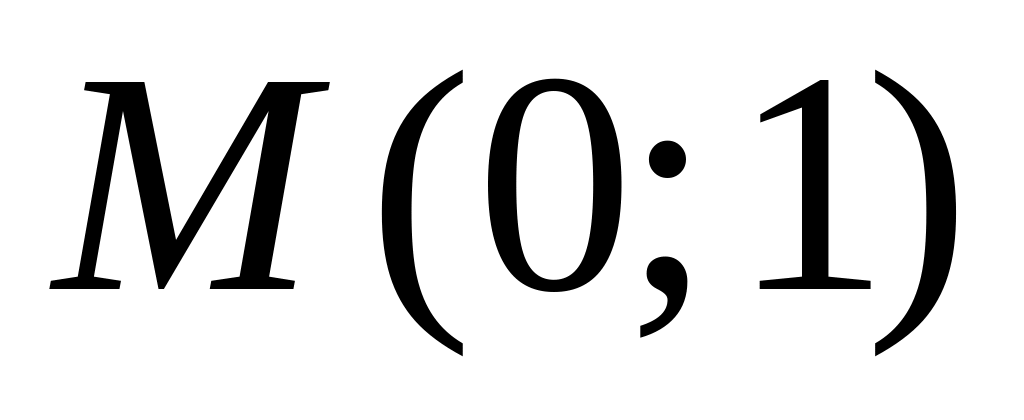 .
.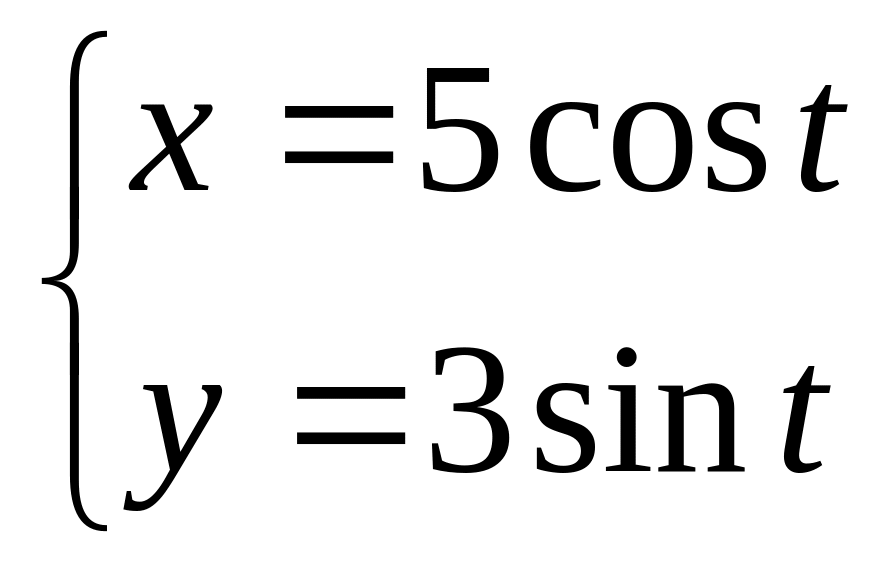
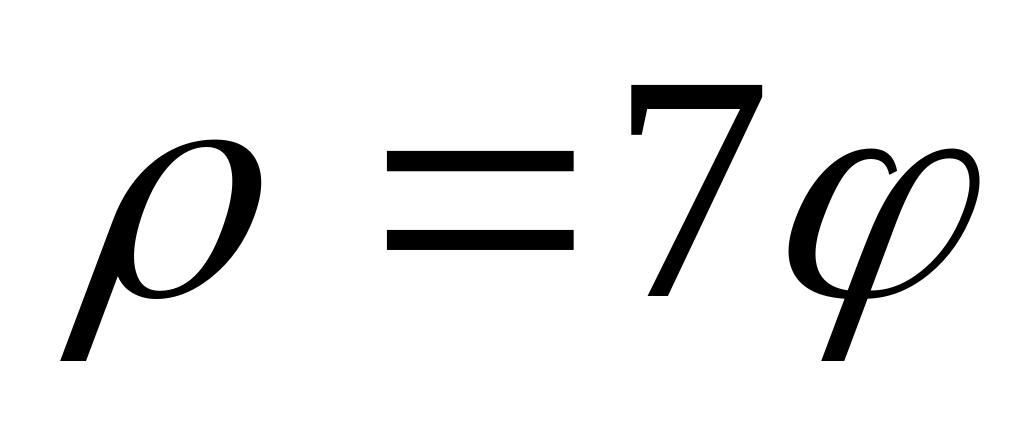
В-10
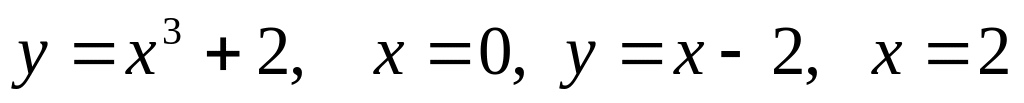
Найдите площадь фигуры, ограниченной графиком функции
 и касательными к этому графику,
проведенными через точку
и касательными к этому графику,
проведенными через точку
 .
.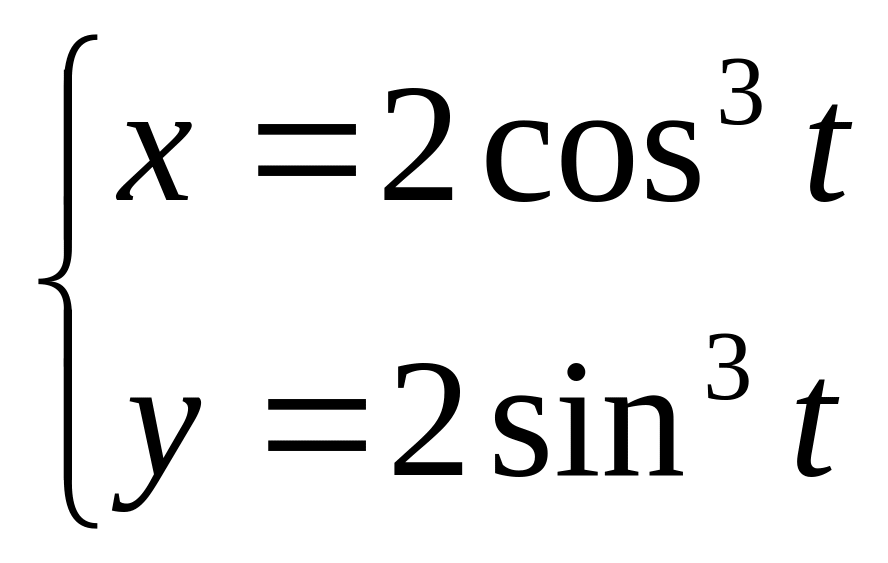

В-11

Найдите площадь фигуры, ограниченной графиками функций
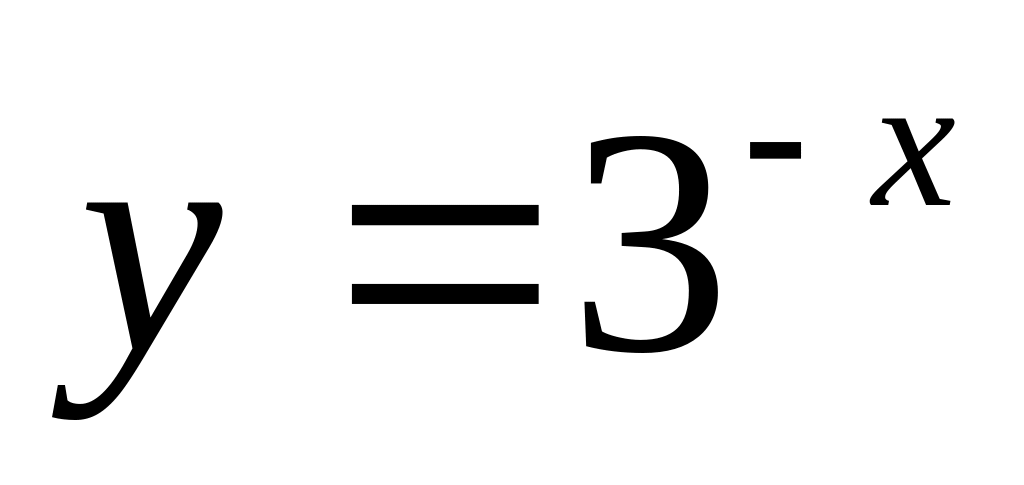 ,
,
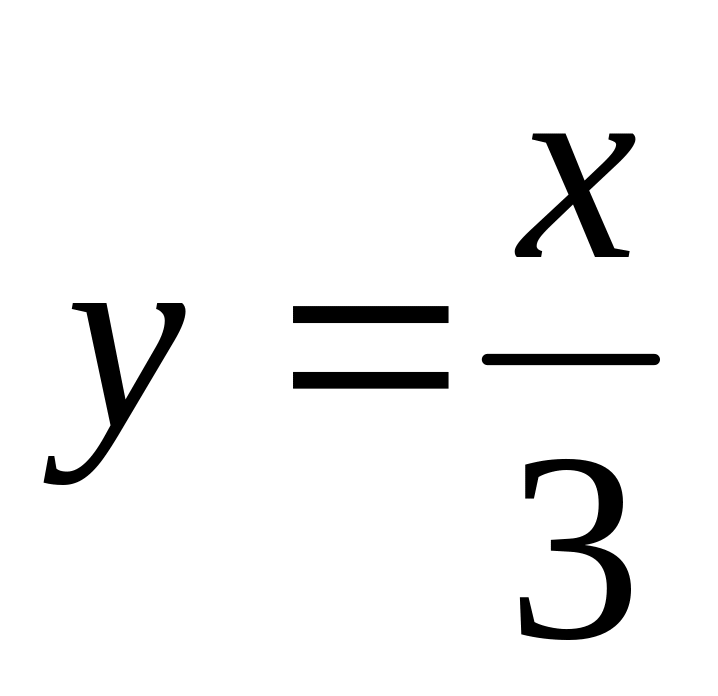 и осью ординат.
и осью ординат.

В-12
2)
![]()
3)
![]()
4)
![]()
В-13
В-14
В-15
В-16
В-17
1)
![]()
В-18
1)
![]()
В-19
В-20
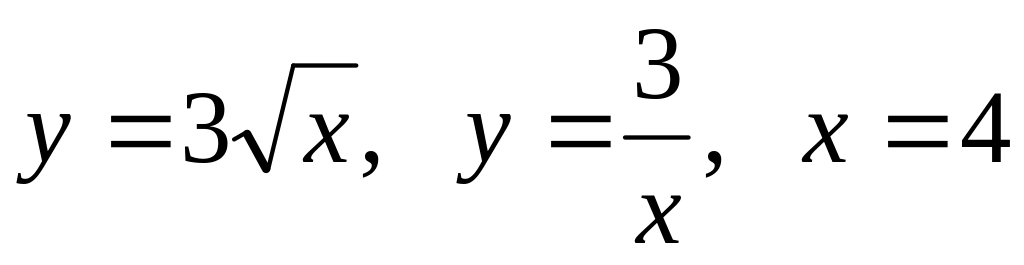

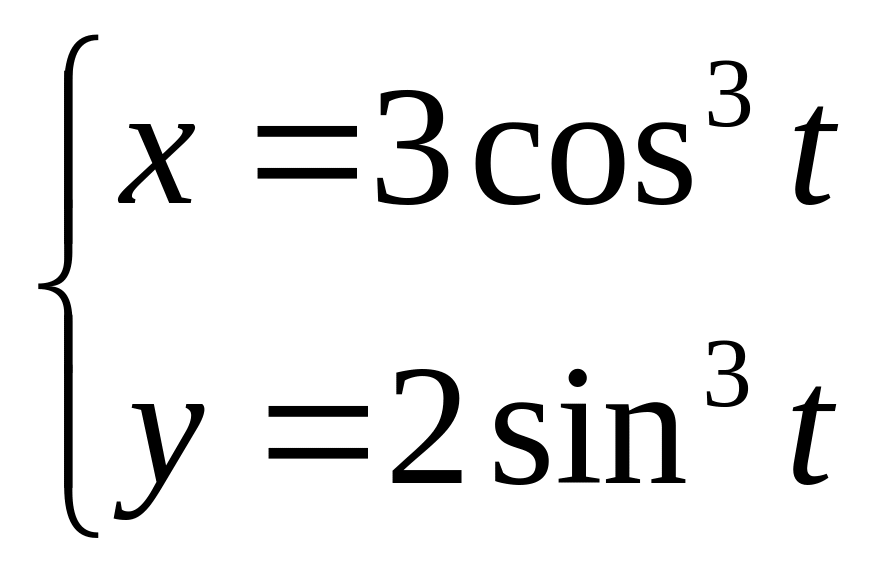
площадь, ограниченную кардиоидой
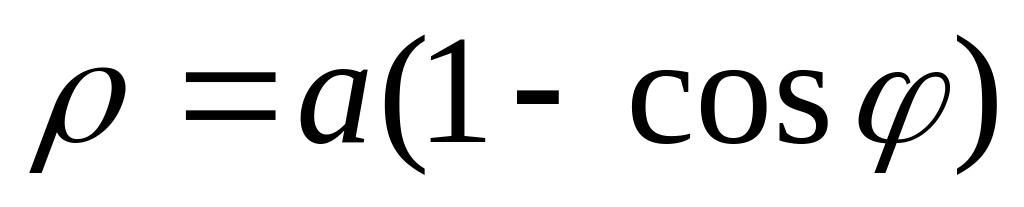 и окружностью
и окружностью
 .
.
В-21
В-22

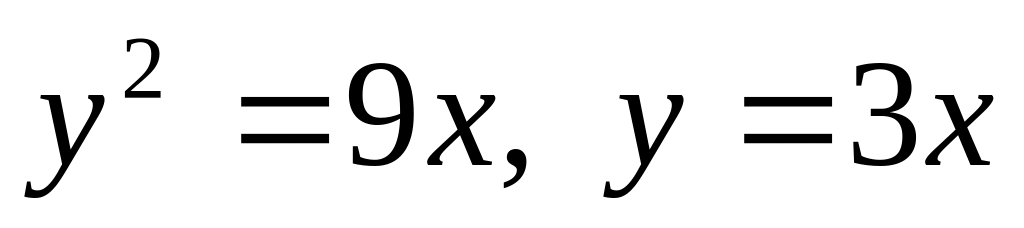
одной петлей кривой
![]()
4)
![]() (общая область)
(общая область)
В-23
В-24
В-25

Вычислить площадь, ограниченную параболой
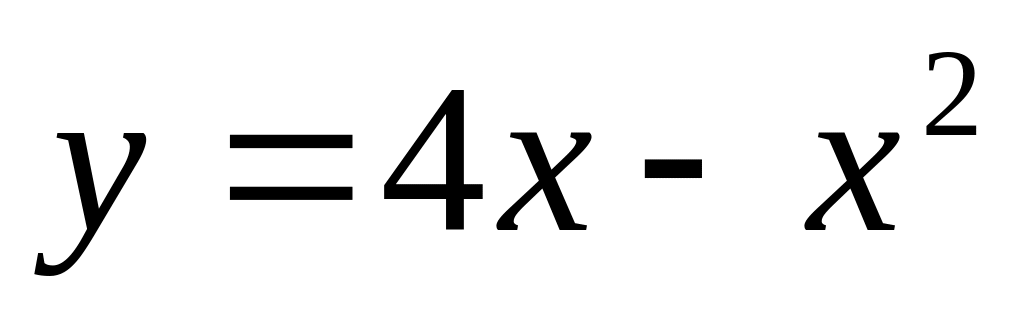 и осью абсцисс.
и осью абсцисс.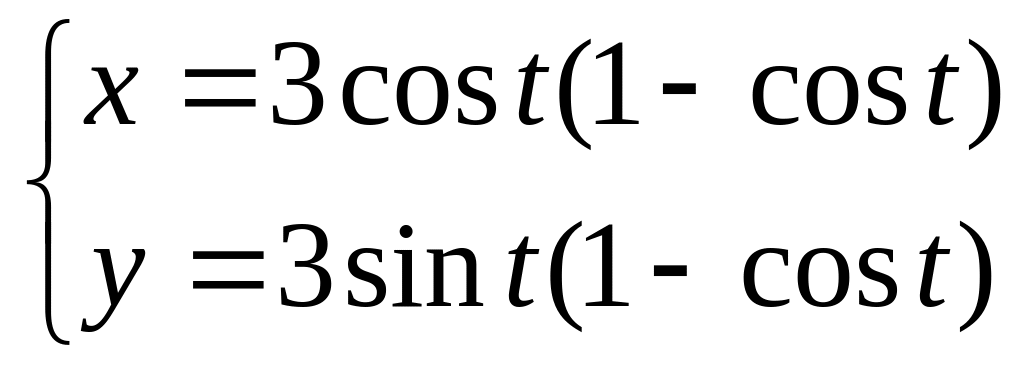
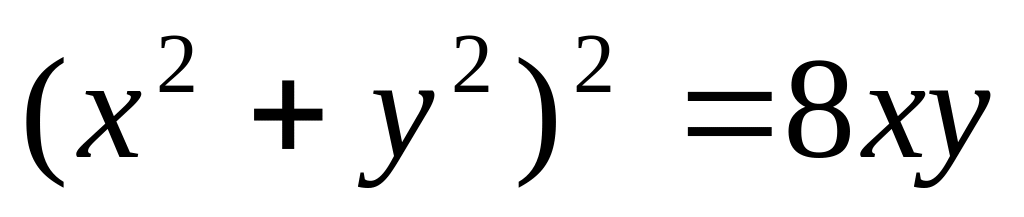
Вопросы к лабораторной работе №9:
Какая фигура называется квадрируемой? Какие вы знаете условия квадрируемости?
Какими свойствами обладает квадрируемая фигура?
Как вычисляется площадь плоской фигуры, ограниченной прямыми
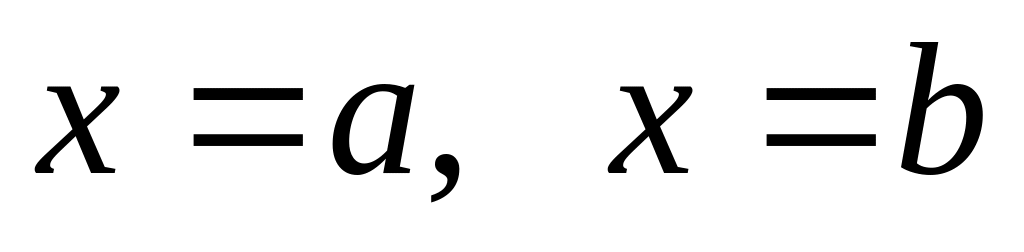 и непрерывными кривыми
и непрерывными кривыми
 и
и
 ,
при условии, что
,
при условии, что
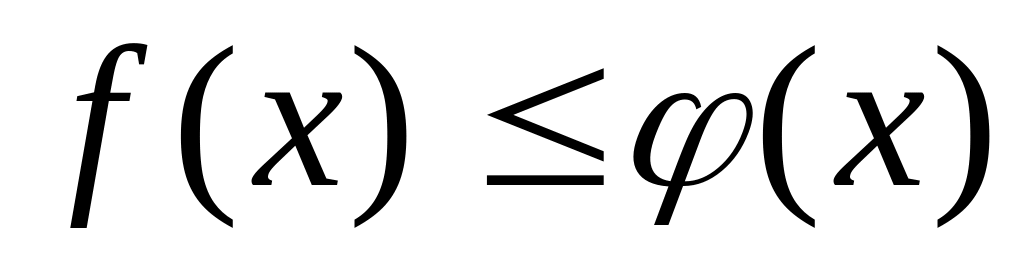 для
для
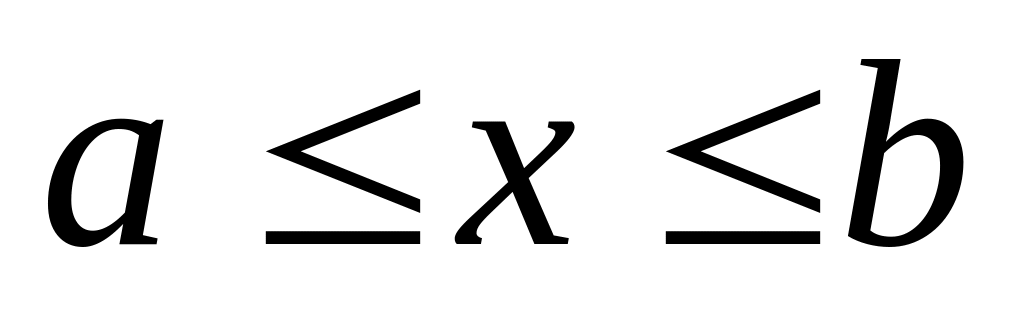 ?
?
